Question
Two players, A and B, alternately throw a fair six-sided dice, with A starting, until one of them obtains a six. Find the probability that A obtains the first six.
▶️Answer/Explanation
Markscheme
P(six in first throw) \( = \frac{1}{6}\) (A1)
P(six in third throw) \( = \frac{{25}}{{36}} \times \frac{1}{6}\) (M1)(A1)
P(six in fifth throw)\( = {\left( {\frac{{25}}{{36}}} \right)^2} \times \frac{1}{6}\)
P(A obtains first six) \( = \frac{1}{6} + \frac{{25}}{{36}} \times \frac{1}{6} + {\left( {\frac{{25}}{{36}}} \right)^2} \times \frac{1}{6} + \ldots \) (M1)
recognizing that the common ratio is \({\frac{{25}}{{36}}}\) (A1)
P(A obtains first six) \( = \frac{{\frac{1}{6}}}{{1 – \frac{{25}}{{36}}}}\,\,\,\,\,\)(by summing the infinite GP) M1
\( = \frac{6}{{11}}\) A1
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
a.Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.[4]
b.Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) . [3]
▶️Answer/Explanation
Markscheme
a.(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1 [3 marks]
Question
In a population of rabbits, \(1\%\) are known to have a particular disease. A test is developed for the disease that gives a positive result for a rabbit that does have the disease in \(99\%\) of cases. It is also known that the test gives a positive result for a rabbit that does not have the disease in \(0.1\%\) of cases. A rabbit is chosen at random from the population.
a. Find the probability that the rabbit tests positive for the disease.[2]
b. Given that the rabbit tests positive for the disease, show that the probability that the rabbit does not have the disease is less than 10 %. [3]
▶️Answer/Explanation
Markscheme
a. R is ‘rabbit with the disease’
P is ‘rabbit testing positive for the disease’
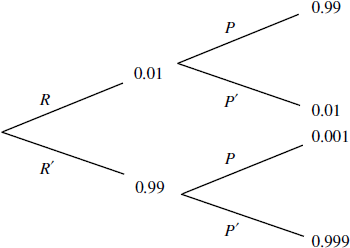
\({\text{P}}(P) = P(R \cap P) + P(R’ \cap P)\)
\( = 0.01 \times 0.99 + 0.99 \times 0.001\) M1
\( = 0.01089( = 0.0109)\) A1
Note: Award M1 for a correct tree diagram with correct probability values shown.
[2 marks]
R is ‘rabbit with the disease’
P is ‘rabbit testing positive for the disease’
\(P(R’|P) = \frac{{0.001 \times 0.99}}{{0.001 \times 0.99 + 0.01 \times 0.99}}\left( { = \frac{{0.00099}}{{0.01089}}} \right)\) M1A1
\(\frac{{0.00099}}{{0.01089}} < \frac{{0.001}}{{0.01}} = 10\% \) (or other valid argument) R1
[3 marks]
Question
A batch of 15 DVD players contains 4 that are defective. The DVD players are selected at random, one by one, and examined. The ones that are checked are not replaced.
a.What is the probability that there are exactly 3 defective DVD players in the first 8 DVD players examined?[4]
b.What is the probability that the \({9^{{\text{th}}}}\) DVD player examined is the \({4^{{\text{th}}}}\) defective one found? [3]
▶️Answer/Explanation
Markscheme
METHOD 1
P(3 defective in first 8) \(=\left( {\begin{array}{*{20}{c}}
8 \\
3
\end{array}} \right) \times \frac{4}{{15}} \times \frac{3}{{14}} \times \frac{2}{{13}} \times \frac{{11}}{{12}} \times \frac{{10}}{{11}} \times \frac{9}{{10}} \times \frac{8}{9} \times \frac{7}{8}\) M1A1A1
Note: Award M1 for multiplication of probabilities with decreasing denominators.
Award A1 for multiplication of correct eight probabilities.
Award A1 for multiplying by \(\left( {\begin{array}{*{20}{c}}
8 \\
3
\end{array}} \right)\).
\( = \frac{{56}}{{195}}\) A1
METHOD 2
a.P(3 defective DVD players from 8) \( = \frac{{\left( {\begin{array}{*{20}{c}}
4 \\
3
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{11} \\
5
\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}
{15} \\
8
\end{array}} \right)}}\) M1A1
Note: Award M1 for an expression of this form containing three combinations.
\( = \frac{{\frac{{4!}}{{3!1!}} \times \frac{{11!}}{{5!6!}}}}{{\frac{{15!}}{{8!7!}}}}\) M1
\( = \frac{{56}}{{195}}\) A1
[4 marks]
\({\text{P(}}{{\text{9}}^{{\text{th}}}}{\text{ selected is }}{{\text{4}}^{{\text{th}}}}{\text{ defective player}}|{\text{3 defective in first 8)}} = \frac{1}{7}\) (A1)
\({\text{P(}}{{\text{9}}^{{\text{th}}}}{\text{ selected is }}{{\text{4}}^{{\text{th}}}}{\text{ defective player)}} = \frac{{56}}{{195}} \times \frac{1}{7}\) M1
\( = \frac{8}{{195}}\) A1
[3 marks]
Question
A batch of 15 DVD players contains 4 that are defective. The DVD players are selected at random, one by one, and examined. The ones that are checked are not replaced.
a. What is the probability that there are exactly 3 defective DVD players in the first 8 DVD players examined?[4]
b.What is the probability that the \({9^{{\text{th}}}}\) DVD player examined is the \({4^{{\text{th}}}}\) defective one found? [3]
▶️Answer/Explanation
Markscheme
METHOD 1
P(3 defective in first 8) \(=\left( {\begin{array}{*{20}{c}}
8 \\
3
\end{array}} \right) \times \frac{4}{{15}} \times \frac{3}{{14}} \times \frac{2}{{13}} \times \frac{{11}}{{12}} \times \frac{{10}}{{11}} \times \frac{9}{{10}} \times \frac{8}{9} \times \frac{7}{8}\) M1A1A1
Note: Award M1 for multiplication of probabilities with decreasing denominators.
Award A1 for multiplication of correct eight probabilities.
Award A1 for multiplying by \(\left( {\begin{array}{*{20}{c}}
8 \\
3
\end{array}} \right)\).
\( = \frac{{56}}{{195}}\) A1
METHOD 2
a.P(3 defective DVD players from 8) \( = \frac{{\left( {\begin{array}{*{20}{c}}
4 \\
3
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{11} \\
5
\end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}}
{15} \\
8
\end{array}} \right)}}\) M1A1
Note: Award M1 for an expression of this form containing three combinations.
\( = \frac{{\frac{{4!}}{{3!1!}} \times \frac{{11!}}{{5!6!}}}}{{\frac{{15!}}{{8!7!}}}}\) M1
\( = \frac{{56}}{{195}}\) A1
[4 marks]
\({\text{P(}}{{\text{9}}^{{\text{th}}}}{\text{ selected is }}{{\text{4}}^{{\text{th}}}}{\text{ defective player}}|{\text{3 defective in first 8)}} = \frac{1}{7}\) (A1)
\({\text{P(}}{{\text{9}}^{{\text{th}}}}{\text{ selected is }}{{\text{4}}^{{\text{th}}}}{\text{ defective player)}} = \frac{{56}}{{195}} \times \frac{1}{7}\) M1
\( = \frac{8}{{195}}\) A1
[3 marks]
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
a.Draw a tree diagram to represent these events and their outcomes.[1]
b.What is the probability that the “Tigers” soccer team wins?[2]
c.Given that the “Tigers” soccer team won, what is the probability that it rained on that day?[2]
▶️Answer/Explanation
Markscheme (a).
let R be “it rains” and W be “the ‘Tigers’ soccer team win”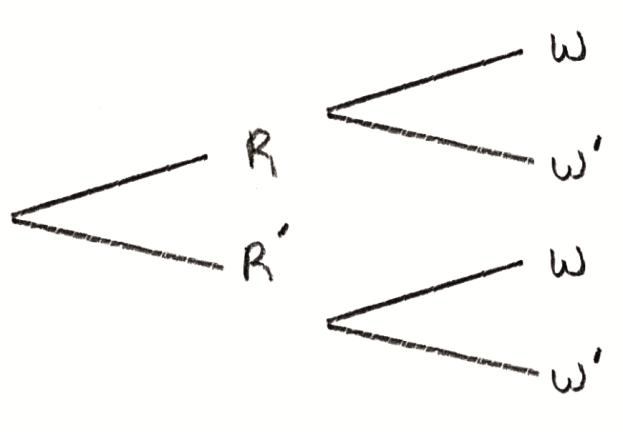
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Question
Mobile phone batteries are produced by two machines. Machine A produces 60% of the daily output and machine B produces 40%. It is found by testing that on average 2% of batteries produced by machine A are faulty and 1% of batteries produced by machine B are faulty.
a.(i) Draw a tree diagram clearly showing the respective probabilities.
(ii) A battery is selected at random. Find the probability that it is faulty.
(iii) A battery is selected at random and found to be faulty. Find the probability that it was produced by machine A. [6]
In a pack of seven transistors, three are found to be defective. Three transistors are selected from the pack at random without replacement. The discrete random variable X represents the number of defective transistors selected.
b.(i) Find \({\text{P}}(X = 2)\).
(ii) Copy and complete the following table:
(iii) Determine \({\text{E}}(X)\). [6]
▶️Answer/Explanation
Markscheme
a.(i)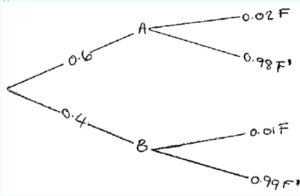
A1A1
Note: Award A1 for a correctly labelled tree diagram and A1 for correct probabilities.
(ii) \({\text{P}}(F) = 0.6 \times 0.02 + 0.4 \times 0.01\) (M1)
\( = 0.016\) A1
(iii) \({\text{P}}(A|F) = \frac{{{\text{P}}(A \cap F)}}{{{\text{P}}(F)}}\)
\( = \frac{{0.6 \times 0.02}}{{0.016}}{\text{ }}\left( { = \frac{{0.012}}{{0.016}}} \right)\) M1
\( = 0.75\) A1
[6 marks]
(i) METHOD 1
\({\text{P}}(X = 2) = \frac{{^3{C_2}{ \times ^4}{C_1}}}{{^7{C_3}}}\) (M1)
\( = \frac{{12}}{{35}}\) A1
METHOD 2
\(\frac{3}{7} \times \frac{2}{6} \times \frac{4}{5} \times 3\) (M1)
\( = \frac{{12}}{{35}}\) A1
(ii) 
A2
Note: Award A1 if \(\frac{4}{{35}},{\text{ }}\frac{{18}}{{35}}\) or \(\frac{1}{{35}}\) is obtained.
(iii) \({\text{E}}(X) = \sum {x{\text{P}}(X = x)} \)
\({\text{E}}(X) = 0 \times \frac{4}{{35}} + 1 \times \frac{{18}}{{35}} + 2 \times \frac{{12}}{{35}} + 3 \times \frac{1}{{35}}\) M1
\( = \frac{{45}}{{35}} = \left( {\frac{9}{7}} \right)\) A1
[6 marks]
Question
A bag contains three balls numbered 1, 2 and 3 respectively. Bill selects one of these balls at random and he notes the number on the selected ball. He then tosses that number of fair coins.
a.Calculate the probability that no head is obtained.[3]
b.Given that no head is obtained, find the probability that he tossed two coins.[3]
▶️Answer/Explanation
Markscheme
a.P(no heads from n coins tossed) = \({0.5^n}\) (A1)
P(no head) = \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{8}\) M1
= \(\frac{7}{{24}}\) A1
[3 marks]
\({\text{P(2 | no heads)}} = \frac{{{\text{P(2 coins and no heads)}}}}{{{\text{P(no heads)}}}}\) M1
\( = \frac{{\frac{1}{{12}}}}{{\frac{7}{{24}}}}\) A1
\( = \frac{2}{7}\) A1
[3 marks]
Question
The following Venn diagram shows the universal set \(U\) and the sets \(A\) and \(B\) together with the probabilities of the corresponding regions.
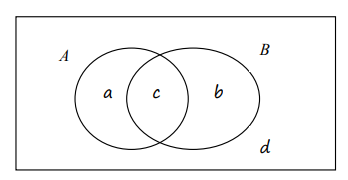
where \(a + b + c + d = 1\). Express in terms of \(a, b, c, d\) the following probabilities:
| \(P(A)\) | \(P(A|B)\) | ||
| \(P(A’)\) | \(P(B|A)\) | ||
| \(P(A\cap B)\) | \(P(A’|B)\) | ||
| \(P(A\cup B)\) | \(P(A|B’)\) | ||
| \(P(A’\cap B)\) | \(P(B’|A)\) | ||
| \(P(A’\cup B)\) | \(P(B|A’)\) | ||
| \(P(A’\cap B’)\) | \(P(A’|B’)\) | ||
| \(P(A’\cup B’)\) | \(P(B’|A’)\) |
▶️Answer/Explanation
Ans:
| \(P(A)\) | \(a+c\) | \(P(A|B)\) | \(c / (b+c)\) |
| \(P(A’)\) | \(b+d\) | \(P(B|A)\) | \(c / (a+c)\) |
| \(P(A\cap B)\) | \(c\) | \(P(A’|B)\) | \(b / (b+c)\) |
| \(P(A\cup B)\) | \(a+b+c\) | \(P(A|B’)\) | \(a / (a+d)\) |
| \(P(A’\cap B)\) | \(b\) | \(P(B’|A)\) | \(a / (a+c)\) |
| \(P(A’\cup B)\) | \(a+c+d\) | \(P(B|A’)\) | \(b / (b+d)\) |
| \(P(A’\cap B’)\) | \(d\) | \(P(A’|B’)\) | \(d / (a+d)\) |
| \(P(A’\cup B’)\) | \(a+b+d\) | \(P(B’|A’)\) |
Question
The following Venn diagram shows the universal set \(U\) and the sets \(A\) and \(B\) together with the probabilities of the corresponding regions.
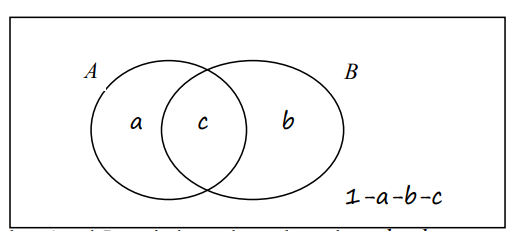
- Given that \(A\) and \(B\) are independent, show that \(ab + bc + ca = c – c^2\)
- Given that \(P(A|B) = 0.3\), show that \(3b = 7c\)
- Given that \(P(A| B’) = 0.3\), show that \(10a + 3b + 3c = 3\)
- Given that \(P(A|B) = 0.2, P(B|A) = 0.5\) and \(P(A \cup B) = 0.6\)
- Write down 3 linear equations in terms of \(a, b\) and \(c\)
- Hence find the values of \(a, b\) and \(c\)
▶️Answer/Explanation
Ans:
(a), (b), (c) proofs
d. \(a=0.1,b=0.4,c=0.1\)
Question
In a survey of 50 people it is found that 40 own a television and 21 own a computer. Four do not own either a computer or a television. A person is chosen at random from this group.
- Find the probability that this person owns both a television and a computer.
- Given that this person owns a computer, find the probability that he also owns a television.
Extra questions
Find the probability that - this person owns both a television or a computer.
- this person owns a television, given that he does not own a computer
- this person owns a computer, given that he does not own a television
▶️Answer/Explanation
Ans:
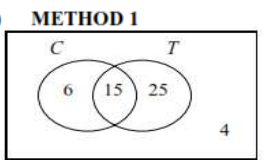
- \(P(T\cap C)=0.3\)
METHOD 2
\(n(T\cup C)=n(T)+n(C)-n(T\cap C)\)
\(46=40+21-n(T\cap C)\)
\(n(T\cap C)=15\)
\(P(T\cap C)=0.3\) - \(P(T|C)=\frac{P(T\cap C)}{P(C)}\)
\(=\frac{0.3}{0.42}(=\frac{5}{7},0.714\) to 3 s.f\()\)
Question
The events \(A\) and \(B\) are such that \(P(A) = 0.5, P(B) = 0.3, P(A \cup B) = 0.6\).
- Find the value of \(P(A \cap B)\).
- Hence show that \(A\) and \(B\) are not independent.
- Find the value of \(P(B| A)\) .
▶️Answer/Explanation
Ans:
- Use of \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)
\(0.6=0.5+0.3-P(A \cap B)\)
\(P(A \cap B)\)=\(0.2\) - \(P(A)P(B)=0.15 \ne P(A \cap B)\)
Hence not independent
- Use of \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)
- Use of \(P(B|A)=\frac{P(B \cap A)}{P(A)}\)
=\(\frac{0.2}{0.5}\)
Question
Let \(A\) and \(B\) be events such that \(P(A) = 0.6, P(A \cup B) = 0.8\) and \(P(A|B) = 0.6\). Find \(P(B)\).
▶️Answer/Explanation
Ans:
EITHER
Using \(P(A|B)= \frac{P(A \cap B)}{P(B)}\) Hence \(0.6P(B)=P(A \cap B)\)
Using \(P(A \cup B) = P(A)+P(B)-P(A \cap B)\) to obtain
\(0.8 = 0.6 + P(B) – P(A \cap B)\)
Substituting \(0.6P(B) = P(A \cap B)\) into above equation
OR
As \(P(A | B) = P(A)\) then \(A\) and \(B\) are independent events
Using \(P(A \cup B) = P(A) + P(B) – P(A) × P(B)\)
to obtain \(0.8=0.6+P(B)-0.6×P(B)\)
THEN
\(0.8=0.6+0.4P(B)\)
\(P(B)=0.5\)
Question
Let \(A\) and \(B\) be events such that \(P(A) = \frac{1}{5}, P(B|A) = \frac{1}{4}\) and \(P(A \cup B)=\frac{7}{10}\).
- Find \(P(A \cap B)\).
- Find \(P(B)\).
- Show that \(A\) and \(B\) are not independent.
▶️Answer/Explanation
Ans:
- \(P(A \cap B)=P(A)×P(B|A)\)
\(=\frac{1}{5}×\frac{1}{4}(=\frac{1}{20})\) - \(P(A \cup B)=P(A)+P(B)-(P(A \cap B)\)
⇒\(P(B)=\frac{7}{10}-\frac{1}{5}+\frac{1}{20}\)
=\(\frac{11}{20}\) - METHOD 1
\(P(B)=\frac{11}{20}\) and \(P(B|A)=\frac{1}{4}\)
\(P(B) \ne P(B|A)\)
⇒ \(A\) and \(B\) are not independent
METHOD 2
\(P(A)×P(B)=\frac{1}{5}×\frac{11}{20}=\frac{11}{100}\) and \(P(A \cap B)=\frac{1}{20}\)
\(P(A \cap B) \ne P(A)×P(B)\)
⇒ \(A\) and \(B\) are not independent
Question
Given that events \(A\) and \(B\) are independent with \(P(A \cap B) = 0.3, P(A \cap B’) = 0.3\), find \(P(A \cup B)\).
▶️Answer/Explanation
Ans:
Method 1: (Venn diagram)
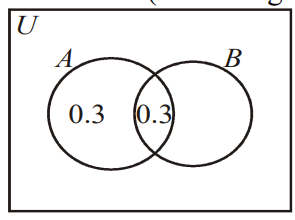
\(P(A \cap B) = P(A)P(B)\) \(0.3 = 0.6 × P(B)\)
\(P(B) = 0.5\)
Therefore, \(P(A \cup B) = 0.8\)
Method 2:
\(P(A \cap B’) = P(A) – P(A \cap B)\)
\(0.3 = P(A) – 0.3\)
\(P(A) = 0.6\)
\(P(A \cap B) = P(A)P(B)\) since \(A, B\) are independent ⇒ \(0.3 = 0.6 × P(B)\)
\(P(B) = 0.5\)
\(P(A \cup B) = P(A) + P(B) – P(A \cap B)\)
\( = 0.6 + 0.5 – 0.3= 0.8 \)
Question
The independent events \(A, B\) are such that \(P(A) = 0.4 and P(A \cup B) = 0.88\). Find
- \(P(B)\)
- the probability that either \(A\) occurs or \(B\) occurs, but not both.
▶️Answer/Explanation
Ans:
- \(0.88 = 0.4 + P(B) – 0.4P(B)\)
\(0.6P(B) = 0.48 = > P(B) = 0.8\) - METHOD 1
\(P(A \cup B) – P(A \cap B) = 0.88 – 0.32= 0.56\)
METHOD 2
\(P(A)P(B’) + P(A’)P(B) = 0.4 × 0.2 + 0.6 × 0.8= 0.56\)
Question
Given that \((A \cup B)’ = \phi, P(A’|B) = \frac{1}{3}\) and \(P(A) =\frac{6}{7}\), find \(P(B)\).
▶️Answer/Explanation
Ans:
METHOD 1
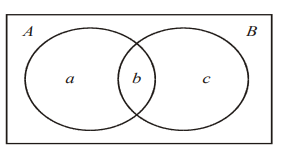
\(\frac{c}{b+c}=\frac{1}{3}\)⇒\(c=\frac{b}{2}\)
\(a+b+c=1\)⇒\(a+\frac{3}{2}b=1\)
also \(a+b=\frac{6}{7}\)
⇒\(b=\frac{2}{7}\) \(c=\frac{1}{7}\) \((a=\frac{4}{7}\) not needed\()\)
\(P(B)=b+c=\frac{3}{7}(=0.429)\)
METHOD 2
\(P(A’|B)=\frac{P(A’ \cap B)}{P(B)}\)
\(\frac{1}{3}P(B)=P(A’ \cap B)\)
\(P(A’ \cap B)+P(A)=1\)
\(\frac{1}{3}P(B)+\frac{6}{7}=1\)
\(P(B)=\frac{3}{7}\)(=0.429)
Question
Given that \(P(X) = \frac{2}{3}, P(Y |X) = \frac{2}{5}\) and \(P(Y |X’) =\frac{1}{4}\) , find
- \(P(Y’)\);
- \(P(X’ \cup Y’)\).
▶️Answer/Explanation
Ans: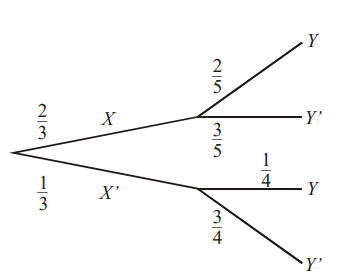 
- \(P(Y’)=\frac{2}{3}×\frac{3}{5}+\frac{1}{3}×\frac{3}{4}=\frac{13}{25}\)
- \(P(X’ \cup Y’)=1- P(X’ \cap Y’)=1-\frac{4}{15}=\frac{11}{15}\)
Question
In a bilingual school there is a class of 21 pupils. In this class, 15 of the pupils speak Spanish as their first language and 12 of these 15 pupils are Argentine. The other 6 pupils in the class speak English as their first language and 3 of these 6 pupils are Argentine. A pupil is selected at random from the class and is found to be Argentine. Find the probability that the pupil speaks Spanish as his/her first language.
METHOD A (use tree diagram)
METHOD B (use table)
| ARGENTINE | NOT ARGENTINE | TOTAL | |
| SPANISH | |||
| ENGLISH | |||
| TOTAL |
▶️Answer/Explanation
Ans:
METHOD A Using a tree diagram,
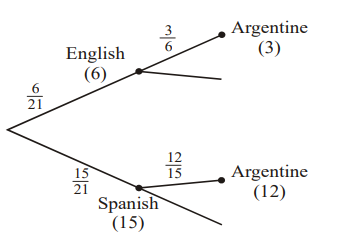
Let \(p(S)\) be the probability that the pupil speaks Spanish.
Let \(p(A)\) be the probability that the pupil is Argentine. Then, from diagram
\(p(S|A)=\frac{p(S \cap A)}{p(A)}=\frac{12}{21}/\frac{15}{21}\)
METHOD B Using a table,
| ARGENTINE | NOT ARGENTINE | TOTAL | |
| SPANISH | 12 | 3 | 15 |
| ENGLISH | 3 | 3 | 6 |
| TOTAL | 15 | 6 | 21 |
\(p(S|A)=\frac{12}{15}=\frac{4}{5}\)
Question
Box \(A\) contains 6 red balls and 2 green balls. Box \(B\) contains 4 red balls and 3 green balls. A fair cubical die with faces numbered 1,2,3,4,5,6 is thrown. If an even number is obtained, a ball is selected from box \(A\); if an odd number is obtained, a ball is selected from box \(B\).
- Calculate the probability that the ball selected was red.
- Given that the ball selected was red, calculate the probability that it came from box \(B\).
▶️Answer/Explanation
Ans:
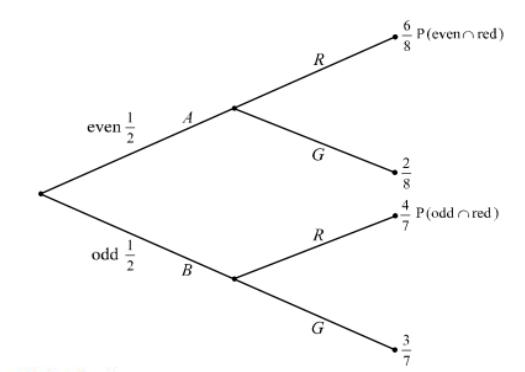
- \(P(R)=\frac{1}{2}×\frac{6}{8}+\frac{1}{2}×\frac{4}{7}\)
\(=\frac{3}{8}+\frac{2}{7}=\frac{37}{56}(0.661)\) - \(P(B|R)=\frac{P(B \cap R)}{P(R)}\)
\(=\frac{\frac{2}{7}}{\frac{37}{56}}\)
\(=\frac{16}{37}(0.432)\)
Question
A girl walks to school every day. If it is not raining, the probability that she is late is \(\frac{1}{5}\).If it is raining, the probability that she is late is \(\frac{2}{3}\). The probability that it rains on a particular day is \(\frac{1}{4}\).On one particular day the girl is late. Find the probability that it was raining on that day.
▶️Answer/Explanation
Ans:
Let \(P(R|L)\) be the probability that it is raining given that the girl is late.
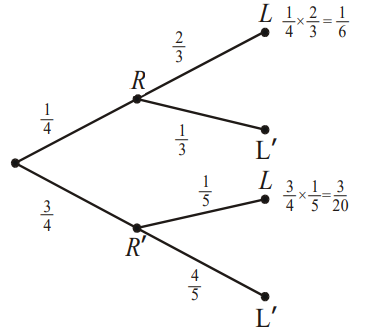
\(P(R|L)=\frac{P(R \cap L)}{P(L)}=\frac{\frac{1}{6}}{\frac{1}{6}+\frac{3}{20}}=\frac{10}{19}\)
Question
The probability that it rains during a summer’s day in a certain town is 0.2. In this town, the probability that the daily maximum temperature exceeds 25 °C is 0.3 when it rains and 0.6 when it does not rain. Given that the maximum daily temperature exceeded 25 °C on a particular summer’s day, find the probability that it rained on that day.
▶️Answer/Explanation
Ans:
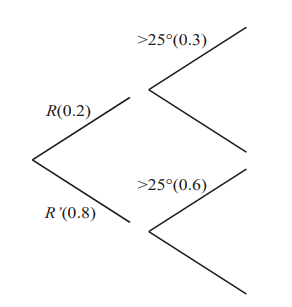
\(P(>25\)°\()=0.2×0.3+0.8×0.6=0.54\)
\(P(R|>25\)°\()=\frac{0.06}{0.54}=\frac{1}{9}(or 0.111)\)
Question
Only two international airlines fly daily into an airport. UN Air has 70 flights a day and IS Air has 65 flights a day. Passengers flying with UN Air have an 18% probability of losing their luggage and passengers flying with IS Air have a 23% probability of losing their luggage. You overhear someone in the airport complain about her luggage being lost. Find the probability that she travelled with IS Air.
▶️Answer/Explanation
Ans:
METHOD 1
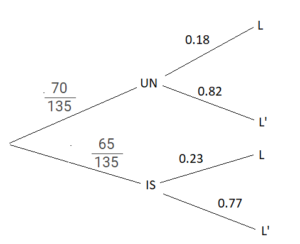
Let \(P(I)\) be the probability of flying IS Air, \(P(U)\) be the probability flying UN Air and \(P(L)\) be the probability of luggage lost.
\(P(I|L)=\frac{P(I \cap L)}{P(L)}=\frac{0.23×\frac{65}{135}}{0.18×\frac{70}{135}+0.23×\frac{65}{135}}\)
\(=\frac{299}{551}(=0.543, accept 0.542)\)
METHOD 2
Expected number of suitcases lost by UN Air is \(0.18 × 70 = 12.6\)
Expected number of suitcases lost by IS Air is \(0.23 × 65 = 14.95\)
Question
Robert travels to work by train every weekday from Monday to Friday. The probability that he catches the 08.00 train on Monday is 0.66. The probability that he catches the 08.00 train on any other weekday is 0.75. A weekday is chosen at random.
- Find the probability that he catches the train on that day.
- Given that he catches the 08.00 train on that day, find the probability that the chosen day is Monday.
▶️Answer/Explanation
Ans:
- Probability = \(0.2×0.66+0.8×0.75=0.732\)
- Probability = \(\frac{P(Mon \cap catches \space train)}{P(catches \space train)}=\frac{0.2×0.66}{0.732}=0.180 \left ( =\frac{11}{61} \right )\)
Question
A new blood test has been shown to be effective in the early detection of a disease. The probability that the blood test correctly identifies someone with this disease is 0.99, and the probability that the blood test correctly identifies someone without that disease is 0.95. The incidence of this disease in the general population is 0.0001.
A doctor administered the blood test to a patient and the test result indicated that this patient had the disease. What is the probability that the patient has the disease?
▶️Answer/Explanation
Ans:
Let \(D\) be the event that the patient has the disease and \(S\) be the event that the new blood test shows that the patient has the disease. Let \(D’\) be the complement of \(D, i.e.\) the patient does not have the disease.
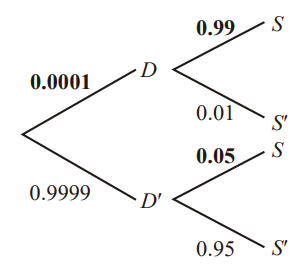
Therefore
\(p(S)= 0.0001 × 0.99 + 0.9999 × 0.05= 0.0500939\)
\(p(D|S)=\frac{0.0001 × 0.99}{0.0500939}= 0.00198 (3 s.f.)\)
Question
The probability that a man leaves his umbrella in any shop he visits is \(\frac{1}{3}\). After visiting two shops in succession, he finds he has left his umbrella in one of them. What is the probability that he left his umbrella in the second shop?
Extra Question
After visiting three shops in succession, find the probability
- that he didn’t leave the umbrella in any of them.
- that he left the umbrella in one of them.
- that he left the umbrella in the third shop, given that he left it in one of them.
▶️Answer/Explanation
Ans:
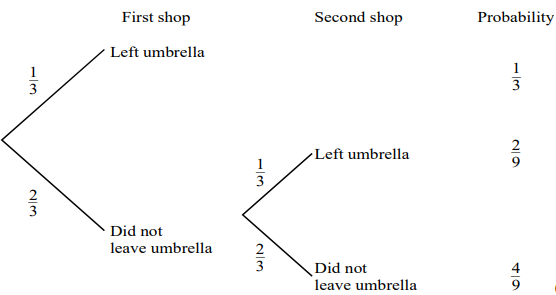
Required probability \(=\frac{\frac{2}{9}}{\frac{2}{9}+\frac{1}{3}}=\frac{2}{5}.\)
Extra questions
- \(\frac{2}{3}.\frac{2}{3}.\frac{2}{3}=\frac{8}{27}\)
- \(1-\frac{8}{27}=\frac{19}{27}\)
- \(\frac{\frac{4}{27}}{\frac{19}{27}}=\frac{4}{19}\)
Question
The local Football Association consists of ten teams. Team \(A\) has a 40 % chance of winning any game against a higher-ranked team, and a 75 % chance of winning any game against a lower-ranked team. If \(A\) is currently in fourth position, find the probability that \(A\) wins its next game.
▶️Answer/Explanation
Ans:
Required probability = \(p(A\) plays a higher ranked team and wins\()\) + \(p(A\) plays a lower ranked team and wins\()\)
=\(\frac{3}{9}×\frac{2}{5}+\frac{6}{9}×\frac{3}{4}=\frac{19}{30}\)
Question
A bag contains 2 red balls, 3 blue balls and 4 green balls. A ball is chosen at random from the bag and is not replaced. A second ball is chosen. Find the probability of choosing one green ball and one blue ball in any order.
▶️Answer/Explanation
Ans:
Using a tree diagram,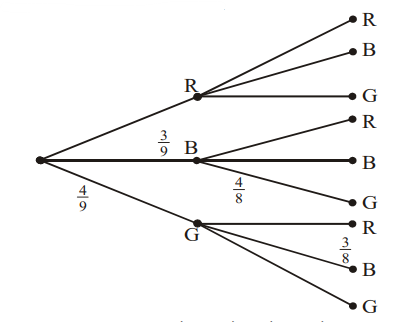
\(p(BG \space or \space GB)=(\frac{3}{9}×\frac{4}{8})+(\frac{4}{9}×\frac{3}{8})=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\)
OR \(p(BG \space or \space GB)=2×\frac{4}{9}×\frac{3}{8}=\frac{1}{3}\)
Question
There are 25 disks in a bag. Some of them are black and the rest are white. Two are simultaneously selected at random. Given that the probability of selecting two disks of the same colour is equal to the probability of selecting two disks of different colour, how many black disks are there in the bag?
▶️Answer/Explanation
Ans:
Let there be \(n\) black disks and \(25-n\) white disks.
EITHER
Since the two probabilities are equal,
\(\frac{1}{2}=\frac{\begin{pmatrix} n\\ 2\end{pmatrix}+\begin{pmatrix} 25-n\\ 2\end{pmatrix}}{\begin{pmatrix} 25\\ 2\end{pmatrix}}\)
\(\frac{1}{2}\begin{pmatrix} 25\\ 2\end{pmatrix}=\frac{n!}{(n-2)!2!}+\frac{(25-n)!}{(23-n)!2!}\)
\(300=n(n-1)+(25-n)(24-n)\)
\(0=2n^2-50n+300\)
\(0=n^2-25n+150\)
\(0=(n-15)(n-10)\)
\(n=15,10\)
OR
\(P(same \space color)=\frac{n(n-1)}{25×24}+\frac{(25-n)(24-n)}{25×24}\)
\(P(different \space color)=\frac{n(25-n)}{25×24}+\frac{(25-n)n}{25×24}\)
probabilities the same so,
\(\frac{n(n-1)}{25×24}+\frac{(25-n)(24-n)}{25×24}\)=\(\frac{n(25-n)}{25×24}+\frac{(25-n)n}{25×24}\)
\(n^2-n+600-49n+n^2=25n-n^2+25n-n^2\)
\(4n^2-100n+600=0\)
\(n^2-25n+150=0\)
\((n-10)(n-15)=0\)
\(n=10,15\)
Question
Bag 1 contains 4 red cubes and 5 blue cubes. Bag 2 contains 7 red cubes and 2 blue cubes. Two cubes are drawn at random, the first from Bag 1 and the second from Bag 2.
- Find the probability that the cubes are of the same colour.
- Given that the cubes selected are of different colours, find the probability that the red cube was selected from Bag 1.
▶️Answer/Explanation
Ans:
- \(P(same \space colour)=P(R \cap R)+P(B \cap B)\)
\(=(\frac{4}{9})(\frac{7}{9})+(\frac{5}{9})(\frac{2}{9})\)
\(=(\frac{28}{81})+(\frac{10}{81})=\frac{38}{81} (=0.469)\) - \(P(first \space red|different)=\frac{P(R \space and \space then \space B)}{P(R \space and \space then \space B)+P(B \space and \space then \space R)}\)
Note: Accept correct tree diagram for selections.
\(=\frac{(\frac{4}{9})(\frac{2}{9})}{(\frac{4}{9})(\frac{2}{9})+(\frac{5}{9})(\frac{7}{9})}
\left ( =\frac{(\frac{4}{9})(\frac{2}{9})}{1-(\frac{38}{81})}=\frac{(\frac{8}{81})}{(\frac{43}{81})} \right ) \)
\(=\frac{8}{43} (=0.186)\)
Question
Jack and Jill play a game, by throwing a die in turn. If the die shows a 1, 2, 3 or 4, the player who threw the die wins the game. If the die shows a 5 or 6, the other player has the next throw. Jack plays first and the game continues until there is a winner.
- Write down the probability that Jack wins on his first throw.
- Calculate the probability that Jill wins on her first throw.
- Calculate the probability that Jack wins the game.
▶️Answer/Explanation
Ans:
- Probability that Jack wins on his first throw \(=\frac{2}{3}(or \space 0.667)\).
- Probability that Jill wins on her first throw:\(\frac{1}{3}×\frac{2}{3}=\frac{2}{9}(or \space 0.222 )\).
- EITHER Probability that Jack wins the game:
\((\frac{2}{3})+(\frac{1}{3}×\frac{1}{3}×\frac{2}{3})+…=\frac{2}{3}×\frac{1}{1-\frac{1}{9}}=\frac{3}{4}\)
OR If \(p\) is the probability that Jack wins the game then
\(p=\frac{2}{3}+\frac{1}{3}×\frac{1}{3}p,\) so that \(p=\frac{3}{4}\)
Question
In a promotion to try to increase the sales of a particular brand of breakfast cereal, a picture of a soccer player is put in each packet. There are ten different pictures available. Each picture is equally likely to be found in any packet of breakfast cereal. Charlotte buys four packets of breakfast cereal.
- Find the probability that the four pictures in these packets are all different.
- Of the ten players whose pictures are in the packets, her favourites are Alan and Bob. Find the probability that she finds at least one picture of a favourite player in these four packets.
▶️Answer/Explanation
Ans:
- \(1×\frac{9}{10}×\frac{8}{10}×\frac{7}{10}=\frac{504}{1000}=0.504\)
- In any packet the probability of not getting pictures of Alan or Bob = \(\frac{8}{10}\)
In four packets the probability of not getting pictures of Alan or Bob is \((\frac{8}{10})^4\)
Required probability is \(1-(\frac{8}{10})^4\)
\(=0.590 (accept \space 0.5904)\)
Question
[modified to include more cases]
An integer is chosen at random from the first one thousand positive integers.
Let \(A\) = {multiples of 4} and \(B\) = {multiples of 6} .
Then \(A \cap B\) = {multiples of 12} (since the least common multiple of 4 and 6 is 12)
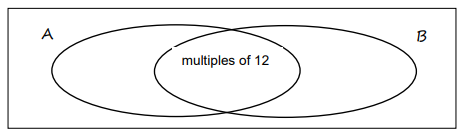
- Find the number of multiples
(i) of 4 (ii) of 6 (iii) of 12 - Find the probability that the integer chosen is a multiple of 4.
- Find the probability that the integer chosen is a multiple of 6.
- Find the probability that the integer chosen is a multiple of both 4 and 6.
- Find the probability that the integer chosen is a multiple of 4 but not of 6.
- Find the probability that the integer chosen is a multiple of 4 or 6.
- Find the probability that the integer chosen is a multiple of 4 or 6 but not both.
▶️Answer/Explanation
Ans:
- (i) 250 (ii) 166 (since 1000/6=166.67) (iii) 83
- 250/1000 = 1/4
- 166/1000
- 83/1000
- 250-83 = 167 so \(P\)=167/1000.
- 250 + 166 – 83 = 333 so \(P\)=333/1000
- 250 + 166 – 2×83 = 250 so \(P\)=250/1000.
Question
At a building site the probability, \(P(A)\), that all materials arrive on time is 0.85. The probability, \(P(B)\), that the building will be completed on time is 0.60. The probability that the materials arrive on time and that the building is completed on time is 0.55.
- Show that events \(A\) and \(B\) are not independent.
- All the materials arrive on time. Find the probability that the building will not be completed on time.
▶️Answer/Explanation
Ans:
- To be independent \(P(A \cap B)=P(A)×P(B)\)
\(P(A)×P(B)=(0.85)(0.60)=0.51\) but \(P(A \cap B)=0.55\)
\(P(A \cap B) \ne P(A)×P(B).\) Hence \(A\) and \(B\) are not independent.
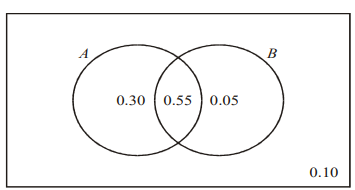
\(P(B’|A)=\frac{P(B’ \cap A)}{P(A)}=\frac{0.30}{0.85}=\frac{6}{17}(=0.353)\)
Question
Bag \(A\) contains 2 red and 3 green balls.
- Two balls are chosen at random from the bag without replacement. Find the probability that 2 red balls are chosen.
Bag \(B\) contains 4 red and \(n\) green balls. - Two balls are chosen without replacement from this bag. If the probability that two red balls are chosen is \(\frac{2}{15}\), show that \(n = 6.\)
A standard die with six faces is rolled. If a 1 or 6 is obtained, two balls are chosen from bag \(A\), otherwise two balls are chosen from bag \(B\) - Calculate the probability that two red balls are chosen.
- Given that two red balls are chosen, find the probability that a 1 or a 6 was obtained on the die.
▶️Answer/Explanation
Ans:
- \(P(RR)=(\frac{2}{5})(\frac{1}{4})=\frac{1}{10}\)
- \(P(RR)=\frac{4}{4+n}×\frac{3}{3+n}=\frac{2}{15}\)
Forming equation \(12×5=2(4+n)(3+n)\)
\(12+7n+n^2=90\)⇒\(n^2+7n-78=0\)⇒\(n=6\) - EITHER
\(P(A)=\frac{1}{3}\) \(P(B)=\frac{2}{3}\)
\(P(RR)=P(A \cap RR)+P(B \cap RR)=(\frac{1}{3})(\frac{1}{10})+(\frac{2}{3})(\frac{2}{15})=\frac{11}{90}\)
OR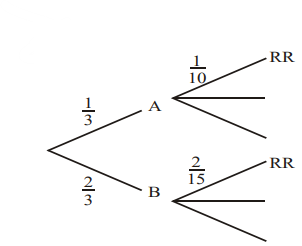
\(P(RR)=\frac{1}{3}×\frac{1}{10}+\frac{2}{3}×\frac{2}{15}=\frac{11}{90}\)
d. \(P(1 \space or \space 6) = P(A)\)
\(P(A|RR)=\frac{P(A \cap RR)}{P(RR)}\)
\(=\frac{\left [ (\frac{1}{3})(\frac{1}{10}) \right ]}{\frac{11}{90}}=\frac{3}{11}\)
Question
Two women, Ann and Bridget, play a game in which they take it in turns to throw an unbiased six-sided die. The first woman to throw a ‘6’ wins the game. Ann is the first to throw.
- Find the probability that
- Bridget wins on her first throw;
- Ann wins on her second throw;
- Ann wins on her \(n^{th}\) throw.
- Let \(p\) be the probability that Ann wins the game. Show that \(p=\frac{1}{6}+\frac{25}{36}p\).
- Find the probability that Bridget wins the game.
- Suppose that the game is played six times. Find the probability that Ann wins more games than Bridget.
▶️Answer/Explanation
Ans:
- \(P\)(Bridget wins on her first throw) = \(\frac{5}{6}×\frac{1}{6}=\frac{5}{36}\)
- \(P\)(Ann wins on her second throw) = \(\frac{5}{6}×\frac{1}{6}×\frac{1}{6}=\frac{25}{216}\)
- \(P\)(Ann wins on her \(n^{th}\) throw) = \((\frac{5}{6})^{2(n-1)}×\frac{1}{6}\).
- \(p = P\)(Ann wins)
= \(P\)(Ann wins on her first throw) + \(P\)(both Ann and Bridget do not win on their first throws) × \(P\)(Ann wins from then on)
=\(\frac{1}{6}+(\frac{5}{6})^2×p=\frac{1}{6}+\frac{25}{36}p\)
OR
\(p\) = \(P\)(Ann wins on first throw) + \(P\)(Ann wins on second throw) + \(P\)(Ann wins on third throw) + ….
=\(\frac{1}{6}+(\frac{5}{6})^2\frac{1}{6}+(\frac{5}{6})^4\frac{1}{6}+\)….
=\(\frac{1}{6}+\frac{25}{36}\left \{ \frac{1}{6}+(\frac{5}{6})^2(\frac{1}{6})+(\frac{5}{6})^4(\frac{1}{6})+… \right \}\)( or \(\frac{\frac{1}{6}}{1-\frac{25}{36}}\))
=\(\frac{1}{6}+\frac{25}{36}p,\) as required. - From part (b), \(\frac{11}{36}p=\frac{1}{6}\)⇒\(p=\frac{6}{11}\).
Therefore, \(P\)(Bridget wins)=\(1-p=\frac{5}{11}\) - \(P\)(Ann wins more games than Bridget)= \(P\)(Ann wins 4 games) + \(P\)(Ann wins 5 games) + \(P\)(Ann wins 6 games)
=\((\frac{6}{4})(\frac{6}{11})^4(\frac{5}{11})^2+(\frac{6}{5})(\frac{6}{11})^5(\frac{5}{11})+(\frac{6}{11})^6\)
=\(\frac{6^4}{11^6}(15×25+36×5+36)=0.432\)
Question
- Find the probability that a number, chosen at random between 200 and 800 inclusive, will be a multiple of 9.
- Find the sum of the numbers between 200 and 800 inclusive, which are multiples of 6, but not multiples of 9.
▶️Answer/Explanation
Ans:
- The number of multiples of 9 is 66.
There are 601 numbers between 200 and 800
Probability =\(\frac{66}{601}(=0.110)\) - The number of multiples of 6 is 100
\(S_{100}=\frac{100}{2}(204+798)=50100\)
Multiples of 6 and 9 are multiples of 18
The number of multiples of 18 is 33
\(S_{33}=16632\)
The sum of numbers which are multiples of 6 but not of 9 is