Question
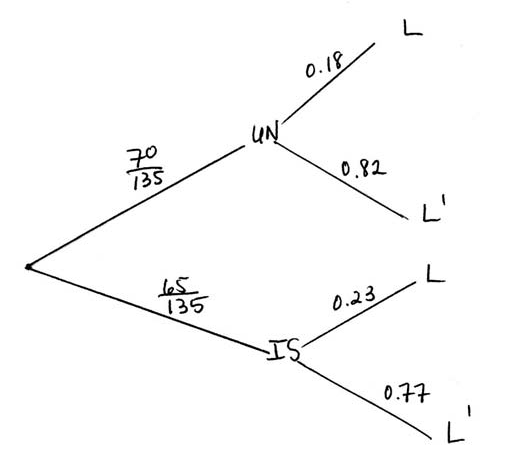
Only two international airlines fly daily into an airport. UN Air has 70 flights a day and IS Air has 65 flights a day. Passengers flying with UN Air have an 18 % probability of losing their luggage and passengers flying with IS Air have a 23 % probability of losing their luggage. You overhear someone in the airport complain about her luggage being lost.
Find the probability that she travelled with IS Air.
▶️Answer/Explanation
Markscheme
METHOD 1
(M1)
Let P(I) be the probability of flying IS Air, P(U) be the probability flying UN Air and P(L) be the probability of luggage lost.
\({\text{P}}(I|L) = \frac{{{\text{P}}(I \cap L)}}{{{\text{P}}(L)}}{\text{ }}\left( {{\text{or Bayes’ formula , P}}(I|L) = \frac{{{\text{P}}(L|I){\text{P}}(I)}}{{{\text{P}}(L|I){\text{P}}(I) + {\text{P}}(L|U){\text{P}}(U)}}} \right)\) (M1)
\( = \frac{{0.23 \times \frac{{65}}{{135}}}}{{0.18 \times \frac{{70}}{{135}} + 0.23 \times \frac{{65}}{{135}}}}\) A1A1A1
\( = \frac{{299}}{{551}}{\text{ }}( = 0.543,{\text{ accept }}0.542)\) A1
[6 marks]
METHOD 2
Expected number of suitcases lost by UN Air is \(0.18 \times 70 = 12.6\) M1A1
Expected number of suitcases lost by IS Air is \(0.23 \times 65 = 14.95\) A1
\({\text{P}}(I|L) = \frac{{14.95}}{{12.6 + 14.95}}\) M1A1
\( = 0.543\) A1
[6 marks]
Examiners report
This question was well answered by the majority of candidates. Most candidates used either tree diagrams or expected value methods.
Question
(a) Find the percentage of the population that has been vaccinated.
(b) A randomly chosen person catches the virus. Find the probability that this person has been vaccinated.
▶️Answer/Explanation
Markscheme
(a)
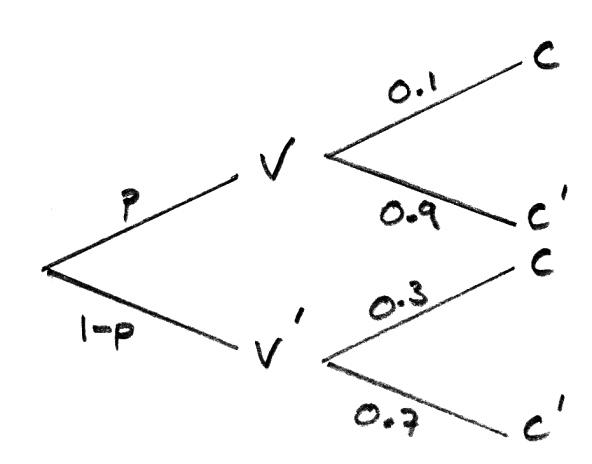
using the law of total probabilities: (M1)
\(0.1p + 0.3\left( {1 – p} \right) = 0.22\) A1
\(0.1p + 0.3 – 0.3p = 0.22\)
\(0.2p = 0.88\)
\(p = \frac{{0.88}}{{0.2}} = 0.4\)
\(p = 40\% \) (accept \(0.4\)) A1
(b) required probability \( = \frac{{0.4 \times 0.1}}{{0.22}}\) M1
\( = \frac{2}{{11}}\) (\(0.182\)) A1
[5 marks]
Examiners report
Most candidates who successfully answered this question had first drawn a tree diagram, using a symbol to denote the probability that a randomly chosen person had received the influenza virus. For those who did not draw a tree diagram, there was poor understanding of how to apply the conditional probability formula.
Question
Josie has three ways of getting to school. \(30\% \) of the time she travels by car, \(20\% \) of the time she rides her bicycle and \(50\% \) of the time she walks.
When travelling by car, Josie is late \(5\% \) of the time. When riding her bicycle she is late \(10\% \) of the time. When walking she is late \(25\% \) of the time. Given that she was on time, find the probability that she rides her bicycle.
▶️/Explanation
Markscheme
EITHER
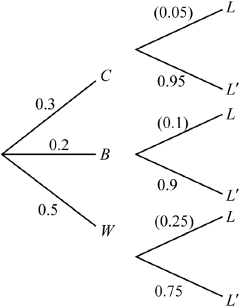M1A1A1
Note: Award M1 for a two-level tree diagram, A1 for correct first level probabilities, and A1 for correct second level probabilities.
OR
\({\text{P}}(B|L’) = \frac{{{\text{P}}(L’|B){\text{P}}(B)}}{{{\text{P}}(L’|B){\text{P}}(B) + {\text{P}}(L’|C){\text{P}}(C) + {\text{P}}(L’|W){\text{P}}(Q)}}\;\;\;\left( { = \frac{{{\text{P}}(B \cap L’}}{{{\text{P}}(L’)}}} \right)\) (M1)(A1)(A1)
THEN
\({\text{P}}(B|L’) = \frac{{0.9 \times 0.2}}{{0.9 \times 0.2 + 0.95 \times 0.3 + 0.75 \times 0.5}}\;\;\;\left( { = \frac{{0.18}}{{0.84}}} \right)\) M1A1
\( = 0.214\;\;\;\left( { = \frac{3}{{14}}} \right)\) A1
[6 marks]