Question
A biased coin is tossed five times. The probability of obtaining a head in any one throw is \(p\).
Let \(X\) be the number of heads obtained.
Find, in terms of \(p\), an expression for \({\text{P}}(X = 4)\).
(i) Determine the value of \(p\) for which \({\text{P}}(X = 4)\) is a maximum.
(ii) For this value of \(p\), determine the expected number of heads.
▶️Answer/Explanation
Markscheme
\(X \sim {\text{B}}(5,{\text{ }}p)\) (M1)
\({\text{P}}(X = 4) = \left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right){p^4}(1 – p)\) (or equivalent) A1
[2 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}p}}(5{p^4} – 5{p^5}) = 20{p^3} – 25{p^4}\) M1A1
\(5{p^3}(4 – 5p) = 0 \Rightarrow p = \frac{4}{5}\) M1A1
Note: Do not award the final A1 if \(p = 0\) is included in the answer.
(ii) \({\text{E}}(X) = np = 5\left( {\frac{4}{5}} \right)\) (M1)
\( = 4\) A1
[6 marks]
Examiners report
This question was generally very well done and posed few problems except for the weakest candidates.
This question was generally very well done and posed few problems except for the weakest candidates.
Question
A biased coin is tossed five times. The probability of obtaining a head in any one throw is \(p\).
Let \(X\) be the number of heads obtained.
Find, in terms of \(p\), an expression for \({\text{P}}(X = 4)\).
(i) Determine the value of \(p\) for which \({\text{P}}(X = 4)\) is a maximum.
(ii) For this value of \(p\), determine the expected number of heads.
▶️Answer/Explanation
Markscheme
\(X \sim {\text{B}}(5,{\text{ }}p)\) (M1)
\({\text{P}}(X = 4) = \left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right){p^4}(1 – p)\) (or equivalent) A1
[2 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}p}}(5{p^4} – 5{p^5}) = 20{p^3} – 25{p^4}\) M1A1
\(5{p^3}(4 – 5p) = 0 \Rightarrow p = \frac{4}{5}\) M1A1
Note: Do not award the final A1 if \(p = 0\) is included in the answer.
(ii) \({\text{E}}(X) = np = 5\left( {\frac{4}{5}} \right)\) (M1)
\( = 4\) A1
[6 marks]
Examiners report
This question was generally very well done and posed few problems except for the weakest candidates.
This question was generally very well done and posed few problems except for the weakest candidates.
Question
Chloe and Selena play a game where each have four cards showing capital letters A, B, C and D.
Chloe lays her cards face up on the table in order A, B, C, D as shown in the following diagram.
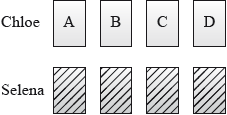
Selena shuffles her cards and lays them face down on the table. She then turns them over one by one to see if her card matches with Chloe’s card directly above.
Chloe wins if no matches occur; otherwise Selena wins.
Chloe and Selena repeat their game so that they play a total of 50 times.
Suppose the discrete random variable X represents the number of times Chloe wins.
Show that the probability that Chloe wins the game is \(\frac{3}{8}\).
Determine the mean of X.
Determine the variance of X.
▶️Answer/Explanation
Markscheme
METHOD 1
number of possible “deals” \( = 4! = 24\) A1
consider ways of achieving “no matches” (Chloe winning):
Selena could deal B, C, D (ie, 3 possibilities)
as her first card R1
for each of these matches, there are only 3 possible combinations for the remaining 3 cards R1
so no. ways achieving no matches \( = 3 \times 3 = 9\) M1A1
so probability Chloe wins \( = \frac{9}{{23}} = \frac{3}{8}\) A1AG
METHOD 2
number of possible “deals” \( = 4! = 24\) A1
consider ways of achieving a match (Selena winning)
Selena card A can match with Chloe card A, giving 6 possibilities for this happening R1
if Selena deals B as her first card, there are only 3 possible combinations for the remaining 3 cards. Similarly for dealing C and dealing D R1
so no. ways achieving one match is \( = 6 + 3 + 3 + 3 = 15\) M1A1
so probability Chloe wins \( = 1 – \frac{{15}}{{24}} = \frac{3}{8}\) A1AG
METHOD 3
systematic attempt to find number of outcomes where Chloe wins (no matches)
(using tree diag. or otherwise) M1
9 found A1
each has probability \(\frac{1}{4} \times \frac{1}{3} \times \frac{1}{2} \times 1\) M1
\( = \frac{1}{{24}}\) A1
their 9 multiplied by their \(\frac{1}{{24}}\) M1A1
\( = \frac{3}{8}\) AG
[6 marks]
\(X \sim {\text{B}}\left( {50,{\text{ }}\frac{3}{8}} \right)\) (M1)
\(\mu = np = 50 \times \frac{3}{8} = \frac{{150}}{8}{\text{ }}\left( { = \frac{{75}}{4}} \right){\text{ }}( = 18.75)\) (M1)A1
[3 marks]
\({\sigma ^2} = np(1 – p) = 50 \times \frac{3}{8} \times \frac{5}{8} = \frac{{750}}{{64}}{\text{ }}\left( { = \frac{{375}}{{32}}} \right){\text{ }}( = 11.7)\) (M1)A1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Chloe and Selena play a game where each have four cards showing capital letters A, B, C and D.
Chloe lays her cards face up on the table in order A, B, C, D as shown in the following diagram.

Selena shuffles her cards and lays them face down on the table. She then turns them over one by one to see if her card matches with Chloe’s card directly above.
Chloe wins if no matches occur; otherwise Selena wins.
Chloe and Selena repeat their game so that they play a total of 50 times.
Suppose the discrete random variable X represents the number of times Chloe wins.
Show that the probability that Chloe wins the game is \(\frac{3}{8}\).
Determine the mean of X.
Determine the variance of X.
▶️Answer/Explanation
Markscheme
METHOD 1
number of possible “deals” \( = 4! = 24\) A1
consider ways of achieving “no matches” (Chloe winning):
Selena could deal B, C, D (ie, 3 possibilities)
as her first card R1
for each of these matches, there are only 3 possible combinations for the remaining 3 cards R1
so no. ways achieving no matches \( = 3 \times 3 = 9\) M1A1
so probability Chloe wins \( = \frac{9}{{23}} = \frac{3}{8}\) A1AG
METHOD 2
number of possible “deals” \( = 4! = 24\) A1
consider ways of achieving a match (Selena winning)
Selena card A can match with Chloe card A, giving 6 possibilities for this happening R1
if Selena deals B as her first card, there are only 3 possible combinations for the remaining 3 cards. Similarly for dealing C and dealing D R1
so no. ways achieving one match is \( = 6 + 3 + 3 + 3 = 15\) M1A1
so probability Chloe wins \( = 1 – \frac{{15}}{{24}} = \frac{3}{8}\) A1AG
METHOD 3
systematic attempt to find number of outcomes where Chloe wins (no matches)
(using tree diag. or otherwise) M1
9 found A1
each has probability \(\frac{1}{4} \times \frac{1}{3} \times \frac{1}{2} \times 1\) M1
\( = \frac{1}{{24}}\) A1
their 9 multiplied by their \(\frac{1}{{24}}\) M1A1
\( = \frac{3}{8}\) AG
[6 marks]
\(X \sim {\text{B}}\left( {50,{\text{ }}\frac{3}{8}} \right)\) (M1)
\(\mu = np = 50 \times \frac{3}{8} = \frac{{150}}{8}{\text{ }}\left( { = \frac{{75}}{4}} \right){\text{ }}( = 18.75)\) (M1)A1
[3 marks]
\({\sigma ^2} = np(1 – p) = 50 \times \frac{3}{8} \times \frac{5}{8} = \frac{{750}}{{64}}{\text{ }}\left( { = \frac{{375}}{{32}}} \right){\text{ }}( = 11.7)\) (M1)A1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
A discrete random variable X has a probability distribution given in the following table.

(a) \({\text{E}}(X) = 2.61\), determine the value of p and of q.
(b) Calculate \({\text{Var}}(X)\) to three significant figures.
▶️Answer/Explanation
Markscheme
(a) \(p + q = 0.44\) A1
\(2.5p + 3.5q = 1.25\) (M1)A1
\(p = 0.29,{\text{ }}q = 0.15\) A1
(b) use of \({\text{Var}}(X) = {\text{E}}({X^2}) – {\text{E}}{(X)^2}\) (M1)
\({\text{Var}}(X) = 2.10\) A1
[6 marks]
Examiners report
An easy question, well answered by most candidates. For the others it was disappointing that many did not use the fact that the probabilities add to unity.
Question
Tim throws two identical fair dice simultaneously. Each die has six faces: two faces numbered 1, two faces numbered 2 and two faces numbered 3. His score is the sum of the two numbers shown on the dice.
(a) (i) Calculate the probability that Tim obtains a score of 6.
(ii) Calculate the probability that Tim obtains a score of at least 3.
Tim plays a game with his friend Bill, who also has two dice numbered in the same way. Bill’s score is the sum of the two numbers shown on his dice.
(b) (i) Calculate the probability that Tim and Bill both obtain a score of 6.
(ii) Calculate the probability that Tim and Bill obtain the same score.
(c) Let X denote the largest number shown on the four dice.
(i) Show that \({\text{P}}(X \leqslant 2) = \frac{{16}}{{81}}\).
(ii) Copy and complete the following probability distribution table.
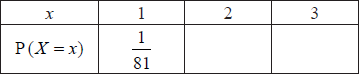
(iii) Calculate \({\text{E}}(X)\) and \({\text{E}}({X^2})\) and hence find \({\text{Var}}(X)\).
(d) Given that X = 3, find the probability that the sum of the numbers shown on the four dice is 8.
▶️Answer/Explanation
Markscheme
(a) let T be Tim’s score
(i) \({\text{P}}(T = 6) = \frac{{11}}{9}{\text{ }}( = 0.111{\text{ 3 sf)}}\) A1
(ii) \({\text{P}}(T \geqslant 3) = 1 – {\text{P}}(T \leqslant 2) = 1 – \frac{1}{9} = \frac{8}{9}{\text{ }}( = 0.889{\text{ 3 sf)}}\) (M1)A1
[3 marks]
(b) let B be Bill’s score
(i) \({\text{P}}(T = 6{\text{ and }}B = 6) = \frac{1}{9} \times \frac{1}{9} = \frac{1}{{81}}{\text{ }}( = 0.012{\text{ 3 sf)}}\) (M1)A1
(ii) \({\text{P}}(B = T) = {\text{P}}(2){\text{P}}(2) + {\text{P}}(3){\text{P}}(3) + \ldots + {\text{P}}(6){\text{P}}(6)\)
\( = \frac{1}{9} \times \frac{1}{9} + \frac{2}{9} \times \frac{2}{9} + \frac{3}{9} \times \frac{3}{9} + \frac{2}{9} \times \frac{2}{9} + \frac{1}{9} \times \frac{1}{9}\) M1
\( = \frac{{19}}{{81}}{\text{ }}( = 0.235{\text{ 3 sf)}}\) A1
[4 marks]
(c) (i) EITHER
\({\text{P}}(X \leqslant 2) = \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}\) M1A1
because \({\text{P}}(X \leqslant 2) = {\text{P}}\left( {(a,{\text{ }}b,{\text{ }}c,{\text{ }}d)|a,{\text{ }}b,{\text{ }}c,{\text{ }}d = 1,{\text{ }}2} \right)\) R1
or equivalent
\({\text{P}}(X \leqslant 2) = \frac{{16}}{{81}}\) AG
OR
there are sixteen possible permutations which are
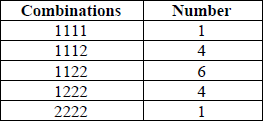 M1A1
M1A1
Note: This information may be presented in a variety of forms.
\({\text{P}}(X \leqslant 2) = \frac{{1 + 4 + 6 + 4 + 1}}{{81}}\) A1
\( = \frac{{16}}{{81}}\) AG
(ii) 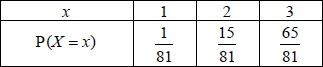 A1A1
A1A1
(iii) \({\text{E}}(X) = \sum\limits_{x = 1}^3 {x{\text{P}}(X = x)} \) (M1)
\( = \frac{1}{{81}} + \frac{{30}}{{81}} + \frac{{195}}{{81}}\)
\( = \frac{{226}}{{81}}\,\,\,\,\,\)(2.79 to 3 sf) A1
\({\text{E}}({X^2}) = \sum\limits_{x = 1}^3 {{x^2}{\text{P}}(X = x)} \)
\( = \frac{1}{{81}} + \frac{{60}}{{81}} + \frac{{585}}{{81}}\)
\( = \frac{{646}}{{81}}\,\,\,\,\,\)(7.98 to 3 sf) A1
\({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2}\) (M1)
\( = 0.191\) (3 sf) A1
Note: Award M1A0 for answers obtained using rounded values \(\left( {e.g.{\text{ Var}}(X) = 0.196} \right)\).
[10 marks]
(d)
\({\text{P}}\left( {{\text{total is }}8 \cap (X = 3)} \right) = \frac{{18}}{{81}}\) M1A1
since \({\text{P}}(X = 3) = \frac{{65}}{{81}}\)
\({\text{P}}\left( {{\text{total is }}8|(X = 3)} \right) = \frac{{{\text{P}}\left( {({\text{total is 8)}} \cap (X = 3)} \right)}}{{{\text{P}}(X = 3)}}\) M1
\( = \frac{{18}}{{65}}{\text{ }}( = 0.277)\) A1
[4 marks]
Total [21 marks]
Examiners report
Most candidates with a reasonable understanding of probability managed to answer well parts (a), (b) and some of part (c). However some candidates did not realize that different scores were not equally likely which lead to incorrect answers in several parts. Surprisingly, many candidates completed the table in part c) ii) with values that did not add up to 1. Very few candidates answered part (d) well. The enumeration of possible cases was sometimes attempted but with little success.
Question
The probability density function of the continuous random variable X is given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k{2^{\frac{1}{x}}},}&{1 \leqslant x \leqslant 2} \\
{0,}&{{\text{otherwise}}}
\end{array}} \right.\]
where k is a constant. Find the expected value of X .
▶️Answer/Explanation
Markscheme
\(k\int_1^2 {{2^{\frac{1}{x}}}{\text{d}}x = 1 \Rightarrow k = \frac{1}{{\int_1^2 {{2^{\frac{1}{x}}}{\text{d}}x} }}{\text{ }}( = 0.61556…)} \) (M1)(A1)
\({\text{E}}(X) = k\int_1^2 {x{2^{\frac{1}{x}}}{\text{d}}x = 2.39….k{\text{ or 1.47}}} \) M1A1
Note: Condone missing dx in any part of the question.
[4 marks]
Examiners report
This question was well attempted by most candidates. However many were not alert for the necessity of using GDC to calculate the definite integrals and wasted time trying to obtain these values using standard calculus methods without success.
Question
The probability density function of a continuous random variable X is given by
\(f(x) = \frac{1}{{1 + {x^4}}}\), \(0\) \(”\) \(x\) \(”\) \(a\) .
Find the value of a .
Find the mean of X .
▶️Answer/Explanation
Markscheme
\(\int_0^a {\frac{1}{{1 + {x^4}}}{\text{d}}x = 1} \) M2
a = 1.40 A1
[3 marks]
\({\text{E}}(X) = \int_0^a {\frac{x}{{1 + {x^4}}}{\text{d}}x} \) M1
\(\left( { = \frac{1}{2}\arctan ({a^2})} \right)\)
= 0.548 A1
[2 marks]
Examiners report
Many candidates picked up some marks for this question, but only a few gained full marks. In part (a) many candidates did not appreciate the need for the calculator to find a value of a. Candidates had more success with part (b) with a number of candidates picking up follow through marks.
Many candidates picked up some marks for this question, but only a few gained full marks. In part (a) many candidates did not appreciate the need for the calculator to find a value of a. Candidates had more success with part (b) with a number of candidates picking up follow through marks.
Question
The length, X metres, of a species of fish has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{r}}
{a{x^2},}&{{\text{for }}0 \leqslant x \leqslant 0.5} \\
{0.5a(1 – x),}&{{\text{for }}0.5 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise }}{\text{.}}}
\end{array}} \right.\]
Show that a = 9.6.
Sketch the graph of the distribution.
Find \({\text{P}}(X < 0.6)\).
▶️Answer/Explanation
Markscheme
\(\int_0^{0.5} {a{x^2}{\text{d}}x + \int_{0.5}^1 {0.5a(1 – x){\text{d}}x = 1} } \) M1A1
\(\frac{{5a}}{{48}}\) (or equivalent) or \(a \times 0.104 \ldots = 1\) A1
Note: Award M1 for considering two definite integrals.
Award A1 for equating to 1.
Award A1 for a correct equation.
The A1A1 can be awarded in any order.
a = 9.6 AG
[3 marks]
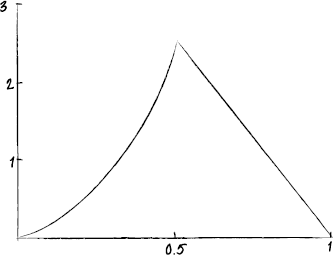
correct shape for \(0 \leqslant x \leqslant 0.5\) and \(f(0.5) \approx 2.4\) A1
correct shape for \(0.5 \leqslant x \leqslant 1\) and \(f(1) = 0\) A1
[2 marks]
attempting to find \({\text{P}}(X < 0.6)\) (M1)
direct GDC use or eg \({\text{P}}(0 \leqslant X \leqslant 0.5) + {\text{P}}(0.5 \leqslant X \leqslant 0.6)\) or \(1 – {\text{P}}(0.6 \leqslant X \leqslant 1)\)
\({\text{P}}(X < 0.6) = 0.616{\text{ }}\left( { = \frac{{77}}{{125}}} \right)\) A1
[2 marks]
Examiners report
Part (a) was generally well done. Common errors usually involved not recognizing that the sum of the two integrals was equal to one, premature rounding or not showing full working to conclusively show that a = 9.6.
Part (b) was not well done with many graphs poorly labelled and offering no reference to domain and range.
Part (c) was reasonably well done. The most common error involved calculating an incorrect probability from an incorrect definite integral.
Question
The length, X metres, of a species of fish has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{r}}
{a{x^2},}&{{\text{for }}0 \leqslant x \leqslant 0.5} \\
{0.5a(1 – x),}&{{\text{for }}0.5 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise }}{\text{.}}}
\end{array}} \right.\]
Show that a = 9.6.
Sketch the graph of the distribution.
Find \({\text{P}}(X < 0.6)\).
▶️Answer/Explanation
Markscheme
\(\int_0^{0.5} {a{x^2}{\text{d}}x + \int_{0.5}^1 {0.5a(1 – x){\text{d}}x = 1} } \) M1A1
\(\frac{{5a}}{{48}}\) (or equivalent) or \(a \times 0.104 \ldots = 1\) A1
Note: Award M1 for considering two definite integrals.
Award A1 for equating to 1.
Award A1 for a correct equation.
The A1A1 can be awarded in any order.
a = 9.6 AG
[3 marks]
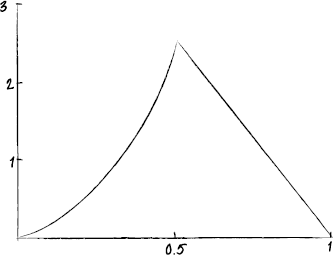
correct shape for \(0 \leqslant x \leqslant 0.5\) and \(f(0.5) \approx 2.4\) A1
correct shape for \(0.5 \leqslant x \leqslant 1\) and \(f(1) = 0\) A1
[2 marks]
attempting to find \({\text{P}}(X < 0.6)\) (M1)
direct GDC use or eg \({\text{P}}(0 \leqslant X \leqslant 0.5) + {\text{P}}(0.5 \leqslant X \leqslant 0.6)\) or \(1 – {\text{P}}(0.6 \leqslant X \leqslant 1)\)
\({\text{P}}(X < 0.6) = 0.616{\text{ }}\left( { = \frac{{77}}{{125}}} \right)\) A1
[2 marks]
Examiners report
Part (a) was generally well done. Common errors usually involved not recognizing that the sum of the two integrals was equal to one, premature rounding or not showing full working to conclusively show that a = 9.6.
Part (b) was not well done with many graphs poorly labelled and offering no reference to domain and range.
Part (c) was reasonably well done. The most common error involved calculating an incorrect probability from an incorrect definite integral.
Question
The length, X metres, of a species of fish has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{r}}
{a{x^2},}&{{\text{for }}0 \leqslant x \leqslant 0.5} \\
{0.5a(1 – x),}&{{\text{for }}0.5 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise }}{\text{.}}}
\end{array}} \right.\]
Show that a = 9.6.
Sketch the graph of the distribution.
Find \({\text{P}}(X < 0.6)\).
▶️Answer/Explanation
Markscheme
\(\int_0^{0.5} {a{x^2}{\text{d}}x + \int_{0.5}^1 {0.5a(1 – x){\text{d}}x = 1} } \) M1A1
\(\frac{{5a}}{{48}}\) (or equivalent) or \(a \times 0.104 \ldots = 1\) A1
Note: Award M1 for considering two definite integrals.
Award A1 for equating to 1.
Award A1 for a correct equation.
The A1A1 can be awarded in any order.
a = 9.6 AG
[3 marks]
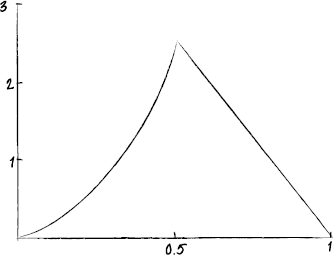
correct shape for \(0 \leqslant x \leqslant 0.5\) and \(f(0.5) \approx 2.4\) A1
correct shape for \(0.5 \leqslant x \leqslant 1\) and \(f(1) = 0\) A1
[2 marks]
attempting to find \({\text{P}}(X < 0.6)\) (M1)
direct GDC use or eg \({\text{P}}(0 \leqslant X \leqslant 0.5) + {\text{P}}(0.5 \leqslant X \leqslant 0.6)\) or \(1 – {\text{P}}(0.6 \leqslant X \leqslant 1)\)
\({\text{P}}(X < 0.6) = 0.616{\text{ }}\left( { = \frac{{77}}{{125}}} \right)\) A1
[2 marks]
Examiners report
Part (a) was generally well done. Common errors usually involved not recognizing that the sum of the two integrals was equal to one, premature rounding or not showing full working to conclusively show that a = 9.6.
Part (b) was not well done with many graphs poorly labelled and offering no reference to domain and range.
Part (c) was reasonably well done. The most common error involved calculating an incorrect probability from an incorrect definite integral.
Question
A small car hire company has two cars. Each car can be hired for one whole day at a time. The rental charge is US$60 per car per day. The number of requests to hire a car for one whole day may be modelled by a Poisson distribution with mean 1.2.
Find the probability that on a particular weekend, three requests are received on Saturday and none are received on Sunday.
Over a weekend of two days, it is given that a total of three requests are received.
Find the expected total rental income for the weekend.
▶️Answer/Explanation
Markscheme
\(X \sim {\text{Po}}(1.2)\)
\({\text{P}}(X = 3) \times {\text{P}}(X = 0)\) (M1)
\( = 0.0867 \ldots \times 0.3011 \ldots \)
\( = 0.0261\) A1
[2 marks]
Three requests over two days can occur as (3, 0), (0, 3), (2, 1) or (1, 2). R1
using conditional probability, for example
\(\frac{{{\text{P}}(3,{\text{ }}0)}}{{{\text{P}}(3{\text{ requests, }}m = 2.4)}} = 0.125{\text{ or }}\frac{{{\text{P}}(2,{\text{ }}1)}}{{{\text{P}}(3{\text{ requests, }}m = 2.4)}} = 0.375\) M1A1
expected income is
\(2 \times 0.125 \times {\text{US}}\$ 120 + 2 \times 0.375 \times {\text{US}}\$ 180\) M1
Note: Award M1 for attempting to find the expected income including both (3, 0) and (2, 1) cases.
\( = {\text{US}}\$ 30 + {\text{US}}\$ 135\)
\( = {\text{US}}\$ 165\) A1
[5 marks]
Examiners report
Part (a) was generally well done although a number of candidates added the two probabilities rather than multiplying the two probabilities. A number of candidates specified the required probability correct to two significant figures only.
Part (b) challenged most candidates with only a few candidates able to correctly employ a conditional probability argument.
Question
The number of cats visiting Helena’s garden each week follows a Poisson distribution with mean \(\lambda = 0.6\).
Find the probability that
(i) in a particular week no cats will visit Helena’s garden;
(ii) in a particular week at least three cats will visit Helena’s garden;
(iii) over a four-week period no more than five cats in total will visit Helena’s garden;
(iv) over a twelve-week period there will be exactly four weeks in which at least one cat will visit Helena’s garden.
A continuous random variable \(X\) has probability distribution function \(f\) given by
\(f(x) = k\ln x\) \(1 \leqslant x \leqslant 3\)
\(f(x) = 0\) otherwise
(i) Find the value of \(k\) to six decimal places.
(ii) Find the value of \({\text{E}}(X)\).
(iii) State the mode of \(X\).
(iv) Find the median of \(X\).
▶️Answer/Explanation
Markscheme
(i) \(X \sim {\text{Po(0.6)}}\)
\({\text{P}}(X = 0) = 0.549{\text{ }}\left( { = {{\text{e}}^{ – 0.6}}} \right)\) A1
(ii) \({\text{P}}(X \geqslant 3) = 1 – {\text{P}}(X \leqslant 2)\) (M1)(A1)
\( = 1 – \left( {{{\text{e}}^{ – 0.6}} + {{\text{e}}^{ – 0.6}} \times 0.6 + {{\text{e}}^{ – 0.6}} \times \frac{{{{0.6}^2}}}{2}} \right)\)
\( = 0.0231\) A1
(iii) \(Y \sim {\text{Po(2.4)}}\) (M1)
\({\text{P}}(Y \leqslant 5) = 0.964\) A1
(iv) \(Z \sim {\text{B(12, 0.451}} \ldots )\) (M1)(A1)
Note: Award M1 for recognising binomial and A1 for using correct parameters.
\({\text{P}}(Z = 4) = 0.169\) A1
[9 marks]
(i) \(k\int_1^3 {\ln x{\text{d}}x = 1} \) (M1)
\((k \times 1.2958 \ldots = 1)\)
\(k = 0.771702\) A1
(ii) \({\text{E}}(X) = \int_1^3 {kx\ln x{\text{d}}x} \) (A1)
attempting to evaluate their integral (M1)
\( = 2.27\) A1
(iii) \(x = 3\) A1
(iv) \(\int_1^m {k\ln x{\text{d}}x = 0.5} \) (M1)
\(k[x\ln x – x]_1^m = 0.5\)
attempting to solve for m (M1)
\(m = 2.34\) A1
[9 marks]
Examiners report
Parts (a) and (b) were generally well done by a large proportion of candidates. In part (a) (ii), some candidates used an incorrect inequality (e.g. \({\text{P}}(X \geqslant 3) = 1 – {\text{P}}(X \leqslant 3)\)) while in (a) (iii) some candidates did not use \(\mu = 2.4\). In part (a) (iv), a number of candidates either did not realise that they needed to consider a binomial random variable or did so using incorrect parameters.
Parts (a) and (b) were generally well done by a large proportion of candidates.
In (b) (i), some candidates gave their value of k correct to three significant figures rather than correct to six decimal places. In parts (b) (i), (ii) and (iv), a large number of candidates unnecessarily used integration by parts. In part (b) (iii), a number of candidates thought the mode of X was \(f(3)\) rather than \(x = 3\). In part (b) (iv), a number of candidates did not consider the domain of f when attempting to find the median or checking their solution.
Question
The continuous random variable \(X\) has the probability distribution function \(f(x) = A\sin \left( {\ln (x)} \right),{\text{ }}1 \le x \le 5\).
Find the value of \(A\) to three decimal places.
Find the mode of \(X\).
Find the value \({\text{P}}(X \le 3|X \ge 2)\).
▶️Answer/Explanation
Markscheme
\(A\int_1^5 {\sin (\ln x){\text{d}}x = 1} \) (M1)
\(A = 0.323{\text{ (3 dp only)}}\) A1
[2 marks]
either a graphical approach or \(f'(x) = \frac{{\cos (\ln x)}}{x} = 0\) (M1)
\(x = 4.81\;\;\;\left( { = {{\text{e}}^{\frac{\pi }{2}}}} \right)\) A1
Note: Do not award A1FT for a candidate working in degrees.
[2 marks]
\({\text{P}}(X \le 3|X \ge 2) = \frac{{{\text{P}}(2 \le X \le 3)}}{{{\text{P}}(X \ge 2)}}\;\;\;\left( { = \frac{{\int_2^3 {\sin \left( {\ln (x)} \right){\text{d}}x} }}{{\int_2^5 {\sin \left( {\ln (x)} \right){\text{d}}x} }}} \right)\) (M1)
\( = 0.288\) A1
Note: Do not award A1FT for a candidate working in degrees.
[2 marks]
Total [6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
A continuous random variable \(T\) has probability density function \(f\) defined by
\[f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t\left| {\sin 2t} \right|}}{\pi },}&{0 \leqslant t \leqslant \pi } \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\]
Sketch the graph of \(y = f(t)\).
Use your sketch to find the mode of \(T\).
Find the mean of \(T\).
Find the variance of \(T\).
Find the probability that \(T\) lies between the mean and the mode.
(i) Find \(\int_0^\pi {f(t){\text{d}}t} \) where \(0 \leqslant T \leqslant \frac{\pi }{2}\).
(ii) Hence verify that the lower quartile of \(T\) is \(\frac{\pi }{2}\).
▶️Answer/Explanation
Markscheme
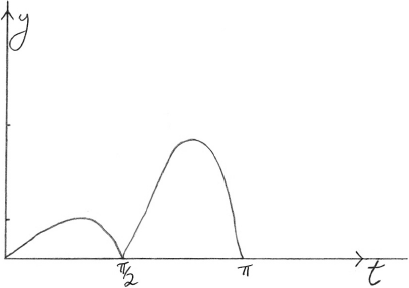
two enclosed regions (\(0 \leqslant t \leqslant \frac{\pi }{2}\) and \(\frac{\pi }{2} \leqslant t \leqslant \pi \)) bounded by the curve and the \(t\)-axis A1
correct non-symmetrical shape for \(0 \leqslant t \leqslant \frac{\pi }{2}\) and
\(\frac{\pi }{2} < {\text{mode of }}T < \pi {\text{ clearly apparent}}\) A1
[2 marks]
\({\text{mode}} = 2.46\) A1
[1 mark]
\({\text{E}}(T) = \frac{1}{\pi }\int_0^\pi {{t^2}\left| {\sin 2t} \right|{\text{d}}t} \) (M1)
\( = 2.04\) A1
[2 marks]
EITHER
\({\text{Var}}(T) = \int_0^\pi {(t – } 2.03788 \ldots {)^2}\left( {\frac{{t\left| {\sin 2t} \right|}}{\pi }} \right){\text{d}}t\) (M1)(A1)
OR
\({\text{Var}}(T) = \int_0^\pi {{t^2}} \left( {\frac{{t\left| {\sin 2t} \right|}}{\pi }} \right){\text{d}}t – {(2.03788 \ldots )^2}\)
(M1)(A1)
THEN
\({\text{Var}}(T) = 0.516\) A1
[3 marks]
\(\frac{1}{\pi }\int_{{\text{2.03788}} \ldots }^{{\text{2.456590}} \ldots } {t\left| {\sin 2t} \right|{\text{d}}t = {\text{0.285}}} \) (M1)A1
[2 marks]
(i) attempting integration by parts (M1)
\((u = t,{\text{ d}}u = {\text{d}}t,{\text{ d}}v = \sin 2t{\text{ d}}t\) and \(v = – \frac{1}{2}\cos 2t)\)
\(\frac{1}{\pi }\left[ {t\left( { – \frac{1}{2}\cos 2t} \right)} \right]_0^r – \frac{1}{\pi }\int_0^r {\left( { – \frac{1}{2}\cos 2t} \right){\text{d}}t} \) A1
Note: Award A1 if the limits are not included.
\( = \frac{{\sin 2T}}{{4\pi }} – \frac{{T\cos 2T}}{{2\pi }}\) A1
(ii) \(\frac{{\sin \pi }}{{4\pi }} – \frac{{\frac{\pi }{2}\cos \pi }}{{2\pi }} = \frac{1}{4}\) A1
as \({\text{P}}\left( {0 \leqslant T \leqslant \frac{\pi }{2}} \right) = \frac{1}{4}\) (or equivalent), then the lower quartile of \(T\) is \(\frac{\pi }{2}\) R1AG
[5 marks]
Examiners report
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
This question was generally accessible to the large majority of candidates. A substantial number of candidates were able to neatly and accurately sketch a non-symmetric bimodal continuous probability density function and to calculate its mean, mode and variance. Quite a few candidates unfortunately attempted this question with their GDC set in degrees.
Question
A random variable \(X\) has a probability distribution given in the following table.
![]()
Determine the value of \({\text{E}}({X^2})\).
Find the value of \({\text{Var}}(X)\).
▶️Answer/Explanation
Markscheme
\({\text{E}}({X^2}) = \Sigma {x^2} \bullet {\text{P}}(X = x) = 10.37{\text{ }}( = 10.4{\text{ 3 sf)}}\) (M1)A1
[2 marks]
METHOD 1
\({\text{sd}}(X) = 1.44069 \ldots \) (M1)(A1)
\({\text{Var}}(X) = 2.08{\text{ }}( = 2.0756)\) A1
METHOD 2
\({\text{E}}(X) = 2.88{\text{ }}( = 0.06 + 0.27 + 0.5 + 0.98 + 0.63 + 0.44)\) (A1)
use of \({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2}\) (M1)
Note: Award (M1) only if \({\left( {{\text{E}}(X)} \right)^2}\) is used correctly.
\(\left( {{\text{Var}}(X) = 10.37 – 8.29} \right)\)
\({\text{Var}}(X) = 2.08{\text{ }}( = 2.0756)\) A1
Note: Accept 2.11.
METHOD 3
\({\text{E}}(X) = 2.88{\text{ }}( = 0.06 + 0.27 + 0.5 + 0.98 + 0.63 + 0.44)\) (A1)
use of \({\text{Var}}(X) = {\text{E}}\left( {{{\left( {X – {\text{E}}(X)} \right)}^2}} \right)\) (M1)
\((0.679728 + \ldots + 0.549152)\)
\({\text{Var}}(E) = 2.08{\text{ }}( = 2.0756)\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
The continuous random variable X has probability density function \(f\) given by
\[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
{3ax}&,&{0 \leqslant x < 0.5} \\
{a\left( {2 – x} \right)}&,&{0.5 \leqslant x < 2} \\
0&,&{{\text{otherwise}}}
\end{array}} \right.\]
Show that \(a = \frac{2}{3}\).
Find \({\text{P}}\left( {X < 1} \right)\).
Given that \({\text{P}}\left( {s < X < 0.8} \right) = 2 \times {\text{P}}\left( {2s < X < 0.8} \right)\), and that 0.25 < s < 0.4 , find the value of s.
▶️Answer/Explanation
Markscheme
\(a\left[ {\int_0^{0.5} {3x\,{\text{d}}x} + \int_{0.5}^2 {\left( {2 – x} \right)} \,{\text{d}}x} \right] = 1\) M1
Note: Award the M1 for the total integral equalling 1, or equivalent.
\(a\left( {\frac{3}{2}} \right) = 1\) (M1)A1
\(a = \frac{2}{3}\) AG
[3 marks]
EITHER
\(\int_0^{0.5} {2x\,{\text{d}}x} + \frac{2}{3}\int_{0.5}^1 {\left( {2 – x} \right)} \,{\text{d}}x\) (M1)(A1)
\( = \frac{2}{3}\) A1
OR
\(\frac{2}{3}\int_1^2 {\left( {2 – x} \right)} \,{\text{d}}x = \frac{1}{3}\) (M1)
so \({\text{P}}\left( {X < 1} \right) = \frac{2}{3}\) (M1)A1
[3 marks]
\({\text{P}}\left( {s < X < 0.8} \right) = \int_s^{0.5} {2x\,{\text{d}}x} + \frac{2}{3}\int_{0.5}^{0.8} {\left( {2 – x} \right)} \,{\text{d}}x\) M1A1
\( = \left[ {{x^2}} \right]_s^{0.5} + 0.27\)
\(0.25 – {s^2} + 0.27\) (A1)
\({\text{P}}\left( {2s < X < 0.8} \right) = \frac{2}{3}\int_{2s}^{0.8} {\left( {2 – x} \right)} \,{\text{d}}x\) A1
\( = \frac{2}{3}\left[ {2x – \frac{{{x^2}}}{2}} \right]_{2s}^{0.8}\)
\(\frac{2}{3}\left( {1.28 – \left( {4s – 2{s^2}} \right)} \right)\)
equating
\(0.25 – {s^2} + 0.27 = \frac{4}{3}\left( {1.28 – \left( {4s – 2{s^2}} \right)} \right)\) (A1)
attempt to solve for s (M1)
s = 0.274 A1
[7 marks]
