IBDP Maths SL 5.4 Tangents and normals at a given point, and their equations AA HL Paper 2- Exam Style Questions- New Syllabus
Question
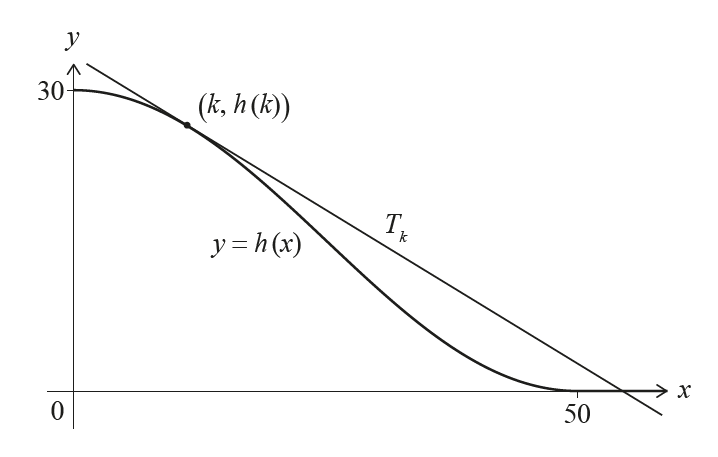
Syllabus Topic Codes (IB Mathematics AA HL):
• SL 5.3: Derivative of \( \cos x \) — part (a)
• SL 5.4: Tangents and normals at a given point— part (a)
• SL 5.6: The chain rule for composite functions — part (a)
▶️ Answer/Explanation
(a)
The gradient of the tangent is \( h'(k) \).
Differentiate \( h(x) \):
\( h'(x) = 15 \cdot \left( -\sin\left( \frac{\pi x}{50} \right) \right) \cdot \frac{\pi}{50} = -\frac{15\pi}{50} \sin\left( \frac{\pi x}{50} \right) \)
Simplify: \( -\frac{3\pi}{10} \sin\left( \frac{\pi x}{50} \right) \).
At \( x = k \):
\( h'(k) = -\frac{3\pi}{10} \sin\left( \frac{\pi k}{50} \right) \)
\( \boxed{-\frac{3\pi}{10} \sin\left( \frac{\pi k}{50} \right)} \)
(b)
If the angle between \( T_k \) and the positive \( x \)-axis is \( \frac{\pi}{8} \), then the gradient \( m = \tan\left( \frac{\pi}{8} \right) \).
Since \( h'(k) \) is negative for most \( k \) in the domain, and \( \tan(\pi/8) > 0 \), we consider the supplementary angle: the gradient could be \( \tan\left( \pi – \frac{\pi}{8} \right) = \tan\left( \frac{7\pi}{8} \right) \), which is negative.
Set \( h'(k) = \tan\left( \frac{7\pi}{8} \right) \):
\( -\frac{3\pi}{10} \sin\left( \frac{\pi k}{50} \right) = \tan\left( \frac{7\pi}{8} \right) \)
\( \sin\left( \frac{\pi k}{50} \right) = -\frac{10}{3\pi} \tan\left( \frac{7\pi}{8} \right) \)
Calculate: \( \tan(7\pi/8) = \tan(157.5^\circ) \approx -0.414214 \)
RHS \( \approx -\frac{10}{3\pi} (-0.414214) \approx 0.43923 \)
So \( \sin\left( \frac{\pi k}{50} \right) \approx 0.43923 \)
\( \frac{\pi k}{50} \approx \arcsin(0.43923) \approx 0.4548 \) or \( \pi – 0.4548 \approx 2.6868 \)
Thus \( k \approx \frac{50}{\pi} \times 0.4548 \approx 7.242 \) or \( k \approx \frac{50}{\pi} \times 2.6868 \approx 42.758 \)
Rounded to three significant figures:
\( \boxed{k = 7.24} \), \( \boxed{k = 42.8} \)
