Question
Consider the function f defined by f (x) = 90e-0.5x for x ∈ R+ The graph of f and the line y = x intersect at point P.
Find the x-coordinate of P. [2]
The line L has a gradient of –1 and is a tangent to the graph of f at the point Q.
Find the exact coordinates of Q. [4]
Show that the equation of L is y = -x + 2ln45 + 2 . [2]
The shaded region A is enclosed by the graph of f and the lines y = x and L .
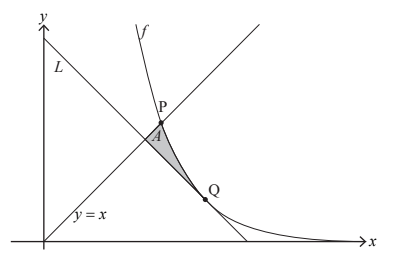
(i) Find the x-coordinate of the point where L intersects the line y = x .
(ii) Hence, find the area of A . [5]
The line L is tangent to the graphs of both f and the inverse function f –1 .
Find the shaded area enclosed by the graphs of f and f –1 and the line L . [2]
▶️Answer/Explanation
Ans:
(a)
attempt to find the point of intersection of the graph of f and the line y = x
x = 5.56619… = 5.57
(b)
\(f'(x)=-45e^{-0.5x}\)
attempt to set the gradient of equal to -1
-45e -0.5x = -1
Q has coordinates \((2ln45,2) \)or \((-2 ln\frac{1}{45},2)\)
(c)
attempt to substitute coordinates of Q ( in any order) into an appropriate equation
y-2= -(x-2ln45)
OR
2= – 2 ln 45 + C
equation of L is y = – x+ 2ln 45 + 2
(d)
(i) x= ln45 + 1 (=4.81)
(ii) appropriate method to find the sum of two areas using integrals of the difference of two functions 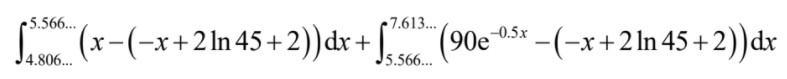
=1.51965… =1.52
(e) by symmetry 2 ×1.52
= 3.03930… = 3.04
Question
A family of cubic functions is defined as \({f_k}(x) = {k^2}{x^3} – k{x^2} + x,{\text{ }}k \in {\mathbb{Z}^ + }\) .
(a) Express in terms of k
(i) \({{f’}_k}(x){\text{ and }}{{f”}_k}(x)\) ;
(ii) the coordinates of the points of inflexion \({P_k}\) on the graphs of \({f_k}\) .
(b) Show that all \({P_k}\) lie on a straight line and state its equation.
(c) Show that for all values of k, the tangents to the graphs of \({f_k}\) at \({P_k}\) are parallel, and find the equation of the tangent lines.
▶️Answer/Explanation
Markscheme
(a) (i) \({{f’}_k}(x) = 3{k^2}{x^2} – 2kx + 1\) A1
\({{f”}_k}(x) = 6{k^2}x – 2k\) A1
(ii) Setting \(f”(x) = 0\) M1
\( \Rightarrow 6{k^2}x – 2k = 0 \Rightarrow x = \frac{1}{{3k}}\) A1
\(f\left( {\frac{1}{{3k}}} \right) = {k^2}{\left( {\frac{1}{{3k}}} \right)^3} – k{\left( {\frac{1}{{3k}}} \right)^2} + \left( {\frac{1}{{3k}}} \right)\) M1
\( = \frac{7}{{27k}}\) A1
Hence, \({P_k}{\text{ is }}\left( {\frac{1}{{3k}},\frac{7}{{27k}}} \right)\)
[6 marks]
(b) Equation of the straight line is \(y = \frac{7}{9}x\) A1
As this equation is independent of k, all \({P_k}\) lie on this straight line R1
[2 marks]
(c) Gradient of tangent at \({P_k}\) :
\(f'({P_k}) = f’\left( {\frac{1}{{3k}}} \right) = 3{k^2}{\left( {\frac{1}{{3k}}} \right)^2} – 2k\left( {\frac{1}{{3k}}} \right) + 1 = \frac{2}{3}\) M1A1
As the gradient is independent of k, the tangents are parallel. R1
\(\frac{7}{{27k}} = \frac{2}{3} \times \frac{1}{{3k}} + c \Rightarrow c = \frac{1}{{27k}}\) (A1)
The equation is \(y = \frac{2}{3}x + \frac{1}{{27k}}\) A1
[5 marks]
Total [13 marks]
Question
Let \(f\) be a function defined by \(f(x) = x + 2\cos x\) , \(x \in \left[ {0,{\text{ }}2\pi } \right]\) . The diagram below shows a region \(S\) bound by the graph of \(f\) and the line \(y = x\) .
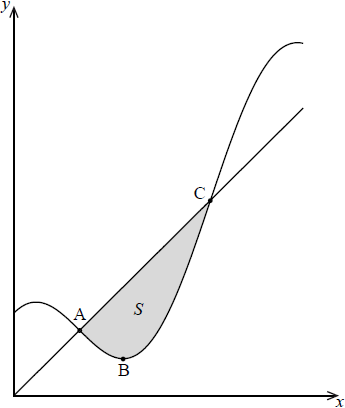
A and C are the points of intersection of the line \(y = x\) and the graph of \(f\) , and B is the minimum point of \(f\) .
(a) If A, B and C have x-coordinates \(a\frac{\pi }{2}\), \(b\frac{\pi }{6}\) and \(c\frac{\pi }{2}\), where \(a\) , \(b\), \(c \in \mathbb{N}\) , find the values of \(a\) , \(b\) and \(c\) .
(b) Find the range of \(f\) .
(c) Find the equation of the normal to the graph of f at the point C, giving your answer in the form \(y = px + q\) .
(d) The region \(S\) is rotated through \({2\pi }\) about the x-axis to generate a solid.
(i) Write down an integral that represents the volume \(V\) of this solid.
(ii) Show that \(V = 6{\pi ^2}\) .
▶️Answer/Explanation
Markscheme
(a) METHOD 1
using GDC
\(a = 1\), \(b = 5\), \(c = 3\) A1A2A1
METHOD 2
\(x = x + 2\cos x \Rightarrow \cos x = 0\)
\( \Rightarrow x = \frac{\pi }{2}\), \(\frac{{3\pi }}{2}\) … M1
\(a = 1\), \(c = 3\) A1
\(1 – 2\sin x = 0\) M1
\( \Rightarrow \sin x = \frac{1}{2} \Rightarrow x = \frac{\pi }{6}\) or \(\frac{{5\pi }}{6}\)
\(b = 5\) A1
Note: Final M1A1 is independent of previous work.
[4 marks]
(b) \(f\left( {\frac{{5\pi }}{6}} \right) = \frac{{5\pi }}{6} – \sqrt 3 \) (or \(0.886\)) (M1)
\(f(2\pi ) = 2\pi + 2\) (or \(8.28\)) (M1)
the range is \(\left[ {\frac{{5\pi }}{6} – \sqrt 3 ,{\text{ }}2\pi + 2} \right]\) (or [\(0.886\), \(8.28\)]) A1
[3 marks]
(c) \(f'(x) = 1 – 2\sin x\) (M1)
\(f’\left( {\frac{{3\pi }}{6}} \right) = 3\) A1
gradient of normal \( = – \frac{1}{3}\) (M1)
equation of the normal is \(y – \frac{{3\pi }}{2} = – \frac{1}{3}\left( {x – \frac{{3\pi }}{2}} \right)\) (M1)
\(y = – \frac{1}{3}x + 2\pi \) (or equivalent decimal values) A1 N4
[5 marks]
(d) (i) \(V = \pi \int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( {{x^2} – {{\left( {x + 2\cos x} \right)}^2}} \right)} {\text{d}}x\) (or equivalent) A1A1
Note: Award A1 for limits and A1 for \(\pi \) and integrand.
(ii) \(V = \pi \int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( {{x^2} – {{\left( {x + 2\cos x} \right)}^2}} \right)} {\text{d}}x\)
\( = – \pi \int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {\left( {4x\cos x + 4{{\cos }^2}x} \right)} {\text{d}}x\)
using integration by parts M1
and the identity \(4{\cos ^2}x = 2\cos 2x + 2\) , M1
\(V = – \pi \left[ {\left( {4x\sin x + 4\cos x} \right) + \left( {\sin 2x + 2x} \right)} \right]_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}}\) A1A1
Note: Award A1 for \({4x\sin x + 4\cos x}\) and A1 for sin \({2x + 2x}\) .
\( = – \pi \left[ {\left( {6\pi \sin \frac{{3\pi }}{2} + 4\cos \frac{{3\pi }}{2} + \sin 3\pi + 3\pi } \right) – \left( {2\pi sin\frac{\pi }{2} + 4\cos \frac{\pi }{2} + \sin \pi + \pi } \right)} \right]\) A1
\( = – \pi \left( { – 6\pi + 3\pi – \pi } \right)\)
\( = 6{\pi ^2}\) AG N0
Note: Do not accept numerical answers.
[7 marks]
Total [19 marks]
Examiners report
Generally there were many good attempts to this, more difficult, question. A number of students found \(b\) to be equal to 1, rather than 5. In the final part few students could successfully work through the entire integral successfully.
Question
Find the equation of the normal to the curve \({x^3}{y^3} – xy = 0\) at the point (1, 1).
▶️Answer/Explanation
Markscheme
\({x^3}{y^3} – xy = 0\)
\(3{x^2}{y^3} + 3{x^3}{y^2}y’ – y – xy’ = 0\)
Note: Award A1 for correctly differentiating each term.
\(x = 1,{\text{ }}y = 1\) \(3 + 3y’ – 1 – y’ = 0\)
\(2y’ = – 2\)
\(y’ = – 1\) (M1)A1
gradient of normal = 1 (A1)
equation of the normal \(y – 1 = x – 1\) A1 N2
\(y = x\)
Note: Award A2R5 for correct answer and correct justification.
[7 marks]
Examiners report
This implicit differentiation question was well answered by most candidates with many achieving full marks. Some candidates made algebraic errors which prevented them from scoring well in this question.
Other candidates realised that the equation of the curve could be simplified although the simplification was seldom justified.
Question
The line \(y = m(x – m)\) is a tangent to the curve \((1 – x)y = 1\).
Determine m and the coordinates of the point where the tangent meets the curve.
▶️Answer/Explanation
Markscheme
EITHER
\(y = \frac{1}{{1 – x}} \Rightarrow y’ = \frac{1}{{{{(1 – x)}^2}}}\) M1A1
solve simultaneously M1
\(\frac{1}{{1 – x}} = m(x – m){\text{ and }}\frac{1}{{{{(1 – x)}^2}}} = m\)
\(\frac{1}{{1 – x}} = \frac{1}{{{{(1 – x)}^2}}}\left( {x – \frac{1}{{{{(1 – x)}^2}}}} \right)\) A1
Note: Accept equivalent forms.
\({(1 – x)^3} – x{(1 – x)^2} + 1 = 0,{\text{ }}x \ne 1\)
\(x = 1.65729 \ldots \Rightarrow y = \frac{1}{{1 – 1.65729 \ldots }} = – 1.521379 \ldots \)
tangency point (1.66, –1.52) A1A1
\(m = {( – 1.52137 \ldots )^2} = 2.31\) A1
OR
\((1 – x)y = 1\)
\(m(1 – x)(x – m) = 1\) M1
\(m(x – {x^2} – m + mx) = 1\)
\(m{x^2} – x(m + {m^2}) + ({m^2} + 1) = 0\) A1
\({b^2} – 4ac = 0\) (M1)
\({(m + {m^2})^2} – 4m({m^2} + 1) = 0\)
\(m = 2.31\) A1
substituting \(m = 2.31 \ldots {\text{ into }}m{x^2} – x(m + {m^2}) + ({m^2} + 1) = 0\) (M1)
\(x = 1.66\) A1
\(y = \frac{1}{{1 – 1.65729}} = – 1.52\) A1
tangency point (1.66, –1.52)
[7 marks]
Examiners report
Very few candidates answered this question well but among those a variety of nice approaches were seen. This question required some organized thinking and good understanding of the concepts involved and therefore just strong candidates were able to go beyond the first steps. Sadly a few good answers were spoiled due to early rounding.
Question
A function \(f\) is defined by \(f(x) = \frac{1}{2}\left( {{{\text{e}}^x} + {{\text{e}}^{ – x}}} \right),{\text{ }}x \in \mathbb{R}\).
a.(i) Explain why the inverse function \({f^{ – 1}}\) does not exist.
(ii) Show that the equation of the normal to the curve at the point P where \(x = \ln 3\) is given by \(9x + 12y – 9\ln 3 – 20 = 0\).
(iii) Find the x-coordinates of the points Q and R on the curve such that the tangents at Q and R pass through \({\text{(0, 0)}}\).[14]
b.The domain of \(f\) is now restricted to \(x \geqslant 0\).
(i) Find an expression for \({f^{ – 1}}(x)\).
(ii) Find the volume generated when the region bounded by the curve \(y = f(x)\) and the lines \(x = 0\) and \(y = 5\) is rotated through an angle of \(2\pi \) radians about the y-axis.[8]
▶️Answer/Explanation
Markscheme
(i) either counterexample or sketch or
recognising that \(y = k{\text{ }}(k > 1)\) intersects the graph of \(y = f(x)\) twice M1
function is not \(1 – 1\) (does not obey horizontal line test) R1
so \({f^{ – 1}}\) does not exist AG
(ii) \(f'(x) = \frac{1}{2}\left( {{{\text{e}}^x} – {{\text{e}}^{ – x}}} \right)\) (A1)
\(f'(\ln 3) = \frac{4}{3}{\text{ }}( = 1.33)\) (A1)
\(m = – \frac{3}{4}\) M1
\(f(\ln 3) = \frac{5}{3}{\text{ }}( = 1.67)\) A1
EITHER
\(\frac{{y – \frac{5}{3}}}{{x – \ln 3}} = – \frac{3}{4}\) M1
\(4y – \frac{{20}}{3} = – 3x + 3\ln 3\) A1
OR
\(\frac{5}{3} = – \frac{3}{4}\ln 3 + c\) M1
\(c = \frac{5}{3} + \frac{3}{4}\ln 3\)
\(y = – \frac{3}{4}x + \frac{5}{3} + \frac{3}{4}\ln 3\) A1
\(12y = – 9x + 20 + 9\ln 3\)
THEN
\(9x + 12y – 9\ln 3 – 20 = 0\) AG
(iii) The tangent at \(\left( {a,{\text{ }}f(a)} \right)\) has equation \(y – f(a) = f'(a)(x – a)\). (M1)
\(f'(a) = \frac{{f(a)}}{a}\) (or equivalent) (A1)
\({{\text{e}}^a} – {{\text{e}}^{ – a}} = \frac{{{{\text{e}}^a} + {{\text{e}}^{ – a}}}}{a}\) (or equivalent) A1
attempting to solve for a (M1)
\(a = \pm 1.20\) A1A1
[14 marks]
(i) \(2y = {{\text{e}}^x} + {{\text{e}}^{ – x}}\)
\({{\text{e}}^{2x}} – 2y{{\text{e}}^x} + 1 = 0\) M1A1
Note: Award M1 for either attempting to rearrange or interchanging x and y.
\({{\text{e}}^x} = \frac{{2y \pm \sqrt {4{y^2} – 4} }}{2}\) A1
\({{\text{e}}^x} = y \pm \sqrt {{y^2} – 1} \)
\(x = \ln \left( {y \pm \sqrt {{y^2} – 1} } \right)\) A1
\({f^{ – 1}}(x) = \ln \left( {x + \sqrt {{x^2} – 1} } \right)\) A1
Note: Award A1 for correct notation and for stating the positive “branch”.
(ii) \(V = \pi \int_1^5 {{{\left( {\ln \left( {y + \sqrt {{y^2} – 1} } \right)} \right)}^2}{\text{d}}y} \) (M1)(A1)
Note: Award M1 for attempting to use \(V = \pi \int_c^d {{x^2}{\text{d}}y} \).
\( = 37.1{\text{ }}\left( {{\text{unit}}{{\text{s}}^3}} \right)\) A1
[8 marks]
Examiners report
In part (a) (i), successful candidates typically sketched the graph of \(y = f(x)\), applied the horizontal line test to the graph and concluded that the function was not \(1 – 1\) (it did not obey the horizontal line test).
In part (a) (ii), a large number of candidates were able to show that the equation of the normal at point P was \(9x + 12y – 9\ln 3 – 20 = 0\). A few candidates used the gradient of the tangent rather than using it to find the gradient of the normal.
Part (a) (iii) challenged most candidates. Most successful candidates graphed \(y = f(x)\) and \(y = xf'(x)\) on the same set of axes and found the x-coordinates of the intersection points.
Part (b) (i) challenged most candidates. While a large number of candidates seemed to understand how to find an inverse function, poor algebra skills (e.g. erroneously taking the natural logarithm of both sides) meant that very few candidates were able to form a quadratic in either \({{\text{e}}^x}\) or \({{\text{e}}^y}\).
Question
Find the equation of the normal to the curve \(y = \frac{{{{\text{e}}^x}\cos x\ln (x + {\text{e}})}}{{{{({x^{17}} + 1)}^5}}}\) at the point where \(x = 0\).
In your answer give the value of the gradient, of the normal, to three decimal places.
▶️Answer/Explanation
Markscheme
\(x = 0 \Rightarrow y = 1\) (A1)
\(y'(0) = 1.367879 \ldots \) (M1)(A1)
Note: The exact answer is \(y'(0) = \frac{{{\text{e}} + 1}}{{\text{e}}} = 1 + \frac{1}{{\text{e}}}\).
so gradient of normal is \(\frac{{ – 1}}{{1.367879 \ldots }}\;\;\;( = – 0.731058 \ldots )\) (M1)(A1)
equation of normal is \(y = – 0.731058 \ldots x + c\) (M1)
gives \(y = – 0.731x + 1\) A1
Note: The exact answer is \(y = – \frac{{\text{e}}}{{{\text{e}} + 1}}x + 1\).
Accept \(y – 1 = – 0.731058 \ldots (x – 0)\)
[7 marks]
Examiners report
Surprisingly many candidates ignored that fact that paper 2 is a calculator paper, attempted an algebraic approach and wasted lots of time. Candidates that used the GDC were in general successful and achieved 7/7. A number of candidates either found the equation of the tangent or used the positive reciprocal for the normal and many did not find the value of \(y\) corresponding to \(f(0)\).
Question
The function f is defined on the domain [0, 2] by \(f(x) = \ln (x + 1)\sin (\pi x)\) .
a.Obtain an expression for \(f'(x)\) .[3]
b.Sketch the graphs of f and \(f’\) on the same axes, showing clearly all x-intercepts.[4]
c.Find the x-coordinates of the two points of inflexion on the graph of f .[2]
d.Find the equation of the normal to the graph of f where x = 0.75 , giving your answer in the form y = mx + c .[3]
e.Consider the points \({\text{A}}\left( {a{\text{ }},{\text{ }}f(a)} \right)\) , \({\text{B}}\left( {b{\text{ }},{\text{ }}f(b)} \right)\) and \({\text{C}}\left( {c{\text{ }},{\text{ }}f(c)} \right)\)
where a , b and c \((a < b < c)\) are the solutions of the equation \(f(x) = f'(x)\) . Find the area of the triangle ABC. [6]
▶️Answer/Explanation
Markscheme
\(f'(x) = \frac{1}{{x + 1}}\sin (\pi x) + \pi \ln (x + 1)\cos (\pi x)\) M1A1A1
[3 marks]
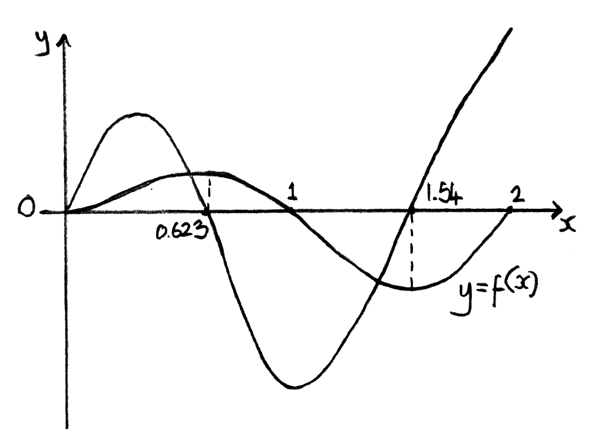 A4
A4
Note: Award A1A1 for graphs, A1A1 for intercepts.
[4 marks]
0.310, 1.12 A1A1
[2 marks]
\(f'(0.75) = – 0.839092\) A1
so equation of normal is \(y – 0.39570812 = \frac{1}{{0.839092}}(x – 0.75)\) M1
\(y = 1.19x – 0.498\) A1
[3 marks]
\({\text{A}}(0,{\text{ }}0)\)
\({\text{B(}}\overbrace {0.548 \ldots }^c,\overbrace {0.432 \ldots }^d)\) A1
\({\text{C(}}\overbrace {1.44 \ldots }^e,\overbrace { – 0.881 \ldots }^f)\) A1
Note: Accept coordinates for B and C rounded to 3 significant figures.
area \(\Delta {\text{ABC}} = \frac{1}{2}|\)(ci + dj) \( \times \) (ei + fj)\(|\) M1A1
\( = \frac{1}{2}(de – cf)\) A1
\( = 0.554\) A1
[6 marks]
