IBDP Maths SL 5.2 Increasing and decreasing functions AA HL Paper 1- Exam Style Questions- New Syllabus
▶️ Answer/Explanation
EITHER
derivative of \( \frac{x}{{1 – x}} \) is \( \frac{{(1 – x) – x( – 1)}}{{{{(1 – x)}^2}}} \) M1A1
\( f'(x) = \frac{1}{2}{\left( {\frac{x}{{1 – x}}} \right)^{ – \frac{1}{2}}}\frac{1}{{{{(1 – x)}^2}}} \) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}} \) AG
\( f'(x) > 0 \) (for all \( 0 < x < 1 \)) so the function is increasing R1
OR
\( f(x) = \frac{{{x^{\frac{1}{2}}}}}{{{{(1 – x)}^{\frac{1}{2}}}}} \)
\( f'(x) = \frac{{{{(1 – x)}^{\frac{1}{2}}}\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \frac{1}{2}{x^{\frac{1}{2}}}{{(1 – x)}^{ – \frac{1}{2}}}( – 1)}}{{1 – x}} \) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{1}{2}}} + \frac{1}{2}{x^{\frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}} \) A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}[1 – x + x] \) M1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}} \) AG
\( f'(x) > 0 \) (for all \( 0 < x < 1 \)) so the function is increasing R1
[5 marks]
\( f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}} \)
\( \Rightarrow f”(x) = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{3}{2}}} + \frac{3}{4}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{5}{2}}} \) M1A1
\( = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{5}{2}}}[1 – 4x] \)
\( f”(x) = 0 \Rightarrow x = \frac{1}{4} \) M1A1
\( f”(x) \) changes sign at \( x = \frac{1}{4} \) hence there is a point of inflexion R1
\( x = \frac{1}{4} \Rightarrow y = \frac{1}{{\sqrt 3 }} \) A1
the coordinates are \( \left( {\frac{1}{4},\frac{1}{{\sqrt 3 }}} \right) \)
[6 marks]
\( x = {\sin ^2}\theta \Rightarrow \frac{{{\text{d}}x}}{{{\text{d}}\theta }} = 2\sin \theta \cos \theta \) M1A1
\( \int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \int {\sqrt {\frac{{{{\sin }^2}\theta }}{{1 – {{\sin }^2}\theta }}} 2\sin \theta \cos \theta {\text{d}}\theta } } \) M1A1
\( = \int {2{{\sin }^2}\theta {\text{d}}\theta } \) A1
\( = \int {1 – \cos 2\theta } {\text{d}}\theta \) M1A1
\( = \theta – \frac{1}{2}\sin 2\theta + c \) A1
\( \theta = \arcsin \sqrt x \) A1
\( \frac{1}{2}\sin 2\theta = \sin \theta \cos \theta = \sqrt x \sqrt {1 – x} = \sqrt {x – {x^2}} \) M1A1
hence \( \int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \arcsin \sqrt x } – \sqrt {x – {x^2}} + c \) AG
[11 marks]
▶️ Answer/Explanation
(i) \(x = {{\text{e}}^{3y + 1}}\) M1
taking the natural logarithm of both sides and attempting to transpose M1
\(\left( {{f^{ – 1}}(x)} \right) = \frac{1}{3}(\ln x – 1)\) A1
(ii) \(x \in {\mathbb{R}^ + }\) or equivalent, for example \(x > 0\). A1
\(\boxed{\dfrac{1}{3}(\ln x – 1),\; x \in \mathbb{R}^+}\)
\(\ln x = \frac{1}{3}(\ln x – 1) \Rightarrow \ln x – \frac{1}{3}\ln x = -\frac{1}{3}\) (or equivalent) M1A1
\(\ln x = -\frac{1}{2}\) (or equivalent) A1
\(x = {{\text{e}}^{-\frac{1}{2}}}\) A1
coordinates of \(P\) are \(\left( {{{\text{e}}^{-\frac{1}{2}}}, -\frac{1}{2}} \right)\) A1
\(\boxed{\left( e^{-\frac{1}{2}}, -\frac{1}{2} \right)}\)
coordinates of \(Q\) are (\(1, 0\)) seen anywhere A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{x}\) M1
at \({\text{Q}}, \frac{{{\text{d}}y}}{{{\text{d}}x}} = 1\) A1
\(y = x – 1\) AG
\(\boxed{y = x – 1}\)
let the required area be \(A\)
\(A = \int_1^e {x – 1{\text{d}}x – \int_1^e {\ln x{\text{d}}x} }\) M1
attempting to use integration by parts to find \(\int {\ln x{\text{d}}x}\) M1
\(= \left[ {\frac{{{x^2}}}{2} – x} \right]_1^{\text{e}} – [x\ln x – x]_1^{\text{e}}\) A1A1
\(= \frac{{{{\text{e}}^2}}}{2} – {\text{e}} – \frac{1}{2}\left( {= \frac{{{{\text{e}}^2} – 2{\text{e}} – 1}}{2}} \right)\) A1
\(\boxed{\dfrac{e^2 – 2e – 1}{2}}\)
(i) METHOD 1
consider \(h(x) = x – 1 – \ln x\)
\(h(1) = 0\) and \(h'(x) = 1 – \frac{1}{x}\) A1
as \(h'(x) \ge 0\) for \(x \ge 1\), then \(h(x) \ge 0\) for \(x \ge 1\) R1
as \(h'(x) \le 0\) for \(0 < x \le 1\), then \(h(x) \ge 0\) for \(0 < x \le 1\) R1
so \(g(x) \le x – 1, x \in {\mathbb{R}^ + }\) AG
METHOD 3
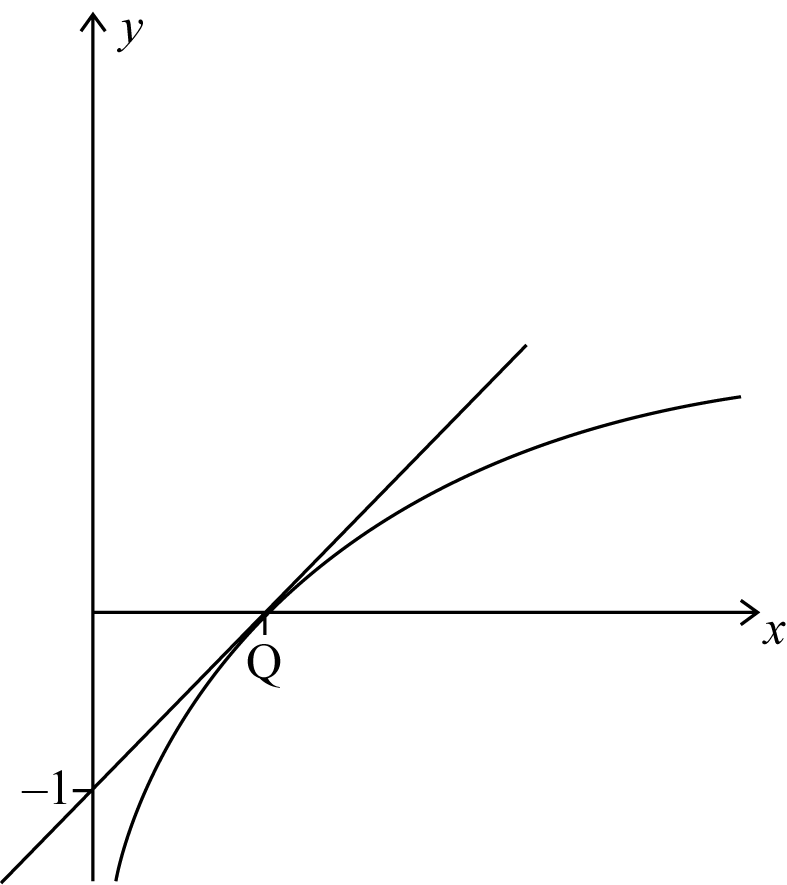
clear correct graphs of \(y = x – 1\) and \(\ln x\) for \(x > 0\) A1A1
statement to the effect that the graph of \(\ln x\) is below the graph of its tangent at \(x = 1\) R1AG
(ii) replacing \(x\) by \(\frac{1}{x}\) to obtain \(\ln \left( {\frac{1}{x}} \right) \le \frac{1}{x} – 1\) M1
\(- \ln x \le \frac{1}{x} – 1\) A1
\(\ln x \ge 1 – \frac{1}{x}\left( {= \frac{{x – 1}}{x}} \right)\) A1
so \(\frac{{x – 1}}{x} \le g(x), x \in {\mathbb{R}^ + }\) AG
\(\boxed{\text{See proof above}}\)
—Markscheme—
(i) \(x = {{\text{e}}^{3y + 1}}\) M1
taking the natural logarithm of both sides and attempting to transpose M1
\(\left( {{f^{ – 1}}(x)} \right) = \frac{1}{3}(\ln x – 1)\) A1
(ii) \(x \in {\mathbb{R}^ + }\) or equivalent, for example \(x > 0\). A1
[4 marks]
\(\ln x = \frac{1}{3}(\ln x – 1) \Rightarrow \ln x – \frac{1}{3}\ln x = -\frac{1}{3}\) (or equivalent) M1A1
\(\ln x = -\frac{1}{2}\) (or equivalent) A1
\(x = {{\text{e}}^{-\frac{1}{2}}}\) A1
coordinates of \(P\) are \(\left( {{{\text{e}}^{-\frac{1}{2}}}, -\frac{1}{2}} \right)\) A1
[5 marks]
coordinates of \(Q\) are (\(1, 0\)) seen anywhere A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{x}\) M1
at \({\text{Q}}, \frac{{{\text{d}}y}}{{{\text{d}}x}} = 1\) A1
\(y = x – 1\) AG
[3 marks]
let the required area be \(A\)
\(A = \int_1^e {x – 1{\text{d}}x – \int_1^e {\ln x{\text{d}}x} }\) M1
attempting to use integration by parts to find \(\int {\ln x{\text{d}}x}\) M1
\(= \left[ {\frac{{{x^2}}}{2} – x} \right]_1^{\text{e}} – [x\ln x – x]_1^{\text{e}}\) A1A1
\(= \frac{{{{\text{e}}^2}}}{2} – {\text{e}} – \frac{1}{2}\left( {= \frac{{{{\text{e}}^2} – 2{\text{e}} – 1}}{2}} \right)\) A1
[5 marks]
(i) METHOD 1
consider \(h(x) = x – 1 – \ln x\)
\(h(1) = 0\) and \(h'(x) = 1 – \frac{1}{x}\) A1
as \(h'(x) \ge 0\) for \(x \ge 1\), then \(h(x) \ge 0\) for \(x \ge 1\) R1
as \(h'(x) \le 0\) for \(0 < x \le 1\), then \(h(x) \ge 0\) for \(0 < x \le 1\) R1
so \(g(x) \le x – 1, x \in {\mathbb{R}^ + }\) AG
(ii) replacing \(x\) by \(\frac{1}{x}\) to obtain \(\ln \left( {\frac{1}{x}} \right) \le \frac{1}{x} – 1\) M1
\(- \ln x \le \frac{1}{x} – 1\) A1
\(\ln x \ge 1 – \frac{1}{x}\left( {= \frac{{x – 1}}{x}} \right)\) A1
so \(\frac{{x – 1}}{x} \le g(x), x \in {\mathbb{R}^ + }\) AG
[6 marks]