Question
Let \(f(x) = \sqrt {\frac{x}{{1 – x}}} ,{\text{ }}0 < x < 1\).
a.Show that \(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) and deduce that f is an increasing function.[5]
b.Show that the curve \(y = f(x)\) has one point of inflexion, and find its coordinates.[6]
c. Use the substitution \(x = {\sin ^2}\theta \) to show that \(\int {f(x){\text{d}}x} = \arcsin \sqrt x – \sqrt {x – {x^2}} + c\) .[11]
▶️Answer/Explanation
Markscheme
EITHER
derivative of \(\frac{x}{{1 – x}}\) is \(\frac{{(1 – x) – x( – 1)}}{{{{(1 – x)}^2}}}\) M1A1
\(f'(x) = \frac{1}{2}{\left( {\frac{x}{{1 – x}}} \right)^{ – \frac{1}{2}}}\frac{1}{{{{(1 – x)}^2}}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
OR
\(f(x) = \frac{{{x^{\frac{1}{2}}}}}{{{{(1 – x)}^{\frac{1}{2}}}}}\)
\(f'(x) = \frac{{{{(1 – x)}^{\frac{1}{2}}}\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \frac{1}{2}{x^{\frac{1}{2}}}{{(1 – x)}^{ – \frac{1}{2}}}( – 1)}}{{1 – x}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{1}{2}}} + \frac{1}{2}{x^{\frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}[1 – x + x]\) M1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
[5 marks]
\(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\)
\( \Rightarrow f”(x) = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{3}{2}}} + \frac{3}{4}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{5}{2}}}\) M1A1
\( = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{5}{2}}}[1 – 4x]\)
\(f”(x) = 0 \Rightarrow x = \frac{1}{4}\) M1A1
\(f”(x)\) changes sign at \(x = \frac{1}{4}\) hence there is a point of inflexion R1
\(x = \frac{1}{4} \Rightarrow y = \frac{1}{{\sqrt 3 }}\) A1
the coordinates are \(\left( {\frac{1}{4},\frac{1}{{\sqrt 3 }}} \right)\)
[6 marks]
\(x = {\sin ^2}\theta \Rightarrow \frac{{{\text{d}}x}}{{{\text{d}}\theta }} = 2\sin \theta \cos \theta \) M1A1
\(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \int {\sqrt {\frac{{{{\sin }^2}\theta }}{{1 – {{\sin }^2}\theta }}} 2\sin \theta \cos \theta {\text{d}}\theta } } \) M1A1
\( = \int {2{{\sin }^2}\theta {\text{d}}\theta } \) A1
\( = \int {1 – \cos 2\theta } {\text{d}}\theta \) M1A1
\( = \theta – \frac{1}{2}\sin 2\theta + c\) A1
\(\theta = \arcsin \sqrt x \) A1
\(\frac{1}{2}\sin 2\theta = \sin \theta \cos \theta = \sqrt x \sqrt {1 – x} = \sqrt {x – {x^2}} \) M1A1
hence \(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \arcsin \sqrt x } – \sqrt {x – {x^2}} + c\) AG
[11 marks]
Examiners report
Part (a) was generally well done, although few candidates made the final deduction asked for. Those that lost other marks in this part were generally due to mistakes in algebraic manipulation. In part (b) whilst many students found the second derivative and set it equal to zero, few then confirmed that it was a point of inflexion. There were several good attempts for part (c), even though there were various points throughout the question that provided stopping points for other candidates.
Part (a) was generally well done, although few candidates made the final deduction asked for. Those that lost other marks in this part were generally due to mistakes in algebraic manipulation. In part (b) whilst many students found the second derivative and set it equal to zero, few then confirmed that it was a point of inflexion. There were several good attempts for part (c), even though there were various points throughout the question that provided stopping points for other candidates.
Part (a) was generally well done, although few candidates made the final deduction asked for. Those that lost other marks in this part were generally due to mistakes in algebraic manipulation. In part (b) whilst many students found the second derivative and set it equal to zero, few then confirmed that it was a point of inflexion. There were several good attempts for part (c), even though there were various points throughout the question that provided stopping points for other candidates.
Question
The function \(f\) is defined as \(f(x) = {{\text{e}}^{3x + 1}},{\text{ }}x \in \mathbb{R}\).
a.(i) Find \({f^{ – 1}}(x)\).
(ii) State the domain of \({f^{ – 1}}\).[4]
The function \(g\) is defined as \(g(x) = \ln x,{\text{ }}x \in {\mathbb{R}^ + }\).
The graph of \(y = g(x)\) and the graph of \(y = {f^{ – 1}}(x)\) intersect at the point \(P\).
Find the coordinates of \(P\).[5]
c.The graph of \(y = g(x)\) intersects the \(x\)-axis at the point \(Q\).
Show that the equation of the tangent \(T\) to the graph of \(y = g(x)\) at the point \(Q\) is \(y = x – 1\).[3]
A region \(R\) is bounded by the graphs of \(y = g(x)\), the tangent \(T\) and the line \(x = {\text{e}}\).
Find the area of the region \(R\).[5]
A region \(R\) is bounded by the graphs of \(y = g(x)\), the tangent \(T\) and the line \(x = {\text{e}}\).
(i) Show that \(g(x) \le x – 1,{\text{ }}x \in {\mathbb{R}^ + }\).
(ii) By replacing \(x\) with \(\frac{1}{x}\) in part (e)(i), show that \(\frac{{x – 1}}{x} \le g(x),{\text{ }}x \in {\mathbb{R}^ + }\).[6]
▶️Answer/Explanation
Markscheme
(i) \(x = {{\text{e}}^{3y + 1}}\) M1
Note: The M1 is for switching variables and can be awarded at any stage.
Further marks do not rely on this mark being awarded.
taking the natural logarithm of both sides and attempting to transpose M1
\(\left( {{f^{ – 1}}(x)} \right) = \frac{1}{3}(\ln x – 1)\) A1
(ii) \(x \in {\mathbb{R}^ + }\) or equivalent, for example \(x > 0\). A1
[4 marks]
\(\ln x = \frac{1}{3}(\ln x – 1) \Rightarrow \ln x – \frac{1}{3}\ln x = – \frac{1}{3}\) (or equivalent) M1A1
\(\ln x = – \frac{1}{2}\) (or equivalent) A1
\(x = {{\text{e}}^{ – \frac{1}{2}}}\) A1
coordinates of \(P\) are \(\left( {{{\text{e}}^{ – \frac{1}{2}}},{\text{ }} – \frac{1}{2}} \right)\) A1
[5 marks]
coordinates of \(Q\) are (\(1,{\rm{ }}0\)) seen anywhere A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{x}\) M1
at \({\text{Q, }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1\) A1
\(y = x – 1\) AG
[3 marks]
let the required area be \(A\)
\(A = \int_1^e {x – 1{\text{d}}x – \int_1^e {\ln x{\text{d}}x} } \) M1
Note: The M1 is for a difference of integrals. Condone absence of limits here.
attempting to use integration by parts to find \(\int {\ln x{\text{d}}x} \) (M1)
\( = \left[ {\frac{{{x^2}}}{2} – x} \right]_1^{\text{e}} – [x\ln x – x]_1^{\text{e}}\) A1A1
Note: Award A1 for \(\frac{{{x^2}}}{2} – x\) and A1 for \(x\ln x – x\).
Note: The second M1 and second A1 are independent of the first M1 and the first A1.
\( = \frac{{{{\text{e}}^2}}}{2} – {\text{e}} – \frac{1}{2}\left( { = \frac{{{{\text{e}}^2} – 2{\text{e}} – 1}}{2}} \right)\) A1
[5 marks]
(i) METHOD 1
consider for example \(h(x) = x – 1 – \ln x\)
\(h(1) = 0\;\;\;{\text{and}}\;\;\;h'(x) = 1 – \frac{1}{x}\) (A1)
as \(h'(x) \ge 0\;\;\;{\text{for}}\;\;\;x \ge 1,\;\;\;{\text{then}}\;\;\;h(x) \ge 0\;\;\;{\text{for}}\;\;\;x \ge 1\) R1
as \(h'(x) \le 0\;\;\;{\text{for}}\;\;\;0 < x \le 1,\;\;\;{\text{then}}\;\;\;h(x) \ge 0\;\;\;{\text{for}}\;\;\;0 < x \le 1\) R1
so \(g(x) \le x – 1,{\text{ }}x \in {\mathbb{R}^ + }\) AG
METHOD 2
\(g”(x) = – \frac{1}{{{x^2}}}\) A1
\(g”(x) < 0\;\;\;\)(concave down) for\(\;\;\;x \in {\mathbb{R}^ + }\) R1
the graph of \(y = g(x)\) is below its tangent \((y = x – 1\;\;\;{\text{at}}\;\;\;x = 1)\) R1
so \(g(x) \le x – 1,{\text{ }}x \in {\mathbb{R}^ + }\) AG
Note: The reasoning may be supported by drawn graphical arguments.
METHOD 3
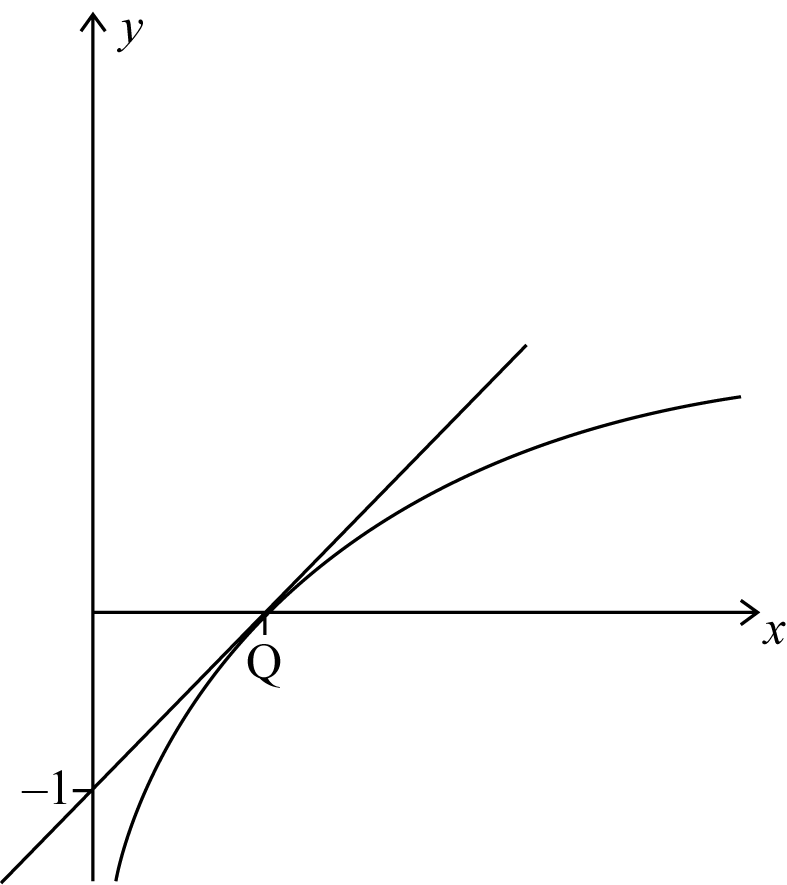
clear correct graphs of \(y = x – 1\;\;\;{\text{and}}\;\;\;\ln x\;\;\;{\text{for}}\;\;\;x > 0\) A1A1
statement to the effect that the graph of \(\ln x\) is below the graph of its tangent at \(x = 1\) R1AG
(ii) replacing \(x\) by \(\frac{1}{x}\) to obtain \(\ln \left( {\frac{1}{x}} \right) \le \frac{1}{x} – 1\left( { = \frac{{1 – x}}{x}} \right)\) M1
\( – \ln x \le \frac{1}{x} – 1\left( { = \frac{{1 – x}}{x}} \right)\) (A1)
\(\ln x \ge 1 – \frac{1}{x}\left( { = \frac{{x – 1}}{x}} \right)\) A1
so \(\frac{{x – 1}}{x} \le g(x),{\text{ }}x \in {\mathbb{R}^ + }\) AG
[6 marks]
Total [23 marks
Question
Consider the function defined by \(f(x) = {x^3} – 3{x^2} + 4\).
a.Determine the values of \(x\) for which \(f(x)\) is a decreasing function.[4]
b.There is a point of inflexion, \(P\), on the curve \(y = f(x)\).
Find the coordinates of \(P\).[3]
▶️Answer/Explanation
Markscheme
attempt to differentiate \(f(x) = {x^3} – 3{x^2} + 4\) M1
\(f'(x) = 3{x^2} – 6x\) A1
\( = 3x(x – 2)\)
(Critical values occur at) \(x = 0,{\text{ }}x = 2\) (A1)
so \(f\) decreasing on \(x \in ]0,{\text{ }}2[\;\;\;({\text{or }}0 < x < 2)\) A1
[4 marks]
\(f”(x) = 6x – 6\) (A1)
setting \(f”(x) = 0\) M1
\( \Rightarrow x = 1\)
coordinate is \((1,{\text{ }}2)\) A1
[3 marks]
Total [7 marks]
Question
Consider the function \(f\) defined by \(f(x) = {x^2} – {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
a.i.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);[2]
a.ii.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);[4]
a.iii.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).[2]
b.Find \(\int {f(x)\cos x{\text{d}}x} \).[5]
c.By finding \(g'(x)\) explain why \(g\) is an increasing function.[4]
▶️Answer/Explanation
Markscheme
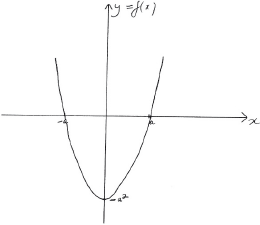
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
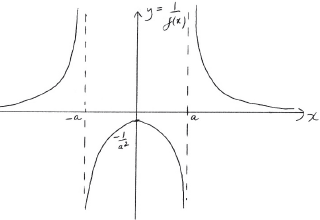
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
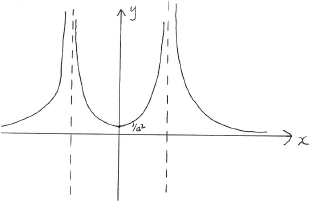
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} – {a^2})\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} – {a^2})\sin x + 2x\cos – 2\sin x + c\) A1
OR
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x – \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x – 2\sin x\)
\( – \int {{a^2}\cos x{\text{d}}x = – {a^2}\sin x} \)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x + 2x\cos x – 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} – {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} – {a^2})^{ – \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} – {a^2})^{ – \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
