Question
A curve C is given by the implicit equation \(x + y – {\text{cos}}\left( {xy} \right) = 0\).
The curve \(xy = – \frac{\pi }{2}\) intersects C at P and Q.
a.Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \left( {\frac{{1 + y\,{\text{sin}}\left( {xy} \right)}}{{1 + x\,{\text{sin}}\left( {xy} \right)}}} \right)\).[5]
b.i.Find the coordinates of P and Q.[4]
b.ii.Given that the gradients of the tangents to C at P and Q are m1 and m2 respectively, show that m1 × m2 = 1.[3]
c.Find the coordinates of the three points on C, nearest the origin, where the tangent is parallel to the line \(y = – x\).[7]
▶️Answer/Explanation
Markscheme
attempt at implicit differentiation M1
\(1 + \frac{{{\text{d}}y}}{{{\text{d}}x}} + \left( {y + x\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right){\text{sin}}\left( {xy} \right) = 0\) A1M1A1
Note: Award A1 for first two terms. Award M1 for an attempt at chain rule A1 for last term.
\(\left( {1 + x\,{\text{sin}}\left( {xy} \right)} \right)\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 1 – y\,{\text{sin}}\left( {xy} \right)\) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \left( {\frac{{1 + y\,{\text{sin}}\left( {xy} \right)}}{{1 + x\,{\text{sin}}\left( {xy} \right)}}} \right)\) AG
[5 marks]
EITHER
when \(xy = – \frac{\pi }{2},\,\,{\text{cos}}\,xy = 0\) M1
\( \Rightarrow x + y = 0\) (A1)
OR
\(x – \frac{\pi }{{2x}} – {\text{cos}}\left( {\frac{{ – \pi }}{2}} \right) = 0\) or equivalent M1
\(x – \frac{\pi }{{2x}} = 0\) (A1)
THEN
therefore \({x^2} = \frac{\pi }{2}\left( {x = \pm \sqrt {\frac{\pi }{2}} } \right)\left( {x = \pm 1.25} \right)\) A1
\({\text{P}}\left( {\sqrt {\frac{\pi }{2}} ,\, – \sqrt {\frac{\pi }{2}} } \right),\,\,{\text{Q}}\left( { – \sqrt {\frac{\pi }{2}} ,\,\sqrt {\frac{\pi }{2}} } \right)\) or \(P\left( {1.25,\, – 1.25} \right),\,Q\left( { – 1.25,\,1.25} \right)\) A1
[4 marks]
m1 = \( – \left( {\frac{{1 – \sqrt {\frac{\pi }{2}} \times – 1}}{{1 + \sqrt {\frac{\pi }{2}} \times – 1}}} \right)\) M1A1
m2 = \( – \left( {\frac{{1 + \sqrt {\frac{\pi }{2}} \times – 1}}{{1 – \sqrt {\frac{\pi }{2}} \times – 1}}} \right)\) A1
m1 m2 = 1 AG
Note: Award M1A0A0 if decimal approximations are used.
Note: No FT applies.
[3 marks]
equate derivative to −1 M1
\(\left( {y – x} \right){\text{sin}}\left( {xy} \right) = 0\) (A1)
\(y = x,\,{\text{sin}}\left( {xy} \right) = 0\) R1
in the first case, attempt to solve \(2x = {\text{cos}}\left( {{x^2}} \right)\) M1
(0.486,0.486) A1
in the second case, \({\text{sin}}\left( {xy} \right) = 0 \Rightarrow xy = 0\) and \(x + y = 1\) (M1)
(0,1), (1,0) A1
[7 marks]
Question
The following graph shows the two parts of the curve defined by the equation \({x^2}y = 5 – {y^4}\), and the normal to the curve at the point P(2 , 1).
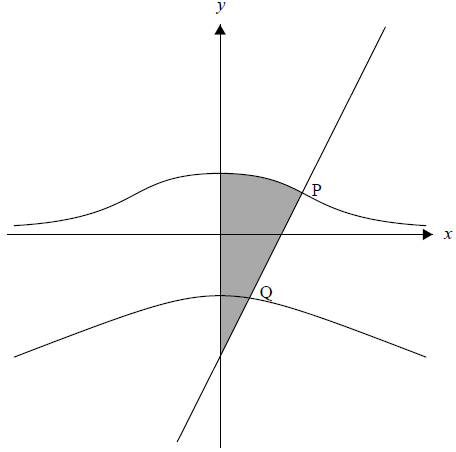
a.Show that there are exactly two points on the curve where the gradient is zero.[7]
b.Find the equation of the normal to the curve at the point P.[5]
c.The normal at P cuts the curve again at the point Q. Find the \(x\)-coordinate of Q.[3]
d.The shaded region is rotated by 2\(\pi \) about the \(y\)-axis. Find the volume of the solid formed.[7]
▶️Answer/Explanation
Markscheme
differentiating implicitly: M1
\(2xy + {x^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 4{y^3}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) A1A1
Note: Award A1 for each side.
if \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) then either \(x = 0\) or \(y = 0\) M1A1
\(x = 0 \Rightarrow \) two solutions for \(y\left( {y = \pm \sqrt[4]{5}} \right)\) R1
\(y = 0\) not possible (as 0 ≠ 5) R1
hence exactly two points AG
Note: For a solution that only refers to the graph giving two solutions at \(x = 0\) and no solutions for \(y = 0\) award R1 only.
[7 marks]
at (2, 1) \(4 + 4\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 4\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{1}{2}\) (A1)
gradient of normal is 2 M1
1 = 4 + c (M1)
equation of normal is \(y = 2x – 3\) A1
[5 marks]
substituting (M1)
\({x^2}\left( {2x – 3} \right) = 5 – {\left( {2x – 3} \right)^4}\) or \({\left( {\frac{{y + 3}}{2}} \right)^2}\,y = 5 – {y^4}\) (A1)
\(x = 0.724\) A1
[3 marks]
recognition of two volumes (M1)
volume \(1 = \pi \int_1^{\sqrt[4]{5}} {\frac{{5 – {y^4}}}{y}} {\text{d}}y\left( { = 101\pi = 3.178 \ldots } \right)\) M1A1A1
Note: Award M1 for attempt to use \(\pi \int {{x^2}} {\text{d}}y\), A1 for limits, A1 for \({\frac{{5 – {y^4}}}{y}}\) Condone omission of \(\pi \) at this stage.
volume 2
EITHER
\( = \frac{1}{3}\pi \times {2^2} \times 4\left( { = 16.75 \ldots } \right)\) (M1)(A1)
OR
\( = \pi \int_{ – 3}^1 {{{\left( {\frac{{y + 3}}{2}} \right)}^2}} {\text{d}}y\left( { = \frac{{16\pi }}{3} = 16.75 \ldots } \right)\) (M1)(A1)
THEN
total volume = 19.9 A1
[7 marks]
Question
The curve \(C\) is defined by equation \(xy – \ln y = 1,{\text{ }}y > 0\).
a.Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of \(x\) and \(y\).[4]
b.Determine the equation of the tangent to \(C\) at the point \(\left( {\frac{2}{{\text{e}}},{\text{ e}}} \right)\)[3]
▶️Answer/Explanation
Markscheme
\(y + x\frac{{{\text{d}}y}}{{{\text{d}}x}} – \frac{1}{y}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1A1A1
Note: Award A1 for the first two terms, A1 for the third term and the 0.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{y^2}}}{{1 – xy}}\) A1
Note: Accept \(\frac{{ – {y^2}}}{{\ln y}}\).
Note: Accept \(\frac{{ – y}}{{x – \frac{1}{y}}}\).
[4 marks]
\({m_T} = \frac{{{{\text{e}}^2}}}{{1 – {\text{e}} \times \frac{2}{{\text{e}}}}}\) (M1)
\({m_T} = – {{\text{e}}^2}\) (A1)
\(y – {\text{e}} = – {{\text{e}}^2}x + 2{\text{e}}\)
\( – {{\text{e}}^2}x – y + 3{\text{e}} = 0\) or equivalent A1
Note: Accept \(y = – 7.39x + 8.15\).
[3 marks]
Question
Consider the curve with equation \({x^3} + {y^3} = 4xy\).
The tangent to this curve is parallel to the \(x\)-axis at the point where \(x = k,{\text{ }}k > 0\).
a.Use implicit differentiation to show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{4y – 3{x^2}}}{{3{y^2} – 4x}}\).[3]
b.Find the value of \(k\).[5]
▶️Answer/Explanation
Markscheme
\(3{x^2} + 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4\left( {y + x\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)\) M1A1
\((3{y^2} – 4x)\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4y – 3{x^2}\) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{4y – 3{x^2}}}{{3{y^2} – 4x}}\) AG
[3 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow 4y – 3{x^2} = 0\) (M1)
substituting \(x = k\) and \(y = \frac{3}{4}{k^2}\) into \({x^3} + {y^3} = 4xy\) M1
\({k^3} + \frac{{27}}{{64}}{k^6} = 3{k^3}\) A1
attempting to solve \({k^3} + \frac{{27}}{{64}}{k^6} = 3{k^3}\) for \(k\) (M1)
\(k = 1.68{\text{ }}\left( { = \frac{4}{3}\sqrt[3]{2}} \right)\) A1
Note: Condone substituting \(y = \frac{3}{4}{x^2}\) into \({x^3} + {y^3} = 4xy\) and solving for \(x\).
[5 marks]
Examiners report
Part (a) was generally well done. Some use of partial differentiation accompanied by rudimentary partial derivative notation was observed in a few candidate’s solutions.
In part (b), a large number of candidates knew to use \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) and seemingly understood the required solution plan but were unable to correctly substitute \(x = k\) and \(y = \frac{{3{k^2}}}{4}\) into the relation and solve for \(k\).
Question
Consider the curve, \(C\) defined by the equation \({y^2} – 2xy = 5 – {{\text{e}}^x}\). The point A lies on \(C\) and has coordinates \((0,{\text{ }}a),{\text{ }}a > 0\).
a.Find the value of \(a\).[2]
b.Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\).[4]
c.Find the equation of the normal to \(C\) at the point A.[3]
d.Find the coordinates of the second point at which the normal found in part (c) intersects \(C\).[4]
e.Given that \(v = {y^3},{\text{ }}y > 0\), find \(\frac{{{\text{d}}v}}{{{\text{d}}x}}\) at \(x = 0\).[3]
▶️Answer/Explanation
Markscheme
\({a^2} = 5 – 1\) (M1)
\(a = 2\) A1
[2 marks]
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} – \left( {2x\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2y} \right) = – {{\text{e}}^x}\) M1A1A1A1
Note: Award M1 for an attempt at implicit differentiation, A1 for each part.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\) AG
[4 marks]
at \(x = 0,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{3}{4}\) (A1)
finding the negative reciprocal of a number (M1)
gradient of normal is \( – \frac{4}{3}\)
\(y = – \frac{4}{3}x + 2\) A1
[3 marks]
substituting linear expression (M1)
\({\left( { – \frac{4}{3}x + 2} \right)^2} – 2x\left( { – \frac{4}{3}x + 2} \right) + {{\text{e}}^x} – 5 = 0\) or equivalent
\(x = 1.56\) (M1)A1
\(y = – 0.0779\) A1
\((1.56,{\text{ }} – 0.0779)\)
[4 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3 \times 4 \times \frac{3}{4} = 9\) A1
[3 marks]
Question
Consider the curve, \(C\) defined by the equation \({y^2} – 2xy = 5 – {{\text{e}}^x}\). The point A lies on \(C\) and has coordinates \((0,{\text{ }}a),{\text{ }}a > 0\).
a.Find the value of \(a\).[2]
b.Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\).[4]
c.Find the equation of the normal to \(C\) at the point A.[3]
d.Find the coordinates of the second point at which the normal found in part (c) intersects \(C\).[4]
e.Given that \(v = {y^3},{\text{ }}y > 0\), find \(\frac{{{\text{d}}v}}{{{\text{d}}x}}\) at \(x = 0\).[3]
▶️Answer/Explanation
Markscheme
\({a^2} = 5 – 1\) (M1)
\(a = 2\) A1
[2 marks]
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} – \left( {2x\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2y} \right) = – {{\text{e}}^x}\) M1A1A1A1
Note: Award M1 for an attempt at implicit differentiation, A1 for each part.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\) AG
[4 marks]
at \(x = 0,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{3}{4}\) (A1)
finding the negative reciprocal of a number (M1)
gradient of normal is \( – \frac{4}{3}\)
\(y = – \frac{4}{3}x + 2\) A1
[3 marks]
substituting linear expression (M1)
\({\left( { – \frac{4}{3}x + 2} \right)^2} – 2x\left( { – \frac{4}{3}x + 2} \right) + {{\text{e}}^x} – 5 = 0\) or equivalent
\(x = 1.56\) (M1)A1
\(y = – 0.0779\) A1
\((1.56,{\text{ }} – 0.0779)\)
[4 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3 \times 4 \times \frac{3}{4} = 9\) A1
[3 marks]
Question
A particle moves in a straight line, its velocity \(v{\text{ m}}{{\text{s}}^{ – 1}}\) at time \(t\) seconds is given by \(v = 9t – 3{t^2},{\text{ }}0 \le t \le 5\).
At time \(t = 0\), the displacement \(s\) of the particle from an origin \(O\) is 3 m.
a.Find the displacement of the particle when \(t = 4\).[3]
b.Sketch a displacement/time graph for the particle, \(0 \le t \le 5\), showing clearly where the curve meets the axes and the coordinates of the points where the displacement takes greatest and least values.[5]
c.For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Given further that \(s = 16.5\) when \(t = 7.5\), find the values of \(a\) and \(b\).[3]
d.For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Find the times \({t_1}\) and \({t_2}(0 < {t_1} < {t_2} < 8)\) when the particle returns to its starting point.[4]
▶️Answer/Explanation
Markscheme
METHOD 1
\(s = \int {(9t – 3{t^2}){\text{d}}t = \frac{9}{2}{t^2} – {t^3}( + c)} \) (M1)
\(t = 0,{\text{ }}s = 3 \Rightarrow c = 3\) (A1)
\(t = 4 \Rightarrow s = 11\) A1
METHOD 2
\(s = 3 + \int_0^4 {(9t – 3{t^2}){\text{d}}t} \) (M1)(A1)
\(s = 11\) A1
[3 marks]
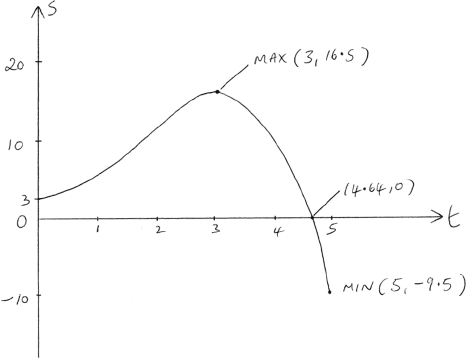
correct shape over correct domain A1
maximum at \((3,{\text{ }}16.5)\) A1
\(t\) intercept at \(4.64\), \(s\) intercept at \(3\) A1
minimum at \((5,{\text{ }} – 9.5)\) A1
[5 marks]
\( – 9.5 = a + b\cos 2\pi \)
\(16.5 = a + b\cos 3\pi \) (M1)
Note: Only award M1 if two simultaneous equations are formed over the correct domain.
\(a = \frac{7}{2}\) A1
\(b = – 13\) A1
[3 marks]
at \({t_1}\):
\(3 + \frac{9}{2}{t^2} – {t^3} = 3\) (M1)
\({t^2}\left( {\frac{9}{2} – t} \right) = 0\)
\({t_1} = \frac{9}{2}\) A1
solving \(\frac{7}{2} – 13\cos \frac{{2\pi t}}{5} = 3\) (M1)
\({\text{GDC}} \Rightarrow {t_2} = 6.22\) A1
Note: Accept graphical approaches.
[4 marks]
Total [15 marks]
