Question
The side lengths, x cm, of an equilateral triangle are increasing at a rate of 4\(cm s^{-1}\). Find the rate at which the area of the triangle, \(A {cm}^2\) is increasing when the side lengths are \(5\sqrt{3}\) cm.
\(A = \frac{1}{2} x^2 sin\frac{\pi}{2}\)
▶️Answer/Explanation
Let \( x \) be the length of a side of the equilateral triangle. Given that the side lengths are increasing at a rate of 4 cm/s, we can denote this rate of change as:
\(
\frac{dx}{dt} = 4 \, (cm\,s^{-1})
\)
To find the rate of change of the area \( A \), we start by expressing the area of an equilateral triangle as a function of its side length \( x \):
\(
A = \frac{\sqrt{3}}{4}x^2
\)
Now, we differentiate both sides of the equation with respect to \( t \) to find:
\(
\frac{dA}{dt}
\)
\(
\frac{dA}{dt} = \frac{\sqrt{3}}{4} \cdot 2x \cdot \frac{dx}{dt}
\)
Substituting the given rate of change of the side length, \( \frac{dx}{dt} = 4 \, (cm\,s^{-1}) \), and the specific side length at which we want to find the rate of change of the area, \( x = 5\sqrt{3} \, cm \), we get:
\(
\frac{dA}{dt} = \frac{\sqrt{3}}{4} \cdot 2 \cdot 5\sqrt{3} \cdot 4
\)
Simplifying, we obtain:
\(
\frac{dA}{dt} = 30 \, (cm^2\,s^{-1})
\)
Question
Consider the curve with equation \({x^2} + xy + {y^2} = 3\).
(a) Find in terms of k, the gradient of the curve at the point (−1, k).
(b) Given that the tangent to the curve is parallel to the x-axis at this point, find the value of k.
▶️Answer/Explanation
Markscheme
(a) Attempting implicit differentiation M1
\(2x + y + x\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) A1
EITHER
Substituting \(x = – 1,{\text{ }}y = k\,\,\,\,\,\)e.g. \( – 2 + k – \frac{{{\text{d}}y}}{{{\text{d}}x}} + 2k\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1
Attempting to make \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) the subject M1
OR
Attempting to make \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) the subject e.g. \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – (2x + y)}}{{x + 2y}}\) M1
Substituting \(x = – 1,{\text{ }}y = k{\text{ into }}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1
THEN
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2 – k}}{{2k – 1}}\) A1 N1
(b) Solving \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0{\text{ for }}k{\text{ gives }}k = 2\) A1
[6 marks]
Question
Consider the part of the curve \(4{x^2} + {y^2} = 4\) shown in the diagram below.
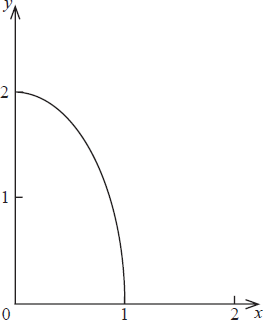
(a) Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d
}}x}}\) in terms of x and y .
(b) Find the gradient of the tangent at the point \(\left( {\frac{2}{{\sqrt 5 }},\frac{2}{{\sqrt 5 }}} \right)\).
(c) A bowl is formed by rotating this curve through \(2\pi \) radians about the x-axis.
Calculate the volume of this bowl.
▶️Answer/Explanation
Markscheme
(a) \(8x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1A1
Note: Award M1A0 for \(8x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4\) .
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{4x}}{y}\) A1
(b) – 4 A1
(c) \(V = \int {\pi {y^2}{\text{d}}x} \) or equivalent M1
\(V = \pi \int_0^1 {(4 – 4{x^2}){\text{d}}x} \) A1
\( = \pi \left[ {4x – \frac{4}{3}{x^3}} \right]_0^1\) A1
\( = \frac{{8\pi }}{3}\) A1
Note: If it is correct except for the omission of \(\pi \) , award 2 marks.
[8 marks]
Question
Show that the points (0, 0) and (\(\sqrt {2\pi } \) , \( – \sqrt {2\pi } \) ) on the curve \({{\text{e}}^{\left( {x + y} \right)}} = \cos \left( {xy} \right)\) have a common tangent.
▶️Answer/Explanation
Markscheme
attempt at implicit differentiation M1
\({{\text{e}}^{\left( {x + y} \right)}}\left( {1 + \frac{{{\text{d}}y}}{{{\text{d}}x}}} \right) = – \sin \left( {xy} \right)\left( {x\frac{{{\text{d}}y}}{{{\text{d}}x}} + y} \right)\) A1A1
let \(x = 0\), \(y = 0\) M1
\({{\text{e}}^0}\left( {1 + \frac{{{\text{d}}y}}{{{\text{d}}x}}} \right) = 0\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 1\) A1
let \(x = \sqrt {2\pi } \) , \(y = – \sqrt {2\pi } \)
\({{\text{e}}^0}\left( {1 + \frac{{{\text{d}}y}}{{{\text{d}}x}}} \right) = – \sin \left( {- 2\pi } \right)\left( {x\frac{{{\text{d}}y}}{{{\text{d}}x}} + y} \right) = 0\)
so \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 1\) A1
since both points lie on the line \(y = – x\) this is a common tangent R1
Note: \(y = – x\) must be seen for the final R1. It is not sufficient to note that the gradients are equal.
[7 marks]