IBDP Maths SL 5.7 The second derivative AA HL Paper 1- Exam Style Questions- New Syllabus
▶️ Answer/Explanation
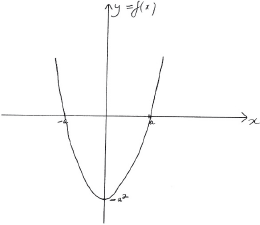
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
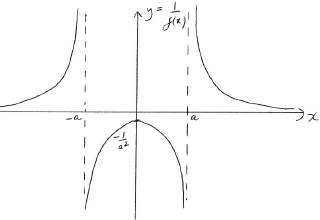
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[4 marks]
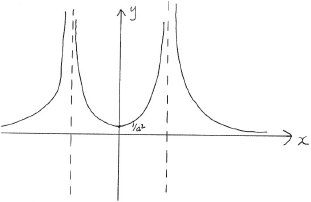
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int (x^2 – a^2)\cos x\,dx = (x^2 – a^2)\sin x – \int 2x\sin x\,dx\) A1A1
\(= (x^2 – a^2)\sin x – 2\left[ -x\cos x + \int \cos x\,dx \right]\) A1
\(= (x^2 – a^2)\sin x + 2x\cos x – 2\sin x + c\) A1
OR
\(\int (x^2 – a^2)\cos x\,dx = \int x^2\cos x\,dx – \int a^2\cos x\,dx\)
attempt at integration by parts (M1)
\(\int x^2\cos x\,dx = x^2\sin x – \int 2x\sin x\,dx\) A1A1
\(= x^2\sin x – 2\left[ -x\cos x + \int \cos x\,dx \right]\) A1
\(= x^2\sin x + 2x\cos x – 2\sin x\)
\(- \int a^2\cos x\,dx = -a^2\sin x\)
\(\int (x^2 – a^2)\cos x\,dx = (x^2 – a^2)\sin x + 2x\cos x – 2\sin x + c\) A1
[5 marks]
\(g(x) = x(x^2 – a^2)^{\frac{1}{2}}\)
\(g'(x) = (x^2 – a^2)^{\frac{1}{2}} + \frac{1}{2}x(x^2 – a^2)^{-\frac{1}{2}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = (x^2 – a^2)^{\frac{1}{2}} + x^2(x^2 – a^2)^{-\frac{1}{2}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(|x| > a\)) AG
[4 marks]
▶️ Answer/Explanation
In triangle ABC, with C at the corner, AC is in the passageway (\(\frac{3}{4}\)m wide), and BC is in the room (6m wide). Angle \(\alpha\) is between AB and the room wall.
For triangle ABC, \(\angle ACB = 90^\circ\). Using trigonometry:
\(\sec \alpha = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{AC}{\frac{3}{4}}\)
\(AC = \frac{3}{4} \sec \alpha\) A1
\(\csc \alpha = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{BC}{6}\)
\(BC = 6 \csc \alpha\) A1
Length \(L = AB = AC + BC = \frac{3}{4} \sec \alpha + 6 \csc \alpha\) A1
[3 marks]
(i) Differentiate \(L = \frac{3}{4} \sec \alpha + 6 \csc \alpha\):
\(\frac{dL}{d\alpha} = \frac{3}{4} \sec \alpha \tan \alpha – 6 \csc \alpha \cot \alpha\) M1A1
(ii) Set \(\frac{dL}{d\alpha} = 0\):
\(\frac{3}{4} \sec \alpha \tan \alpha = 6 \csc \alpha \cot \alpha\)
Multiply through by 4:
\(3 \sec \alpha \tan \alpha = 24 \csc \alpha \cot \alpha\)
Since \(\sec \alpha = \frac{1}{\cos \alpha}\), \(\tan \alpha = \frac{\sin \alpha}{\cos \alpha}\), \(\csc \alpha = \frac{1}{\sin \alpha}\), \(\cot \alpha = \frac{\cos \alpha}{\sin \alpha}\):
\(3 \cdot \frac{1}{\cos \alpha} \cdot \frac{\sin \alpha}{\cos \alpha} = 24 \cdot \frac{1}{\sin \alpha} \cdot \frac{\cos \alpha}{\sin \alpha}\)
\(\frac{3 \sin \alpha}{\cos^2 \alpha} = \frac{24 \cos \alpha}{\sin^2 \alpha}\)
Cross-multiply:
\(3 \sin^3 \alpha = 24 \cos^3 \alpha\)
\(\sin^3 \alpha = 8 \cos^3 \alpha\)
\(\left(\frac{\sin \alpha}{\cos \alpha}\right)^3 = 8\)
\(\tan^3 \alpha = 8 \implies \tan \alpha = 2 \implies \alpha = \arctan 2\) M1A1
[4 marks]
(i) Differentiate \(\frac{dL}{d\alpha} = \frac{3}{4} \sec \alpha \tan \alpha – 6 \csc \alpha \cot \alpha\):
\(\frac{d^2 L}{d\alpha^2} = \frac{3}{4} (\sec \alpha \tan^2 \alpha + \sec^3 \alpha) + 6 (\csc \alpha \cot^2 \alpha + \csc^3 \alpha)\) M1A1
(ii) At \(\alpha = \arctan 2\), \(\tan \alpha = 2\):
\(\sec^2 \alpha = 1 + \tan^2 \alpha = 1 + 4 = 5 \implies \sec \alpha = \sqrt{5}\)
\(\sin^2 \alpha = \frac{\tan^2 \alpha}{\sec^2 \alpha} = \frac{4}{5} \implies \sin \alpha = \frac{2}{\sqrt{5}}\)
\(\csc \alpha = \frac{1}{\sin \alpha} = \frac{\sqrt{5}}{2}\), \(\cot \alpha = \frac{1}{\tan \alpha} = \frac{1}{2}\)
Substitute:
\(\sec \alpha \tan^2 \alpha = \sqrt{5} \cdot 4 = 4\sqrt{5}\), \(\sec^3 \alpha = (\sqrt{5})^3 = 5\sqrt{5}\)
\(\sec \alpha \tan^2 \alpha + \sec^3 \alpha = 4\sqrt{5} + 5\sqrt{5} = 9\sqrt{5}\)
\(\frac{3}{4} (9\sqrt{5}) = \frac{27 \sqrt{5}}{4}\)
\(\csc \alpha \cot^2 \alpha = \frac{\sqrt{5}}{2} \cdot \frac{1}{4} = \frac{\sqrt{5}}{8}\), \(\csc^3 \alpha = \left(\frac{\sqrt{5}}{2}\right)^3 = \frac{5\sqrt{5}}{8}\)
\(\csc \alpha \cot^2 \alpha + \csc^3 \alpha = \frac{\sqrt{5}}{8} + \frac{5\sqrt{5}}{8} = \frac{6\sqrt{5}}{8} = \frac{3\sqrt{5}}{4}\)
\(6 \left(\frac{3\sqrt{5}}{4}\right) = \frac{18\sqrt{5}}{4} = \frac{9\sqrt{5}}{2}\)
\(\frac{d^2 L}{d\alpha^2} = \frac{27 \sqrt{5}}{4} + \frac{9\sqrt{5}}{2} = \frac{27 \sqrt{5} + 18 \sqrt{5}}{4} = \frac{45 \sqrt{5}}{4}\) M1A1
[4 marks]
(i) At \(\alpha = \arctan 2\), \(\frac{dL}{d\alpha} = 0\) and \(\frac{d^2 L}{d\alpha^2} = \frac{45}{4} \sqrt{5} > 0\) (concave up), indicating a minimum. A1
(ii) Compute \(L = \frac{3}{4} \sec \alpha + 6 \csc \alpha\) at \(\alpha = \arctan 2\):
\(\tan \alpha = 2\), \(\sec \alpha = \sqrt{5}\), \(\csc \alpha = \frac{\sqrt{5}}{2}\)
\(L = \frac{3}{4} \sqrt{5} + 6 \cdot \frac{\sqrt{5}}{2} = \frac{3 \sqrt{5}}{4} + 3 \sqrt{5} = \frac{3 \sqrt{5} + 12 \sqrt{5}}{4} = \frac{15 \sqrt{5}}{4}\) M1A1
[3 marks]
Minimum length \(L = \frac{15 \sqrt{5}}{4} \approx 8.385 \, \text{m}\).
Pole length = 11.25 m, which is greater than \(\frac{15 \sqrt{5}}{4}\).
Since the minimum possible length \(L\) is less than 11.25 m, the pole cannot be carried horizontally through the corner without exceeding the geometric constraints. R1A1
[2 marks]