Question
Let y = \(\frac{Inx}{x^{4}}\) for x > 0.
(a) Show that \(\frac{dy}{dx}= \frac{1-4Inx}{x^{5}}\)
Consider the function defined by f (x) \(\frac{Inx}{x^{4}}\) = for x> 0 and its graph y = f (x) .
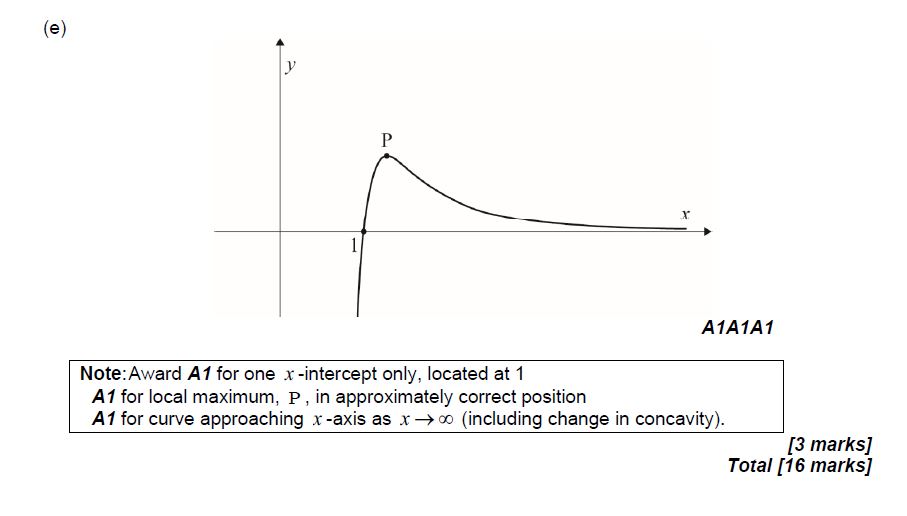
(b) The graph of f has a horizontal tangent at point P. Find the coordinates of P. [5]
(c) Given that f ” (x) = \(\frac{20Lnx-9}{x^{6}}\) show that P is a local maximum point. [3]
(d) Solve f (x) > 0 for x > 0. [2]
(e) Sketch the graph of f , showing clearly the value of the x-intercept and the approximate position of point P. [3]
Answer/Explanation
Ans



Question
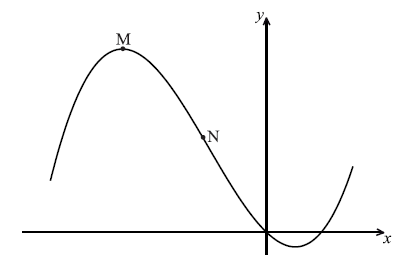
Consider \(f(x) = \frac{1}{3}{x^3} + 2{x^2} – 5x\) . Part of the graph of f is shown below. There is a maximum point at M, and a point of inflexion at N.
Find \(f'(x)\) .[3]
Find the x-coordinate of M.[4]
Find the x-coordinate of N.[3]
The line L is the tangent to the curve of f at \((3{\text{, }}12)\). Find the equation of L in the form \(y = ax + b\) .[4]
Answer/Explanation
Markscheme
\(f'(x) = {x^2} + 4x – 5\) A1A1A1 N3
[3 marks]
evidence of attempting to solve \(f'(x) = 0\) (M1)
evidence of correct working A1
e.g. \((x + 5)(x – 1)\) , \(\frac{{ – 4 \pm \sqrt {16 + 20} }}{2}\) , sketch
\(x = – 5\), \(x = 1\) (A1)
so \(x = – 5\) A1 N2
[4 marks]
METHOD 1
\(f”(x) = 2x + 4\) (may be seen later) A1
evidence of setting second derivative = 0 (M1)
e.g. \(2x + 4 = 0\)
\(x = – 2\) A1 N2
METHOD 2
evidence of use of symmetry (M1)
e.g. midpoint of max/min, reference to shape of cubic
correct calculation A1
e.g. \(\frac{{ – 5 + 1}}{2}\)
\(x = – 2\) A1 N2
[3 marks]
attempting to find the value of the derivative when \(x = 3\) (M1)
\(f'(3) = 16\) A1
valid approach to finding the equation of a line M1
e.g. \(y – 12 = 16(x – 3)\) , \(12 = 16 \times 3 + b\)
\(y = 16x – 36\) A1 N2
[4 marks]
Question
Let \(f(x) = 3 + \frac{{20}}{{{x^2} – 4}}\) , for \(x \ne \pm 2\) . The graph of f is given below.
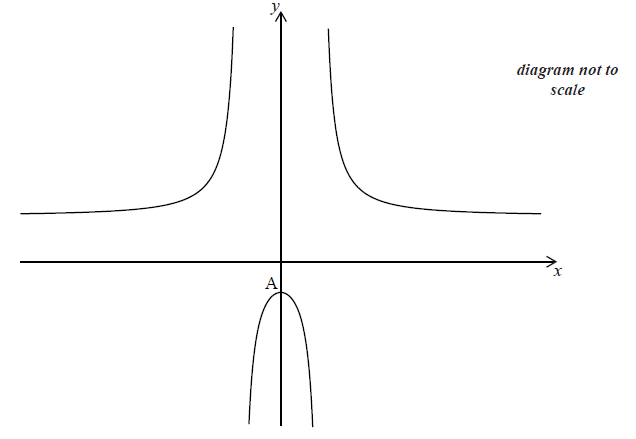
The y-intercept is at the point A.
(i) Find the coordinates of A.
(ii) Show that \(f'(x) = 0\) at A.[7]
The second derivative \(f”(x) = \frac{{40(3{x^2} + 4)}}{{{{({x^2} – 4)}^3}}}\) . Use this to
(i) justify that the graph of f has a local maximum at A;
(ii) explain why the graph of f does not have a point of inflexion.[6]
Describe the behaviour of the graph of \(f\) for large \(|x|\) .[1]
Write down the range of \(f\) .[2]
Answer/Explanation
Markscheme
(i) coordinates of A are \((0{\text{, }} – 2)\) A1A1 N2
(ii) derivative of \({x^2} – 4 = 2x\) (seen anywhere) (A1)
evidence of correct approach (M1)
e.g. quotient rule, chain rule
finding \(f'(x)\) A2
e.g. \(f'(x) = 20 \times ( – 1) \times {({x^2} – 4)^{ – 2}} \times (2x)\) , \(\frac{{({x^2} – 4)(0) – (20)(2x)}}{{{{({x^2} – 4)}^2}}}\)
substituting \(x = 0\) into \(f'(x)\) (do not accept solving \(f'(x) = 0\) ) M1
at A \(f'(x) = 0\) AG N0
[7 marks]
(i) reference to \(f'(x) = 0\) (seen anywhere) (R1)
reference to \(f”(0)\) is negative (seen anywhere) R1
evidence of substituting \(x = 0\) into \(f”(x)\) M1
finding \(f”(0) = \frac{{40 \times 4}}{{{{( – 4)}^3}}}\) \(\left( { = – \frac{5}{2}} \right)\) A1
then the graph must have a local maximum AG
(ii) reference to \(f”(x) = 0\) at point of inflexion (R1)
recognizing that the second derivative is never 0 A1 N2
e.g. \(40(3{x^2} + 4) \ne 0\) , \(3{x^2} + 4 \ne 0\) , \({x^2} \ne – \frac{4}{3}\) , the numerator is always positive
Note: Do not accept the use of the first derivative in part (b).
[6 marks]
correct (informal) statement, including reference to approaching \(y = 3\) A1 N1
e.g. getting closer to the line \(y = 3\) , horizontal asymptote at \(y = 3\)
[1 mark]
correct inequalities, \(y \le – 2\) , \(y > 3\) , FT from (a)(i) and (c) A1A1 N2
[2 marks]
Question
Let \(f(x) = \frac{1}{2}{x^3} – {x^2} – 3x\) . Part of the graph of f is shown below.
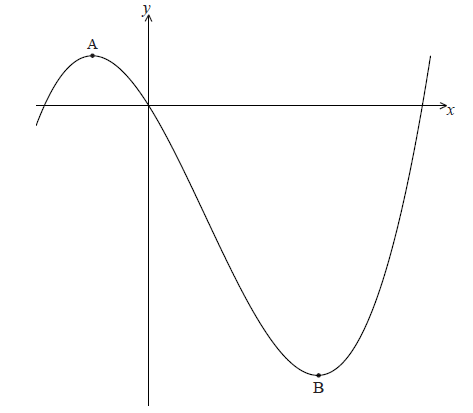
There is a maximum point at A and a minimum point at B(3, − 9) .
Find the coordinates of A.[8]
Write down the coordinates of
(i) the image of B after reflection in the y-axis;
(ii) the image of B after translation by the vector \(\left( {\begin{array}{*{20}{c}}
{ – 2}\\
5
\end{array}} \right)\) ;
(iii) the image of B after reflection in the x-axis followed by a horizontal stretch with scale factor \(\frac{1}{2}\) .[6]
Answer/Explanation
Markscheme
\(f(x) = {x^2} – 2x – 3\) A1A1A1
evidence of solving \(f'(x) = 0\) (M1)
e.g. \({x^2} – 2x – 3 = 0\)
evidence of correct working A1
e.g. \((x + 1)(x – 3)\) , \(\frac{{2 \pm \sqrt {16} }}{2}\)
\(x = – 1\) (ignore \(x = 3\) ) (A1)
evidence of substituting their negative x-value into \(f(x)\) (M1)
e.g. \(\frac{1}{3}{( – 1)^3} – {( – 1)^2} – 3( – 1)\) , \( – \frac{1}{3} – 1 + 3\)
\(y = \frac{5}{3}\) A1
coordinates are \(\left( { – 1,\frac{5}{3}} \right)\) N3
[8 marks]
(i) \(( – 3{\text{, }} – 9)\) A1 N1
(ii) \((1{\text{, }} – 4)\) A1A1 N2
(iii) reflection gives \((3{\text{, }}9)\) (A1)
stretch gives \(\left( {\frac{3}{2}{\text{, }}9} \right)\) A1A1 N3
[6 marks]
Question
[without GDC]
Given the following values at \(x =1\)
![]()
Calculate the derivatives of the following functions at \(x =1\)
(ⅰ) \(y=2f(x)+3g(x)\) (ⅰⅰ) \(y=f(x)g(x)\)
(ⅰⅰⅰ) \(y=\frac{f(x)}{g(x)}\) (iv) \(y=2x^{3}+1+5f(x)\)
Answer/Explanation
Ans
(a) \(\frac{\mathrm{d} y}{\mathrm{d} x}=2f'(x)+3g'(x)\), at \(x=1\) the value is \(23\)
(b) \(\frac{\mathrm{d} y}{\mathrm{d} x}=f'(x)g(x)+f(x)g'(x)\), at \(x=1\) the value is \(22\)
(c) \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^{2}}\), at \(x=1\) the value is \(\frac{2}{9}\)
(d) \(\frac{\mathrm{d} y}{\mathrm{d} x}=6x^{2}+5f'(x)\), at \(x=1\) the value is \(26\)
