IBDP Maths AHL 5.14 Implicit differentiation AA HL Paper 2- Exam Style Questions- New Syllabus

(a) Method 1
Differentiate implicitly: \( \frac{d}{dx}(4x^2) + \frac{d}{dx}(y^2) – \frac{d}{dx}(24x) + \frac{d}{dx}(4y) + \frac{d}{dx}(20) = 0 \)
\( 8x + 2y\frac{dy}{dx} – 24 + 4\frac{dy}{dx} = 0 \)
Factor \( \frac{dy}{dx} \): \( (2y + 4)\frac{dy}{dx} = 24 – 8x \)
\( \frac{dy}{dx} = \frac{24 – 8x}{2y + 4} = \frac{4(3 – x)}{y + 2} \) ✓

(b)
Domain occurs where derivative is undefined: \( y + 2 = 0 \) ⇒ \( y = -2 \)
Substitute \( y = -2 \) into curve equation: \( 4x^2 + (-2)^2 – 24x + 4(-2) + 20 = 0 \)
\( 4x^2 + 4 – 24x – 8 + 20 = 0 \) ⇒ \( 4x^2 – 24x + 16 = 0 \)
Divide by 4: \( x^2 – 6x + 4 = 0 \)
Solve: \( x = \frac{6 \pm \sqrt{36 – 16}}{2} = \frac{6 \pm \sqrt{20}}{2} = 3 \pm \sqrt{5} \)
Domain: \( \boxed{3 – \sqrt{5} \leq x \leq 3 + \sqrt{5}} \) (so \( a = 5 \))

(c)
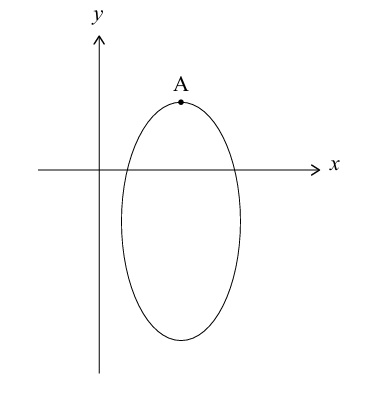
At maximum point \( A \), \( \frac{dy}{dx} = 0 \) ⇒ \( 4(3 – x) = 0 \) ⇒ \( x = 3 \)
Substitute \( x = 3 \) into curve: \( 4(3)^2 + y^2 – 24(3) + 4y + 20 = 0 \)
\( 36 + y^2 – 72 + 4y + 20 = 0 \) ⇒ \( y^2 + 4y – 16 = 0 \)
Solve: \( y = \frac{-4 \pm \sqrt{16 + 64}}{2} = \frac{-4 \pm \sqrt{80}}{2} = \frac{-4 \pm 4\sqrt{5}}{2} = -2 \pm 2\sqrt{5} \)
Maximum point ⇒ take positive: \( y = -2 + 2\sqrt{5} \approx 2.472 \)
\( \boxed{A(3, -2 + 2\sqrt{5})} \) or \( \boxed{A(3, 2.47)} \)

(d)
Substitute \( y = mx \) into curve: \( 4x^2 + (mx)^2 – 24x + 4(mx) + 20 = 0 \)
\( (4 + m^2)x^2 + (4m – 24)x + 20 = 0 \)
For tangency, discriminant \( \Delta = 0 \):
\( (4m – 24)^2 – 4(4 + m^2)(20) = 0 \)
\( 16m^2 – 192m + 576 – 320 – 80m^2 = 0 \)
\( -64m^2 – 192m + 256 = 0 \) ⇒ Divide by -64: \( m^2 + 3m – 4 = 0 \)
\( (m + 4)(m – 1) = 0 \) ⇒ \( m = -4 \) or \( m = 1 \)
\( \boxed{m = -4, 1} \)

(e)
Method 1: Substitute \( x = -\frac{1}{4}y \) (since \( y = -4x \)) into curve:
\( 4(-\frac{1}{4}y)^2 + y^2 – 24(-\frac{1}{4}y) + 4y + 20 = 0 \)
\( 4(\frac{1}{16}y^2) + y^2 + 6y + 4y + 20 = 0 \)
\( \frac{1}{4}y^2 + y^2 + 10y + 20 = 0 \) ⇒ \( \frac{5}{4}y^2 + 10y + 20 = 0 \)
Multiply by 4: \( 5y^2 + 40y + 80 = 0 \) ⇒ Divide by 5: \( y^2 + 8y + 16 = 0 \)
\( (y + 4)^2 = 0 \) ⇒ \( y = -4 \)
\( \boxed{y_B = -4} \)

(f)
Solve curve equation for \( x \) in terms of \( y \): \( 4x^2 – 24x + (y^2 + 4y + 20) = 0 \)
Quadratic formula: \( x = \frac{24 \pm \sqrt{(-24)^2 – 4(4)(y^2 + 4y + 20)}}{2(4)} \)
\( x = \frac{24 \pm \sqrt{576 – 16(y^2 + 4y + 20)}}{8} = \frac{24 \pm \sqrt{256 – 16y^2 – 64y}}{8} \)
Simplify: \( x = \frac{24 \pm 4\sqrt{16 – y^2 – 4y}}{8} = 3 \pm \frac{1}{2}\sqrt{16 – 4y – y^2} \)
Right branch: \( x = 3 – \frac{1}{2}\sqrt{16 – 4y – y^2} \) (since curve is to left of max)
Volume: \( V = \pi \int_{-4}^{-2 + 2\sqrt{5}} \left( 3 – \frac{1}{2}\sqrt{16 – 4y – y^2} \right)^2 dy \)
Numerical integration: \( V \approx 29.708 \)
\( \boxed{29.7} \)