Question: [Maximum mark: 7]
A particle moves along a straight line so that its velocity, vms-1, after t seconds is given by v(t) = esint + 4sint for 0 ≤ t ≤ 6.
(a) Find the value of t when the particle is at rest.
(b) Find the acceleration of the particle when it changes direction.
(c) Find the total distance travelled by the particle.
▶️Answer/Explanation
Ans:
(a) recognizing at rest v = 0
t = 3.34692…
t = 3.35 (seconds)
Note: Award (M1)A0 for any other solution to v = 0 eg t = −0.205 or t = 6.08.
(b) recognizing particle changes direction when v = 0 OR when t = 3.34692…
a = −4.71439…
a = −4.71(ms-2 )
(c) distance travelled = \(\int_{0}^{6}|v|dt\) OR
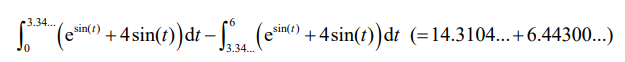
= 20.7534…
= 20.8 (metres)
Question
The acceleration, a ms-2 , of a particle moving in a horizontal line at time t seconds, t ≥ 0 , is given by a = – (1+v) where v ms-1 is the particle’s velocity and v > -1.
At t = 0 , the particle is at a fixed origin O and has initial velocity v0 ms-1 .
(a) By solving an appropriate differential equation, show that the particle’s velocity at time t is given by v ( t ) = (1 + v0) e-t – 1 . [6]
(b) Initially at O, the particle moves in the positive direction until it reaches its maximum displacement from O. The particle then returns to O.
Let s metres represent the particle’s displacement from O and smax its maximum displacement from O.
(i) Show that the time T taken for the particle to reach smax satisfies the equation eT = 1 + v0 .
(ii) By solving an appropriate differential equation and using the result from part (b) (i), find an expression for smax in terms of v0 . [7]
Let v (T – k) represent the particle’s velocity k seconds before it reaches smax , where v (T – k) = (1 + v0) e-(T – k) – 1 .
(c) By using the result to part (b) (i), show that v (T – k) = ek – 1 . [2]
Similarly, let v (T + k) represent the particle’s velocity k seconds after it reaches smax .
(d) Deduce a similar expression for v (T + k) in terms of k . [2]
(e) Hence, show that v (T – k) + v (T + k) ≥ 0 . [3]
▶️Answer/Explanation
Ans:
(a) Since $a=\frac{\text{d}v}{\text{d}t}$, and $a=-\left(1+v\right)$, we have
$$\begin{eqnarray}
\frac{\text{d}v}{\text{d}t} = -1-v \nonumber \\
\frac{\text{d}v}{\text{d}t}+v = -1.
\end{eqnarray}$$
Let $\text{I}\left(x\right)=\text{e}^{\int 1 \text{d}t}=\text{e}^t$.<br>
Then, we have
$$\begin{eqnarray}
\frac{\text{d}}{\text{d}t}\left(v\text{e}^t\right) = -\text{e}^t \nonumber \\
v\text{e}^t = -\int\text{e}^t \text{d}t \nonumber \\
v\text{e}^t = -\text{e}^t+c \nonumber \\
v = c\text{e}^{-t}-1.
\end{eqnarray}$$
Since $v=v_0$ when $t=0$, we have $c=1+v_0$, i.e., $v=\left(1+v_0\right)\text{e}^{-t}-1$.<br>
(b)(i) At $s_{\text{max}}$, $t=T$, i.e., we have
$$\begin{eqnarray}
v\left(T\right) = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T}-1 = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T} = 1 \nonumber \\
1+v_0 = \text{e}^T.
\end{eqnarray}$$
(b)(ii) Since $\frac{\text{d}s}{\text{d}t}=\left(1+v_0\right)\text{e}^{-t}-1$, integrating both sides with respect to $t$, we have
$$\begin{eqnarray}
s &=& \int\left(1+v_0\right)\text{e}^{-t}-1\text{d}t \nonumber \\
&=& -\left(1+v_0\right)\text{e}^{-t}-t+c.
\end{eqnarray}$$
When $t=0$, $s=0$, i.e.,
$$\begin{eqnarray}
0 = -\left(1+v_0\right)+c \nonumber \\
c = \left(1+v_0\right).
\end{eqnarray}$$
Thus, $s=\left(1+v_0\right)-\left(1+v_0\right)\text{e}^{-t}-t$.<br>
Since from (b)(i) we have $1+v_0=\text{e}^T$, $T=\ln\left(1+v_0\right)$, i.e., $s_{\text{max}}=v_0-\ln \left(1+v_0\right)$.<br>
(c) Since $\text{e}^T=1+v_0$, we have $\left(1+v_0\right)\text{e}^{-T}=1$, i.e.,
$$\begin{eqnarray}
v\left(T-k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T-k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^k-1 \nonumber \\
&=& \text{e}^k-1.
\end{eqnarray}$$
(d) Similarly, as in (c),
$$\begin{eqnarray}
v\left(T+k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T+k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^{-k}-1.
\end{eqnarray}$$
(e)
$$\begin{eqnarray}
v\left(T-k\right)+v\left(T+k\right) &=& \text{e}^k-1+\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^k+\text{e}^{-k}-2 \nonumber \\
&=& \frac{\text{e}^{2k}-2\text{e}^k+1}{\text{e}^k} \nonumber \\
&=& \frac{\left(\text{e}^k-1\right)^2}{\text{e}^k} \geq 0.
\end{eqnarray}$$
Question
A particle P moves in a straight line with displacement relative to origin given by
\[s = 2\sin (\pi t) + \sin (2\pi t),{\text{ }}t \geqslant 0,\]
where t is the time in seconds and the displacement is measured in centimetres.
(i) Write down the period of the function s.
(ii) Find expressions for the velocity, v, and the acceleration, a, of P.
(iii) Determine all the solutions of the equation v = 0 for \(0 \leqslant t \leqslant 4\).
Consider the function
\[f(x) = A\sin (ax) + B\sin (bx),{\text{ }}A,{\text{ }}a,{\text{ }}B,{\text{ }}b,{\text{ }}x \in \mathbb{R}.\]
Use mathematical induction to prove that the\({(2n)^{{\text{th}}}}\) derivative of f is given by \(({f^{(2n)}}(x) = {( – 1)^n}\left( {A{a^{2n}}\sin (ax) + B{b^{2n}}\sin (bx)} \right)\), for all \(n \in {\mathbb{Z}^ + }\).
▶️Answer/Explanation
Markscheme
(i) the period is 2 A1
(ii) \(v = \frac{{{\text{d}}s}}{{{\text{d}}t}} = 2\pi \cos (\pi t) + 2\pi \cos (2\pi t)\) (M1)A1
\(a = \frac{{{\text{d}}v}}{{{\text{d}}t}} = – 2{\pi ^2}\sin (\pi t) – 4{\pi ^2}\sin (2\pi t)\) (M1)A1
(iii) \(v = 0\)
\(2\pi \left( {\cos (\pi t) + \cos (2\pi t)} \right) = 0\)
EITHER
\(\cos (\pi t) + 2{\cos ^2}(\pi t) – 1 = 0\) M1
\(\left( {2\cos (\pi t) – 1} \right)\left( {\cos (\pi t) + 1} \right) = 0\) (A1)
\(\cos (\pi t) = \frac{1}{2}{\text{ or }}\cos (\pi t) = – 1\) A1
\(t = \frac{1}{3},{\text{ }}t = 1\) A1
\(t = \frac{5}{3},{\text{ }}t = \frac{7}{3},{\text{ }}t = \frac{{11}}{3},{\text{ }}t = 3\) A1
OR
\(2\cos \left( {\frac{{\pi t}}{2}} \right)\cos \left( {\frac{{3\pi t}}{2}} \right) = 0\) M1
\(\cos \left( {\frac{{\pi t}}{2}} \right) = 0{\text{ or }}\cos \left( {\frac{{3\pi t}}{2}} \right) = 0\) A1A1
\(t = \frac{1}{3},{\text{ 1}}\) A1
\(t = \frac{5}{3},{\text{ }}\frac{7}{3},{\text{ }}3,{\text{ }}\frac{{11}}{3}\) A1
[10 marks]
\(P(n):{f^{(2n)}}(x) = {( – 1)^n}\left( {A{a^{2n}}\sin (ax) + B{b^{2n}}\sin (bx)} \right)\)
\(P(1):f”(x) = {\left( {Aa\cos (ax) + Bb\cos (bx)} \right)^\prime }\) M1
\( = – A{a^2}\sin (ax) – B{b^2}\sin (bx)\)
\( = – 1\left( {A{a^2}\sin (ax) + B{b^2}\sin (bx)} \right)\) A1
\(\therefore P(1)\) true
assume that
\(P(k):{f^{(2k)}}(x) = {( – 1)^k}\left( {A{a^{2k}}\sin (ax) + B{b^{2k}}\sin (bx)} \right)\) is true M1
consider \(P(k + 1)\)
\({f^{(2k + 1)}}(x) = {( – 1)^k}\left( {A{a^{2k + 1}}\cos (ax) + B{b^{2k + 1}}\cos (bx)} \right)\) M1A1
\({f^{(2k + 2)}}(x) = {( – 1)^k}\left( { – A{a^{2k + 2}}\sin (ax) – B{b^{2k + 2}}\sin (bx)} \right)\) A1
\( = {( – 1)^{k + 1}}\left( {A{a^{2k + 2}}\sin (ax) + B{b^{2k + 2}}\sin (bx)} \right)\) A1
\(P(k)\) true implies \(P(k + 1)\) true, \(P(1)\) true so \(P(n)\) true \(\forall n \in {\mathbb{Z}^ + }\) R1
Note: Award the final R1 only if the previous three M marks have been awarded.
[8 marks]
Examiners report
In (a), only a few candidates gave the correct period but the expressions for velocity and acceleration were correctly obtained by most candidates. In (a)(iii), many candidates manipulated the equation v = 0 correctly to give the two possible values for \(\cos (\pi t)\) but then failed to find all the possible values of t.
Solutions to (b) were disappointing in general with few candidates giving a correct solution.
Question
A body is moving in a straight line. When it is \(s\) metres from a fixed point O on the line its velocity, \(v\), is given by \(v = – \frac{1}{{{s^2}}},{\text{ }}s > 0\).
Find the acceleration of the body when it is 50 cm from O.
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = 2{s^{ – 3}}\) M1A1
Note: Award M1 for \(2{s^{ – 3}}\) and A1 for the whole expression.
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\) (M1)
\(a = – \frac{1}{{{s^2}}} \times \frac{2}{{{s^3}}}\left( { = – \frac{2}{{{s^5}}}} \right)\) (A1)
when \(s = \frac{1}{2},{\text{ }}a = – \frac{2}{{{{(0.5)}^5}}}{\text{ }}( = – 64){\text{ (m}}{{\text{s}}^{ – 2}})\) M1A1
Note: M1 is for the substitution of 0.5 into their equation for acceleration.
Award M1A0 if \(s = 50\) is substituted into the correct equation.
[6 marks]
Examiners report
Question
A particle moves in a straight line such that at time \(t\) seconds \((t \geqslant 0)\), its velocity \(v\), in \({\text{m}}{{\text{s}}^{ – 1}}\), is given by \(v = 10t{{\text{e}}^{ – 2t}}\). Find the exact distance travelled by the particle in the first half-second.
▶️Answer/Explanation
Markscheme
\(s = \int\limits_0^{\frac{1}{2}} {10t{{\text{e}}^{ – 2t}}{\text{d}}t} \)
attempt at integration by parts M1
\( = \left[ { – 5t{{\text{e}}^{ – 2t}}} \right]_0^{\frac{1}{2}} – \int\limits_0^{\frac{1}{2}} { – 5{{\text{e}}^{ – 2t}}{\text{d}}t} \) A1
\( = \left[ { – 5t{{\text{e}}^{ – 2t}} – \frac{5}{2}{{\text{e}}^{ – 2t}}} \right]_0^{\frac{1}{2}}\) (A1)
Note: Condone absence of limits (or incorrect limits) and missing factor of 10 up to this point.
\(s = \int\limits_0^{\frac{1}{2}} {10t{{\text{e}}^{ – 2t}}{\text{d}}t} \) (M1)
\( = – 5{{\text{e}}^{ – 1}} + \frac{5}{2}{\text{ }}\left( { = \frac{{ – 5}}{{\text{e}}} + \frac{5}{2}} \right){\text{ }}\left( { = \frac{{5{\text{e}} – 10}}{{2{\text{e}}}}} \right)\) A1
[5 marks]
Examiners report
A. Practice Questions
Question
The displacement s of an oscillating body from a fixed point \(O\) in a straight line, is given by \(s=\sin (\frac{t}{4}),t \ge 0\)
- Find expressions for the velocity and the acceleration in terms of time \(t\).
- Find the maximum displacement.
- Find the times it passes the fixed point \(O\).
- Find the two values of the velocity at these times (found in (\(c\)))
- Find the times when the body changes direction.
- Find the two values of the acceleration at these times (found in (\(e\)))
▶️Answer/Explanation
Ans:
- \(v=\frac{1}{4}\cos (\frac{t}{4})\)
- \(a=-\frac{1}{16}\sin (\frac{t}{4})\)
- \(s_{max}=1\)
\(s=0\) at \(t=0,4\pi,8\pi,… (i.e.\space t=4k\pi,k \in Z^{+})\) - \(\pm \frac{1}{4}ms^{-1}\)
- \(v=0\) at \(t=2\pi,6\pi,10\pi,… (i.e.\space t=2\pi+4k\pi,k \in Z^{+})\)
- \(\pm \frac{1}{16}ms^{-2}\)
Question
The velocity \(v\) of a car, \(t\) seconds after leaving a fixed point \(A\), is given by
\(v=16-4e^{2t}\)
- Calculate the acceleration of the car after \(\ln 3\) seconds.
- Calculate the displacement of the car in terms of \(t\), given that the initial displacement is 0.
- The car is stationary at time \(t\). Find the exact value of \(t\).
- Find the displacement and the distance travelled after \(\ln 4\) seconds.
- \(a=-8e^{2t},\)
At \(t= \ln 3 \space a=-8e^{2 \ln 3}=-72 ms^{-2}\) - \(s=\int 16-4e^{2t}dt=16t-2e^{2t}+c\)
\(s(0)=0\)⇒\(c=2\)
\(s=16t-2e^{2t}+2\) - \(v=0\)⇔\(16-4e^{2t}=0\)⇔\(t=\ln 2\)
- \(s=32 \ln 2 -30m,\)
distance travelled = \(\int_{0}^{\ln 3}|16-4e^{2t}|dt\)
=\(\int_{0}^{\ln 2}(16-4e^{2t})dt-\int_{\ln 2}^{\ln 3}(16-4e^{2t}dt\)
=\(18m\)
Question
Particle \(A\) moves in a straight line, starting from \(O_A\), such that its velocity in metres per second for \(0 \le t \le 9\) is given by
\(v_A=-\frac{1}{2}t^2+3t+\frac{3}{2}\).
Particle B moves in a straight line, starting from \(O_B\), such that its velocity in metres per second for \(0 \le t \le 9\) is given by
\(v_B=e^{0.2t}\).
(a) Find the maximum value of \(v_A\), justifying that it is a maximum.
(b) Find the acceleration of \(B\) when \(t=4\).
The displacements of \(A\) and \(B\) from \(O_A\), and \(O_B\) respectively, at time \(t\) are \(s_A\), metres and \(s_B\) metres. When \(t=0, s_A= 0,\) and \(s_B= 5\).
(c) Find an expression for \(s_A\) and for \(s_B\), giving your answers in terms of \(t\).
(d) (i) Sketch the curves of \(s_A\) and \(s_B\) on the same diagram.
(ii) Find the values of \(t\) at which \(s_A\)=\(s_B\).
▶️Answer/Explanation
Ans:
A particle moves in a straight line with velocity, in metres per sec, at time \(t\) seconds, given by \(v(t) = 6t^2 – 6t, t ≥ 0\)Calculate the total distance travelled by the particle in the first two seconds of motion.Extra question: If the initial displacement is \(0m\), find the displacement after two seconds.(Compare with the distance travelled found above)
Question
- A particle moves along a straight line and its velocity at time \(t\) is given by \(v = 10t.\)
Find its acceleration. - A particle moves along a straight line. When it is in distance \(s\) from a fixed point, the velocity \(v\) is given by \(v = 10s\). Find the acceleration in terms of \(s\).
▶️Answer/Explanation
Ans:
\(a = 10 ms^{-2}\)
\(a = 100s\)
Question
Find the acceleration if
- \(v = t^2 + 10e^t \)
- \(v = s^2 + 10e^s\)
▶️Answer/Explanation
Ans:
\(a=2t+10e^t\)
\(a=(2s+10e^s)v=(2s+10e^s)(s^2+10e^s)\)
Question
The displacement \(s\) metres of a moving body \(B\) from a fixed point \(O\) at time \(t\) seconds is given by
\(s = 50t – 10t^2 + 1000.\)
- Find the velocity of \(B\) in \(m s^{–1}\).
- Find its maximum displacement from \(O\).
Extra question: Find the acceleration in \(m s^{–2}\).
▶️Answer/Explanation
Ans:
- \(s = 50t = 10t^2 + 1000\)
\(v=\frac{ds}{dt}=50-20t\) - Displacement is max when \(v=0,\)
i.e. when \(t=\frac{5}{2}\).
Substituting \(t=\frac{5}{2}, s=50×\frac{5}{2}-10×(\frac{5}{2})^2+1000\)
\(s=1062.5 m\)
Extra question: \(a=-20 ms^{-2}\)
Question
An astronaut on the moon throws a ball vertically upwards. The height, \(s\) metres, of the ball, after \(t\) seconds, is given by the equation \(s = 40t + 0.5at^2\), where \(a\) is a constant. If the ball reaches its maximum height when \(t = 25,\) find the value of \(a\)
▶️Answer/Explanation
Given \(s = 40t + 0.5at^2,\) then the maximum height is reached when \(\frac{ds}{dt}=0\)
\(at+40=0\)
\(a=-\frac{40}{25}=-1.6\)(units not required)
Extra question: acceleration = \(\frac{d^2s}{dt^2}=a \space ms^{-2}\)
Question
A particle moves in a straight line. At time \(t\) seconds, its displacement from a fixed point \(O\) is \(s\) metres, and its velocity, \(v\) metres per second, is given by \(v=3t^2-4t+2, t \ge 0.\)
When \(t = 0 , s = −3\). Find the value of \(t\) when the particle is at \(O\).
▶️Answer/Explanation
Ans:
METHOD 1
\(s= \int (3t^2-4t+2)dt\)
Attempting to integrate the \(RHS\)
\(s=t^3-2t^2+2t+C\)
Using \(s(0)=-3\) gives \(C=-3 \space (s=t^3-2t^2+2t-3\)
Solving \(t^3-2t^2+2t-3=0\) for \(t\)
\(t=1.81 (sec)\)
METHOD 2
\(\int_{0}^{T}(3t^2-4t+2)dt=\int_{-3}^{0} ds (=3)\)
Solving for \(T\)
\(T=1.81 (sec)\)
Question
The acceleration, \(a(t) \space m s^{–2},\) of a fast train during the first 80 seconds of motion is given by \(a(t) = – \frac{1}{20}t + 2\) where \(t\) is the time in seconds. If the train starts from rest at \(t = 0\), find the distance travelled by the train in the first minute.
▶️Answer/Explanation
Ans:
\(a(t)=-\frac{1}{20}t+2 \space\space\space v(t)=-\frac{1}{40}t^2+2t+c\)
\(v=0\) when \(t=0,\) and so \(c=0\)
Thus, \(v(t)=-\frac{1}{40}t^2+2t=-\frac{1}{40}t(t-80).\)
Since \(v(t) \ge 0\) for \(0 \le t \le 80,\) the distance travelled
= \(\int_{0}^{60}v(t)dt\)
= \(\left [ -\frac{1}{120}t^3+t^2\right ]_{0}^{60}\)
=\(60^2(1-\frac{1}{2})\)
=\(1800m.\)
Question
The velocity, \(v\), of an object, at a time \(t\), is given by \(v = k e^{-\frac{t}{2}}\), where \(t\) is in seconds and \(v\) is in \(ms^{–1}\). Find the distance travelled between \(t = 0\) and \(t = a\).
▶️Answer/Explanation
Ans:
Total distance = \(k\int_{0}^{a}e^{-\frac{t}{2}}dt\)
=\(-2k[e^{-\frac{t}{2}}]_{0}^{a}=-2k(e^{-\frac{a}{2}}-1)\) metres (or equivalent e.g. \(2k(1-e^{-\frac{a}{2}})\)
