(i)

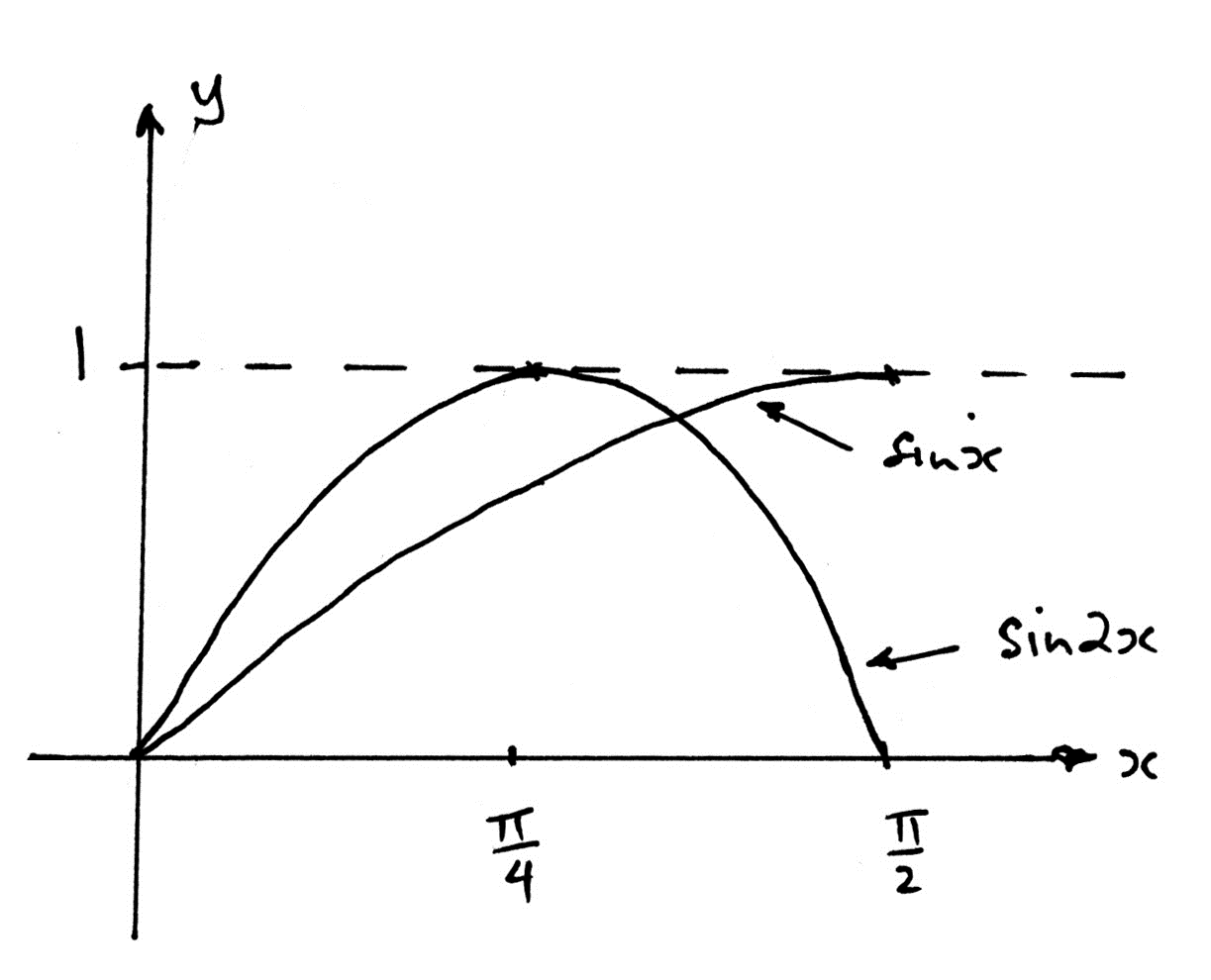A2

Note: Award A1 for correct \( \sin x \), A1 for correct \( \sin 2x \).

Note: Award A1A0 for two correct shapes with \( \frac{\pi}{2} \) and/or 1 missing.

Note: Condone graph outside the domain.

(ii) Solve \( \sin 2x = \sin x \), \( 0 \leqslant x \leqslant \frac{\pi}{2} \).

\( 2 \sin x \cos x – \sin x = 0 \) M1

\( \sin x (2 \cos x – 1) = 0 \)

\( \sin x = 0 \Rightarrow x = 0 \).

\( 2 \cos x – 1 = 0 \Rightarrow \cos x = \frac{1}{2} \Rightarrow x = \frac{\pi}{3} \). A1A1 N1N1

(iii) Area = \( \int_0^{\frac{\pi}{3}} (\sin 2x – \sin x) \, dx \) M1

Note: Award M1 for an integral with limits, with \( \sin x \) and \( \sin 2x \) subtracted in either order.

\( = \left[ -\frac{1}{2} \cos 2x + \cos x \right]_0^{\frac{\pi}{3}} \) A1

\( = \left( -\frac{1}{2} \cos \frac{2\pi}{3} + \cos \frac{\pi}{3} \right) – \left( -\frac{1}{2} \cos 0 + \cos 0 \right) \) (M1)

\( = \left( -\frac{1}{2} \cdot \left(-\frac{1}{2}\right) + \frac{1}{2} \right) – \left( -\frac{1}{2} \cdot 1 + 1 \right) = \frac{3}{4} – \frac{1}{2} \)

\( = \frac{1}{4} \) A1

[9 marks]

Let \( x = 4 \sin^2 \theta \), then \( \frac{dx}{d\theta} = 8 \sin \theta \cos \theta \), so \( dx = 8 \sin \theta \cos \theta \, d\theta \). M1

Limits: When \( x = 0 \), \( \sin^2 \theta = 0 \Rightarrow \theta = 0 \); when \( x = 1 \), \( 4 \sin^2 \theta = 1 \Rightarrow \sin^2 \theta = \frac{1}{4} \Rightarrow \theta = \frac{\pi}{6} \). A1

Substitute: \( \int_0^1 \sqrt{\frac{x}{4 – x}} \, dx = \int_0^{\frac{\pi}{6}} \sqrt{\frac{4 \sin^2 \theta}{4 – 4 \sin^2 \theta}} \cdot 8 \sin \theta \cos \theta \, d\theta \).

\( = \int_0^{\frac{\pi}{6}} \sqrt{\frac{4 \sin^2 \theta}{4 (1 – \sin^2 \theta)}} \cdot 8 \sin \theta \cos \theta \, d\theta = \int_0^{\frac{\pi}{6}} 8 \sin^2 \theta \, d\theta \). A1

Use identity: \( \sin^2 \theta = \frac{1 – \cos 2\theta}{2} \), so \( \int 8 \sin^2 \theta \, d\theta = \int 4 (1 – \cos 2\theta) \, d\theta \). M1

\( = \left[ 4\theta – 2 \sin 2\theta \right]_0^{\frac{\pi}{6}} \) A1

\( = \left( 4 \cdot \frac{\pi}{6} – 2 \sin \frac{\pi}{3} \right) – 0 = \frac{2\pi}{3} – 2 \cdot \frac{\sqrt{3}}{2} = \frac{2\pi}{3} – \sqrt{3} \). (M1)A1

[8 marks]

(i)

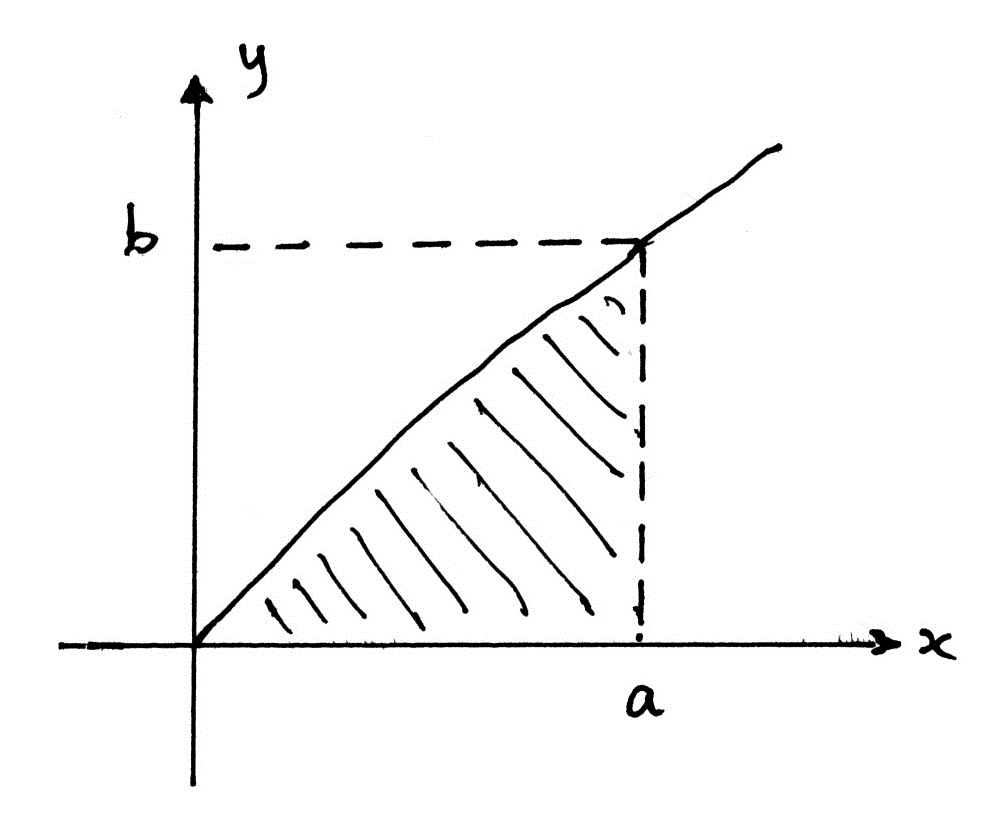M1

From the diagram, the shaded area under \( f(x) \) from 0 to \( a \) is \( \int_0^a f(x) \, dx \).

The area of the rectangle is \( ab \), and the area under \( f^{-1}(y) \) from 0 to \( b \) is \( \int_0^b f^{-1}(y) \, dy \).

Thus: \( \int_0^a f(x) \, dx = ab – \int_0^b f^{-1}(x) \, dx \). R1 AG

(ii) Let \( f(x) = \arcsin \left( \frac{x}{4} \right) \). Then \( f^{-1}(x) = 4 \sin x \). A1

Given \( f(0) = \arcsin(0) = 0 \), \( f(2) = \arcsin \left( \frac{2}{4} \right) = \arcsin \left( \frac{1}{2} \right) = \frac{\pi}{6} \), so \( a = 2 \), \( b = \frac{\pi}{6} \).

Using part (i): \( \int_0^2 \arcsin \left( \frac{x}{4} \right) \, dx = 2 \cdot \frac{\pi}{6} – \int_0^{\frac{\pi}{6}} 4 \sin x \, dx \). M1A1

Note: Award A1 for the limit \( \frac{\pi}{6} \), A1 for correct setup.

\( \int 4 \sin x \, dx = -4 \cos x \).

\( \int_0^{\frac{\pi}{6}} 4 \sin x \, dx = \left[ -4 \cos x \right]_0^{\frac{\pi}{6}} = -4 \cos \frac{\pi}{6} + 4 \cos 0 = -4 \cdot \frac{\sqrt{3}}{2} + 4 = -2 \sqrt{3} + 4 \). A1

Thus: \( \int_0^2 \arcsin \left( \frac{x}{4} \right) \, dx = \frac{\pi}{3} – (-2 \sqrt{3} + 4) = \frac{\pi}{3} + 2 \sqrt{3} – 4 \). A1

Note: Award no marks for methods using integration by parts.

[8 marks]