IB Mathematics AHL 5.18 differential equations AA HL Paper 3 - Exam Style Questions
Question
This problem explores the geometric properties of a family of rational functions and their relationship to the solutions of a specific homogeneous differential equation.
Consider the curve defined by the function \( f(x) = \frac{x(x^2 – 16)}{x^2 + 16} \).
(a) (i) Sketch the graph of \( y = f(x) \) for the domain \( -10 \le x \le 10 \).
(ii) Identify the coordinates of all \( x \)-intercepts.
(iii) Find the coordinates of the local maximum and local minimum points.
(b) By considering \( f(-x) \), determine if the function is odd, even, or neither. Provide a justification.
Now, consider the broader family of curves defined by \( f(x) = \frac{x(x^2 – A)}{x^2 + A} \), where \( A > 0 \).
(c) Show through differentiation that the gradient of the curve at \( x = \sqrt{A} \) is constant for any value of \( A \).
(d) (i) Confirm the identity \( x – \frac{2Ax}{x^2 + A} = \frac{x(x^2 – A)}{x^2 + A} \).
(ii) Determine the equation of the oblique (slant) asymptote.
(iii) Find the coordinates of the point on the curve where the tangent is parallel to this oblique asymptote.
Consider the differential equation \( x^2 \frac{dy}{dx} = x(x+y) – y^2 \), for \( x \neq 0 \) and \( y \neq \pm x \).
Using the substitution \( y = vx \), this equation transforms into \( x \frac{dv}{dx} = 1 – v^2 \).
(e) Use partial fractions to demonstrate that \( \int \frac{1}{1-v^2} \, dv = \frac{1}{2} \ln \left| \frac{A(1+v)}{1-v} \right| \), where \( A \) is a positive constant.
(f) Hence, show that the general solution to the differential equation can be written as \( x^2 = \left| \frac{A(x+y)}{x-y} \right| \).
(g) For the case where \( \frac{A(x+y)}{x-y} > 0 \), prove that the solution is the rational function \( y = \frac{x(x^2 – A)}{x^2 + A} \).
Most-appropriate topic codes (IB Mathematics AA AHL):
• AHL 5.12: Higher derivatives and notation — part (c)
• AHL 5.18: Solution of homogeneous differential equations using \( y=vx \) — parts (e), (f), (g)
• AHL 1.11: Use of partial fractions to rearrange the integrand — part (e)
• AHL 1.15: Proof and formal logic in mathematical arguments — parts (b), (c), (g)
▶️ Answer/Explanation
(a) Graphing and Key Features
(i) Sketch: 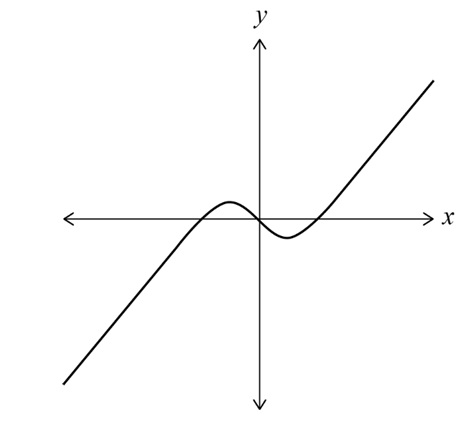
Shape: cubic-type rational function passing through origin, with \( 2 \) turning points and \( 3 \) \( x \)-intercepts. Graph approaches oblique asymptote \( y = x \) for large \( |x| \).
(ii)
\( x \)-intercepts occur when \( y = 0 \): \( x(x^2 – 16) = 0 \implies x = 0, x = \pm 4 \).
Coordinates: \( (-4, 0), (0, 0), (4, 0) \).
(iii)
Using calculus (or technology): \( f'(x) = \frac{(x^2 + 16)(3x^2 – 16) – 2x(x^3 – 16x)}{(x^2 + 16)^2} \).
Solving \( f'(x) = 0 \) gives critical points at approximately \( x \approx \pm 1.94 \).
Local maximum at \( (-1.94, 1.20) \).
Local minimum at \( (1.94, -1.20) \).
(b)
Test \( f(-x) \): \( f(-x) = \frac{(-x)((-x)^2 – 16)}{(-x)^2 + 16} = \frac{-x(x^2 – 16)}{x^2 + 16} = -f(x) \).
The function is odd because \( f(-x) = -f(x) \).
(c)
Using quotient rule: \( f'(x) = \frac{(x^2 + A)(3x^2 – A) – 2x(x^3 – Ax)}{(x^2 + A)^2} \).
At \( x = \sqrt{A} \):
Numerator: \( (A + A)(3A – A) – 2\sqrt{A}(A\sqrt{A} – A\sqrt{A}) = (2A)(2A) – 0 = 4A^2 \).
Denominator: \( (A + A)^2 = (2A)^2 = 4A^2 \).
Thus \( f'(\sqrt{A}) = \frac{4A^2}{4A^2} = 1 \), independent of \( A \).
(d)
(i)
Combine terms over common denominator: \( x – \frac{2Ax}{x^2 + A} = \frac{x(x^2 + A) – 2Ax}{x^2 + A} = \frac{x^3 + Ax – 2Ax}{x^2 + A} = \frac{x^3 – Ax}{x^2 + A} = \frac{x(x^2 – A)}{x^2 + A} \).
(ii)
For large \( |x| \), \( \frac{2Ax}{x^2 + A} \to 0 \), so \( y \to x \).
Oblique asymptote: \( y = x \).
(iii)
Tangent parallel to asymptote when \( f'(x) = 1 \).
From (c), \( f'(\sqrt{A}) = 1 \).
Point: \( (\sqrt{A}, 0) \).
(e)
Partial fractions: \( \frac{1}{1 – v^2} = \frac{1}{(1 – v)(1 + v)} = \frac{1/2}{1 + v} + \frac{1/2}{1 – v} \).
Integrate: \( \int \frac{1}{1 – v^2} \, dv = \frac{1}{2} \ln|1 + v| – \frac{1}{2} \ln|1 – v| + C = \frac{1}{2} \ln\left| \frac{1 + v}{1 – v} \right| + C \).
Let \( C = \frac{1}{2} \ln A \).
Then \( \int \frac{1}{1 – v^2} \, dv = \frac{1}{2} \ln\left| \frac{A(1 + v)}{1 – v} \right| \).
(f)
From \( x \frac{dv}{dx} = 1 – v^2 \), separate variables: \( \int \frac{1}{1 – v^2} \, dv = \int \frac{1}{x} \, dx \).
Using result from (e): \( \frac{1}{2} \ln\left| \frac{A(1 + v)}{1 – v} \right| = \ln|x| \implies \ln\left| \frac{A(1 + v)}{1 – v} \right|^{1/2} = \ln|x| \).
Exponentiate: \( \left| \frac{A(1 + v)}{1 – v} \right|^{1/2} = |x| \implies \frac{A(1 + v)}{1 – v} = x^2 \).
Substitute \( v = \frac{y}{x} \): \( \frac{A(1 + y/x)}{1 – y/x} = x^2 \implies \frac{A(x + y)}{x – y} = x^2 \).
Taking absolute values gives the required form.
(g)
Starting from \( x^2 = \frac{A(x + y)}{x – y} \) (since the expression is positive):
\( x^2(x – y) = A(x + y) \implies x^3 – x^2 y = Ax + Ay \).
Collect \( y \) terms: \( x^3 – Ax = x^2 y + Ay = y(x^2 + A) \).
Solve for \( y \): \( y = \frac{x(x^2 – A)}{x^2 + A} \).
This matches the given family of curves, confirming it is a solution to the differential equation.
