IB Mathematics AHL 5.13The evaluation of limits AA HL Paper 3
Question
This question investigates a ratio of lengths found from the line passing through the points of inflection of a quartic curve of the form $y=x^4-mx^3+nx$.
The curve $y=x^4-3x^3+3x$ has points of inflection at B and C. The line passing through B and C intersects the curve again at points A and D. This is shown in the following graph.
(a) Find $\frac{d^2y}{dx^2}$.
(b) Find the coordinates of B and C.
(c) Show that the equation of the line through B and C is $y = -0.375x$.
(d) Find, correct to three decimal places, the $x$-coordinate of D.
Now consider the general curve $y = x^4 – mx^3 + nx$, where $m, n \in \mathbb{R}$ and $m > 0$.
(e) Find the $x$-coordinates of the two points of inflection in terms of $m$.
Let these points of inflection be B and C. The line passing through B and C intersects the curve again at points A and D. Let $x_a$ be the $x$-coordinate of point A, and similarly for $x_b, x_c$, and $x_d$. It is given that $x_a < x_b < x_c < x_d$.
(f) (i) Write down the coordinates of B.
(ii) Find, in terms of $m$ and $n$, the coordinates of C.
(g) Show that the equation of the line through B and C is $y = \left (-\frac{m^3}{8} + n\right )x$.
(h) Show that $x_A = \frac{m}{4} – \frac{m}{4}\sqrt{5}$.
(i) Hence, find the exact value of $\frac{x_B – x_A}{x_C – x_B}$.
▶️Answer/Explanation
Detailed solution
Part (a): First, compute the first derivative:
Given
\[
y = x^4 – 3x^3 + 3x
\]
\[
\frac{dy}{dx} = 4x^3 – 9x^2 + 3
\]
Now, the second derivative:
\[
\frac{d^2y}{dx^2} = \frac{d}{dx} (4x^3 – 9x^2 + 3) = 12x^2 – 18x
\]
\[
= 6x(2x – 3)
\]
So, the second derivative is:
\[
\frac{d^2y}{dx^2} = 6x(2x – 3)
\]
Part (b): Points of inflection occur where the second derivative is zero and changes sign (indicating a change in concavity).
Set the second derivative to zero:
\[
6x(2x – 3) = 0
\]
\[
x = 0 \quad \text{or} \quad 2x – 3 = 0 \Rightarrow x = \frac{3}{2}
\]
Check for concavity change:
– For \( x < 0 \), say \( x = -1 \):
\[
\frac{d^2y}{dx^2} = 6(-1)(2(-1) – 3) = 6(-1)(-5) = 30 > 0 \quad (\text{concave up})
\]
– For \( 0 < x < \frac{3}{2} \), say \( x = 1 \):
\[
\frac{d^2y}{dx^2} = 6(1)(2(1) – 3) = 6(1)(-1) = -6 < 0 \quad (\text{concave down})
\]
– For \( x > \frac{3}{2} \), say \( x = 2 \):
\[
\frac{d^2y}{dx^2} = 6(2)(2(2) – 3) = 6(2)(1) = 12 > 0 \quad (\text{concave up})
\]
The second derivative changes sign at both points, confirming they are points of inflection.
Compute the \( y \)-coordinates:
– At \( x = 0 \):
\[
y = 0^4 – 3(0)^3 + 3(0) = 0
\]
So, one point (say B) is \( (0, 0) \).
– At \( x = \frac{3}{2} \):
\[
y = \left(\frac{3}{2}\right)^4 – 3\left(\frac{3}{2}\right)^3 + 3\left(\frac{3}{2}\right)
\]
\[
= \frac{81}{16} – 3 \cdot \frac{27}{8} + \frac{9}{2}
\]
\[
= \frac{81}{16} – \frac{162}{16} + \frac{72}{16} = \frac{81 – 162 + 72}{16} = -\frac{9}{16}
\]
So, the other point (say C) is \( \left(\frac{3}{2}, -\frac{9}{16}\right) \).
From the graph, B is at the origin, and C is to the right with a negative \( y \)-coordinate, which matches:
– B: \( (0, 0) \)
– C: \( \left(\frac{3}{2}, -\frac{9}{16}\right) \)
Part (c): Find the slope of the line through B \( (0, 0) \) and C \( \left(\frac{3}{2}, -\frac{9}{16}\right) \):
\[
m = \frac{-\frac{9}{16} – 0}{\frac{3}{2} – 0} = \frac{-\frac{9}{16}}{\frac{3}{2}} = -\frac{9}{16} \cdot \frac{2}{3} = -\frac{18}{48} = -\frac{3}{8}
\]
The line passes through the origin, so its equation is:
\[
y = -\frac{3}{8} x
\]
Hence, the line is \( y = -0.375x \). Hence proved
Part (d): Finding the \( x \)-coordinate of D,
Using the line \( y = -0.375x \), substitute into the curve:
\[
-0.375x = x^4 – 3x^3 + 3x
\]
\[
x^4 – 3x^3 + 3x + 0.375x = 0
\]
\[
x^4 – 3x^3 + 3.375x = 0
\]
\[
x (x^3 – 3x^2 + 3.375) = 0
\]
Roots:
– \( x = 0 \) (point B)
– Solve: \( x^3 – 3x^2 + 3.375 = 0 \)
Since \( 0.375 = \frac{3}{8} \), we have:
\[
3.375 = 3 + \frac{3}{8} = \frac{27}{8}
\]
\[
x^3 – 3x^2 + \frac{27}{8} = 0
\]
\[
8x^3 – 24x^2 + 27 = 0
\]
Test \( x = \frac{3}{2} \) (point C):
\[
8\left(\frac{3}{2}\right)^3 – 24\left(\frac{3}{2}\right)^2 + 27 = 8 \cdot \frac{27}{8} – 24 \cdot \frac{9}{4} + 27 = 27 – 54 + 27 = 0
\]
So, \( x = \frac{3}{2} \) is a root. Factor using synthetic division:
– Coefficients: \( 8, -24, 0, 27 \)
– Root: \( \frac{3}{2} \)
\[
\begin{array}{r|rrrr}
\frac{3}{2} & 8 & -24 & 0 & 27 \\
& & 12 & -18 & -27 \\
\hline
& 8 & -12 & -18 & 0 \\
\end{array}
\]
Quotient: \( 8x^2 – 12x – 18 \), so:
\[
(x – \frac{3}{2}) (8x^2 – 12x – 18) = 0
\]
\[
8x^2 – 12x – 18 = 0 \quad \Rightarrow \quad 4x^2 – 6x – 9 = 0
\]
Solve the quadratic:
\[
x = \frac{6 \pm \sqrt{36 + 144}}{8} = \frac{6 \pm \sqrt{180}}{8} = \frac{6 \pm 6\sqrt{5}}{8} = \frac{3 \pm 3\sqrt{5}}{4}
\]
\[
\sqrt{5} \approx 2.236 \quad \text{so} \quad 3\sqrt{5} \approx 6.708
\]
– \( x = \frac{3 + 3\sqrt{5}}{4} \approx \frac{9.708}{4} \approx 2.427 \)
– \( x = \frac{3 – 3\sqrt{5}}{4} \approx \frac{-3.708}{4} \approx -0.927 \)
From the graph, D is to the right of C (\( x = \frac{3}{2} \)), so:
\[
x_D \approx 2.427
\]
To three decimal places, \( x_D = 2.427 \).
Part (e): To find the \( x \)-coordinates of the points of inflection for \( y = x^4 – mx^3 + nx \)
\[
y = x^4 – mx^3 + nx
\]
\[
\frac{dy}{dx} = 4x^3 – 3mx^2 + n
\]
\[
\frac{d^2y}{dx^2} = 12x^2 – 6mx = 6x(2x – m)
\]
Set the second derivative to zero:
\[
6x(2x – m) = 0
\]
\[
x = 0 \quad \text{or} \quad 2x – m = 0 \Rightarrow x = \frac{m}{2}
\]
Check concavity:
– For \( x < 0 \), \( \frac{d^2y}{dx^2} > 0 \)
– For \( 0 < x < \frac{m}{2} \), \( \frac{d^2y}{dx^2} < 0 \)
– For \( x > \frac{m}{2} \), \( \frac{d^2y}{dx^2} > 0 \)
So, the \( x \)-coordinates of the points of inflection are:
\[
x = 0 \quad \text{and} \quad x = \frac{m}{2}
\]
Part (f)(i): Coordinates of B
Assume B is the inflection point at \( x = 0 \):
\[
y = 0^4 – m(0)^3 + n(0) = 0
\]
\[
B = (0, 0)
\]
Part (f)(ii): Coordinates of C in terms of \( m \) and \( n \)
C is at \( x = \frac{m}{2} \):
\[
y = \left(\frac{m}{2}\right)^4 – m\left(\frac{m}{2}\right)^3 + n\left(\frac{m}{2}\right)
\]
\[
= \frac{m^4}{16} – m \cdot \frac{m^3}{8} + \frac{nm}{2}
\]
\[
= \frac{m^4}{16} – \frac{m^4}{8} + \frac{nm}{2} = \frac{m^4}{16} – \frac{2m^4}{16} + \frac{8nm}{16} = \frac{-m^4 + 8nm}{16}
\]
\[
C = \left( \frac{m}{2}, \frac{-m^4 + 8nm}{16} \right)
\]
Part (g): Slope through B \( (0, 0) \) and C:
\[
m_{\text{slope}} = \frac{\frac{-m^4 + 8nm}{16} – 0}{\frac{m}{2} – 0} = \frac{\frac{-m^4 + 8nm}{16}}{\frac{m}{2}} = \frac{-m^4 + 8nm}{16} \cdot \frac{2}{m} = \frac{-m^4 + 8nm}{8m} = -\frac{m^3}{8} + n
\]
Line equation:
\[
y = \left(-\frac{m^3}{8} + n\right)x
\]
This matches the given form, confirming the result.
Part (h): Substitute the line \( y = \left(-\frac{m^3}{8} + n\right)x \) into the curve:
\[
\left(-\frac{m^3}{8} + n\right)x = x^4 – mx^3 + nx
\]
\[
x^4 – mx^3 + nx – \left(-\frac{m^3}{8} + n\right)x = 0
\]
\[
x^4 – mx^3 + \left(n + \frac{m^3}{8} – n\right)x = 0
\]
\[
x^4 – mx^3 + \frac{m^3}{8} x = 0
\]
\[
x \left( x^3 – mx^2 + \frac{m^3}{8} \right) = 0
\]
Roots:
– \( x = 0 \) (B)
– \( x^3 – mx^2 + \frac{m^3}{8} = 0 \)
Test \( x = \frac{m}{2} \) (C):
\[
\left(\frac{m}{2}\right)^3 – m\left(\frac{m}{2}\right)^2 + \frac{m^3}{8} = \frac{m^3}{8} – \frac{m^3}{4} + \frac{m^3}{8} = \frac{m^3}{8} – \frac{m^3}{4} + \frac{m^3}{8} = 0
\]
Factor:
\[
(x – \frac{m}{2}) (x^2 – \frac{m}{2} x – \frac{m^2}{4}) = 0
\]
\[
x^2 – \frac{m}{2} x – \frac{m^2}{4} = 0
\]
\[
x = \frac{\frac{m}{2} \pm \sqrt{\frac{m^2}{4} + m^2}}{2} = \frac{\frac{m}{2} \pm \frac{m \sqrt{5}}{2}}{2} = \frac{m}{4} (1 \pm \sqrt{5})
\]
– \( x = \frac{m}{4} (1 + \sqrt{5}) \)
– \( x = \frac{m}{4} (1 – \sqrt{5}) = \frac{m}{4} – \frac{m}{4} \sqrt{5} \)
Since \( x_A < x_B = 0 \), and \( 1 – \sqrt{5} < 0 \), we have:
\[
x_A = \frac{m}{4} – \frac{m}{4} \sqrt{5}
\]
Part (i): Given:
– \( x_A = \frac{m}{4} – \frac{m}{4} \sqrt{5} \)
– \( x_B = 0 \)
– \( x_C = \frac{m}{2} \)
\[
x_B – x_A = 0 – \left( \frac{m}{4} – \frac{m}{4} \sqrt{5} \right) = \frac{m}{4} (\sqrt{5} – 1)
\]
\[
x_C – x_B = \frac{m}{2} – 0 = \frac{m}{2}
\]
\[
\frac{x_B – x_A}{x_C – x_B} = \frac{\frac{m}{4} (\sqrt{5} – 1)}{\frac{m}{2}} = \frac{m}{4} (\sqrt{5} – 1) \cdot \frac{2}{m} = \frac{\sqrt{5} – 1}{2}
\]
The exact value is:
\[
\frac{\sqrt{5} – 1}{2}
\]
……………..Markscheme…………………
Solution: –
(a)
$$\frac{dy}{dx}=4x^{3}-9x^{2}+3$$
$$\frac{d^{2}y}{dx^{2}}=12x^{2}-18x$$
(b)
valid attempt to find x-coordinates (e.g solving $12x^{2}-18x=10$ or graphing $\frac{dy}{dx}=4x^{3}-9x^{2}+3$
$$x=0,1.5(\frac{3}{2})$$
point B is $(0,0)$
point C is $(1.5,-0.5625)$
$\left [ \left ( 1.5,-0.563 \right ),\left [ \frac{3}{2},-\frac{9}{16} \right ] \right ]$
(c)
y-intercept = 0 (as line passes through (0,0))
gradient =$\frac{-0.5625}{1.5} $ $\left [ =\frac{\frac{-9}{16}}{\frac{3}{2}} \right ] $
=-0.375
so equation is y = -0.375x
(d)
$$x^4-3x^3+3x=0.375x$$
$$2.427$$
(e)
$$\frac{dy}{dx}=4x^3-3mx^2+n$$
$$\frac{d^2y}{dx^2}=12x^2-6mx$$
$$6x(2x-m)=0$$
$$x=0,\frac{m}{2}$$
(f) (i) Point B is (0,0)
(ii) $$y_c = \left(\frac{m}{2}\right)^4 – m\left(\frac{m}{2}\right)^3 + n\left(\frac{m}{2}\right) \left(=\frac{m^4}{16}-\frac{m^4}{8}+\frac{nm}{2}\right)$$
$$-\frac{m^4}{16}+\frac{m^2n}{2} \text{ OR } \frac{8m^2n-m^4}{16} \text{ OR } \frac{m}{2}\left(n-\frac{m^2}{8}\right) \text{ OR equivalent simplification}$$
$$\text {Point C is} $\left(\frac{m}{2}, -\frac{m^4}{16}+\frac{m^2n}{2}\right)$$
(g) attempt to divide their $ y_{c}$ by their $x_{c}$ OR substitute into $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$$\left[ \frac{m^{4}}{16}+\frac{nm}{2}\right ]+\frac{m}{2}$$
$$(-\frac{m^4}{16}+\frac{m^2n}{2})\times\frac{2}{m}$$
OR
equivalent manipulation leading to given answer
$$=-\frac{m^3}{8}+n$$
and y-intercept = 0.
so equation is
$$y=(-\frac{m^3}{8}+n)x$$
(h) METHOD 1
$$x^4-mx^3+nx=-\frac{m^3}{8}x+nx$$
attempt to rearrange this equation to equal zero
$$x^4-mx^3+\frac{m^3}{8}x=0$$
recognizing their $\left ( x-x_{c} \right )$ is a factor of this expression
$$x(x-\frac{m}{2})(x^2-\frac{m}{2}x-\frac{m^2}{4})=0$$
use of quadratic formula to find roots, $x_A$ and $x_D$, of the quadratic:
$$x_A=\frac{\frac{m}{2}-\sqrt{\frac{m^2}{4}+\frac{m^2}{4}}}{2}$$
OR equivalent
$$x_A=\frac{m}{4}-\frac{m}{4}\sqrt{5}$$
METHOD 2
$$x^4-mx^3+nx=-\frac{m^3}{8}x+nx$$
$$x^4-mx^3+\frac{m^3}{8}x=0$$
$$x(x^3-mx^2+\frac{m^3}{8})=0$$
Recognise that their $x_A$ is a root of this equation
Attempt to find sum and product of roots
$$x_A+x_D=\frac{m}{2} \text{ AND } x_A\times x_D=\frac{m^2}{8}$$
$$x_A(\frac{m}{2}-x_A)=\frac{m^2}{8}$$
$$x_A^2-\frac{m}{2}x_A-\frac{m^2}{8}=0$$
use of quadratic formula to find roots, $x_A$ and $x_D$, of the quadratic:
$$x_A=\frac{\frac{m}{2}-\sqrt{\frac{m^2}{4}+\frac{m^2}{4}}}{2}$$
OR equivalent
$$x_A=\frac{m}{4}-\frac{m}{4}\sqrt{5}$$
(i)
$$\frac{0-(\frac{m}{4}-\frac{m}{4}\sqrt{5})}{\frac{m}{2}-0}$$
$$=\frac{\sqrt{5}-1}{2}$$
Question
This question asks you to investigate regular $n$-sided polygons inscribed and circumscribed in a circle, and the perimeter of these as $n$ tends to infinity, to make an approximation for $\pi$.
Let $P_i(n)$ represent the perimeter of any $n$-sided regular polygon inscribed in a circle of radius 1 unit.
Consider an equilateral triangle $A B C$ of side length, $x$ units, circumscribed about a circle of radius 1 unit and centre $\mathrm{O}$ as shown in the following diagram.
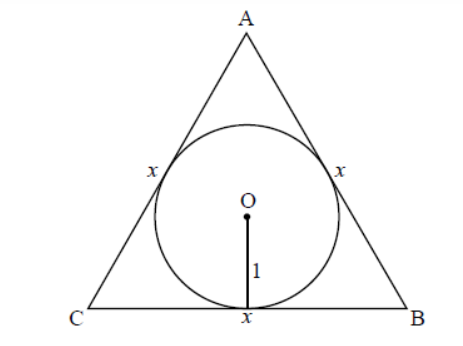
Let $P_c(n)$ represent the perimeter of any $n$-sided regular polygon circumscribed about a circle of radius 1 unit.
a. Consider an equilateral triangle $A B C$ of side length, $x$ units, inscribed in a circle of radius 1 unit and centre $O$ as shown in the following diagram.
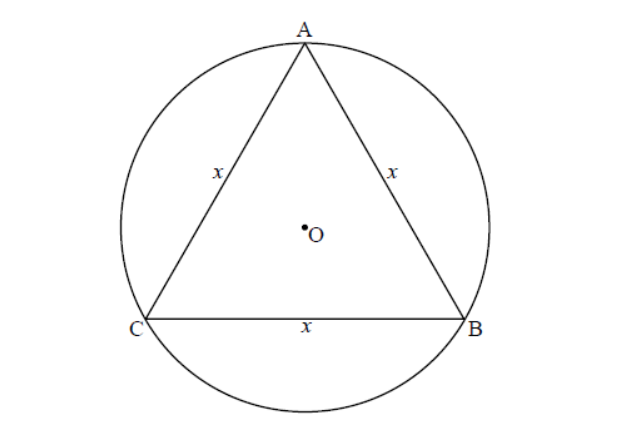
The equilateral triangle $A B C$ can be divided into three smaller isosceles triangles, each subtending an angle of $\frac{2 \pi}{3}$ at $\mathrm{O}$, as shown in the following diagram.
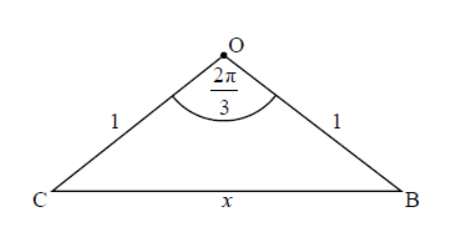
Using right-angled trigonometry or otherwise, show that the perimeter of the equilateral triangle $A B C$ is equal to $3 \sqrt{3}$ units.
b. Consider a square of side length, $x$ units, inscribed in a circle of radius 1 unit. By dividing the inscribed square into four isosceles triangles, find
[3] the exact perimeter of the inscribed square.
c. Find the perimeter of a regular hexagon, of side length, $x$ units, inscribed in a circle of radius 1 unit.
[2]
d. Show that $P_i(n)=2 n \sin \left(\frac{\pi}{n}\right)$.
[3]
e. Use an appropriate Maclaurin series expansion to find $\lim _{n \rightarrow \infty} P_i(n)$ and interpret this result geometrically.
f. Show that $P_c(n)=2 n \tan \left(\frac{\pi}{n}\right)$.
g.
By writing $P_c(n)$ in the form $\frac{2 \tan \left(\frac{\pi}{n}\right)}{\frac{1}{n}}$, find $\lim _{n \rightarrow \infty} P_c(n)$.
h. Use the results from part (d) and part (f) to determine an inequality for the value of $\pi$ in terms of $n$.
[2]
i. The inequality found in part (h) can be used to determine lower and upper bound approximations for the value of $\pi$.
[3]
Determine the least value for $n$ such that the lower bound and upper bound approximations are both within 0.005 of $\pi$.
▶️Answer/Explanation
Markscheme
a. $M E T H O D 1$
consider right-angled triangle $\mathrm{OCX}$ where $\mathrm{CX}=\frac{x}{2}$
$$
\begin{aligned}
& \sin \frac{\pi}{3}=\frac{\frac{x}{2}}{1} \quad \text { MIA1 } \\
& \Rightarrow \frac{x}{2}=\frac{\sqrt{3}}{2} \Rightarrow x=\sqrt{3} \quad \text { A1 } \\
& P_i=3 \times x=3 \sqrt{3} \quad \text { AG }
\end{aligned}
$$
METHOD 2
eg use of the cosine rule $x^2=1^2+1^2-2(1)(1) \cos \frac{2 \pi}{3} \quad$ M1A1
$x=\sqrt{3} \quad$ A1
$P_i=3 \times x=3 \sqrt{3} \quad \boldsymbol{A G}$
Note: Accept use of sine rule.
[3 marks]
b. $\sin _{\frac{\pi}{4}}^{\frac{\pi}{4}}=\frac{1}{x}$ where $x=$ side of square
M1
$x=\sqrt{2} \quad$ A1
$P_i=4 \sqrt{2} \quad$ A1
[3 marks]
c. 6 equilateral triangles $\Rightarrow x=1$
A1
$P_i=6$
A1
[2 marks]
d. in right-angled triangle $\sin \left(\frac{\pi}{n}\right)=\frac{\frac{x}{2}}{1} \quad$ M1
$\Rightarrow x=2 \sin \left(\frac{\pi}{n}\right) \quad$ A1
$P_i=n \times x$
$P_i=n \times 2 \sin \left(\frac{\pi}{n}\right) \quad \boldsymbol{M} 1$
$P_i=2 n \sin \left(\frac{\pi}{n}\right) \quad$ AG
[3 marks]
e.
consider $\lim _{n \rightarrow \infty} 2 n \sin \left(\frac{\pi}{n}\right)$
use of $\sin x=x-\frac{x^3}{3 !}+\frac{x^5}{5 !}-\ldots \quad$ M1
$$
\begin{aligned}
& 2 n \sin \left(\frac{\pi}{n}\right)=2 n\left(\frac{\pi}{n}-\frac{\pi^3}{6 n^3}+\frac{\pi^5}{120 n^5}-\ldots\right) \\
& =2\left(\pi-\frac{\pi^3}{6 n^2}+\frac{\pi^5}{120 n^4}-\ldots\right) \quad \boldsymbol{A 1} \\
& \Rightarrow \lim _{n \rightarrow \infty} 2 n \sin \left(\frac{\pi}{n}\right)=2 \pi \quad \boldsymbol{A 1}
\end{aligned}
$$
(A1)
as $n \rightarrow \infty$ polygon becomes a circle of radius 1 and $P_i=2 \pi$
R1
[5 marks]
f. consider an $n$-sided polygon of side length $x$
$2 n$ right-angled triangles with angle $\frac{2 \pi}{2 n}=\frac{\pi}{n}$ at centre M1A1
opposite side $\frac{x}{2}=\tan \left(\frac{\pi}{n}\right) \Rightarrow x=2 \tan \left(\frac{\pi}{n}\right) \quad$ M1A1
Perimeter $P_c=2 n \tan \left(\frac{\pi}{n}\right) \quad$ AG
[4 marks]
g.
$$
\begin{aligned}
& \text { consider } \lim _{n \rightarrow \infty} 2 n \tan \left(\frac{\pi}{n}\right)=\lim _{n \rightarrow \infty}\left(\frac{2 \tan \left(\frac{\pi}{n}\right)}{\frac{1}{n}}\right) \\
& =\lim _{n \rightarrow \infty}\left(\frac{2 \tan \left(\frac{\pi}{n}\right)}{\frac{1}{n}}\right)=\frac{0}{0}
\end{aligned}
$$
attempt to use L’Hopital’s rule M1
$$
\begin{aligned}
& =\lim _{n \rightarrow \infty}\left(\frac{-\frac{2 \pi}{n^2} \sec ^2\left(\frac{\pi}{n}\right)}{-\frac{1}{n^2}}\right) \quad \text { A1A1 } \\
& =2 \pi
\end{aligned}
$$
[5 marks]
h. $P_i<2 \pi<P_c$
$$
\begin{aligned}
& 2 n \sin \left(\frac{\pi}{n}\right)<2 \pi<2 n \tan \left(\frac{\pi}{n}\right) \quad \text { M1 } \\
& n \sin \left(\frac{\pi}{n}\right)<\pi<n \tan \left(\frac{\pi}{n}\right) \quad \text { A1 } \\
& {[2 \text { marks] }}
\end{aligned}
$$
i. attempt to find the lower bound and upper bound approximations within 0.005 of $\pi$
(M1)
$$
n=46 \quad \text { A2 }
$$
[3 marks]