IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 11.1 Electromagnetic induction
Topic 11 Weightage : 5 %
All Questions for Topic 11.1 – Electromotive force (emf) , Magnetic flux and magnetic flux linkage , Faraday’s law of induction , Lenz’s law
Question
The diagram shows an alternating current generator with a rectangular coil rotating at a constant frequency in a uniform magnetic field.
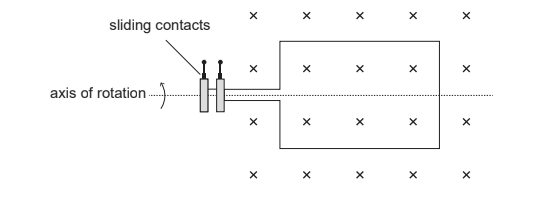
(a) Explain, by reference to Faraday’s law of induction, how an electromotive force (emf) is induced in the coil. [3]
▶️Answer/Explanation
Ans:
there is a magnetic flux «linkage» in the coil / coil cuts magnetic field ✓
this flux «linkage» changes as the angle varies/coil rotates ✓
«Faraday’s law» connects induced emf with rate of change of flux «linkage» with time ✓
Part 2 Electromagnetic induction
The diagram shows a horizontal metal rod suspended by two vertical insulated springs.
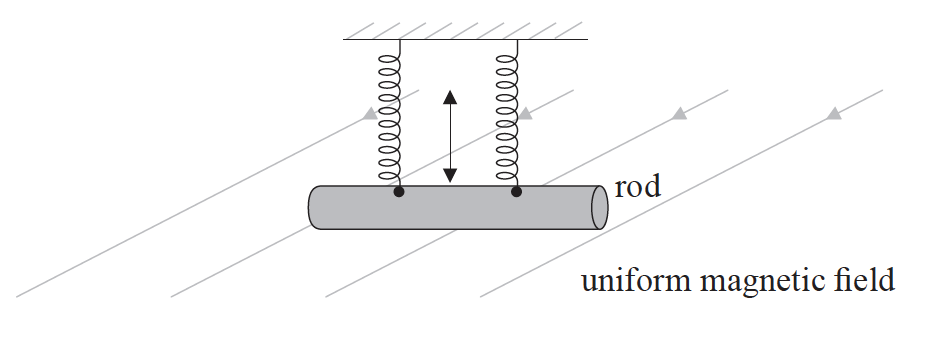
The rod moves vertically up and down with simple harmonic motion with a time period T at right angles to a uniform magnetic field.
The diagram shows the variation with time t of the vertical displacement x of the rod.
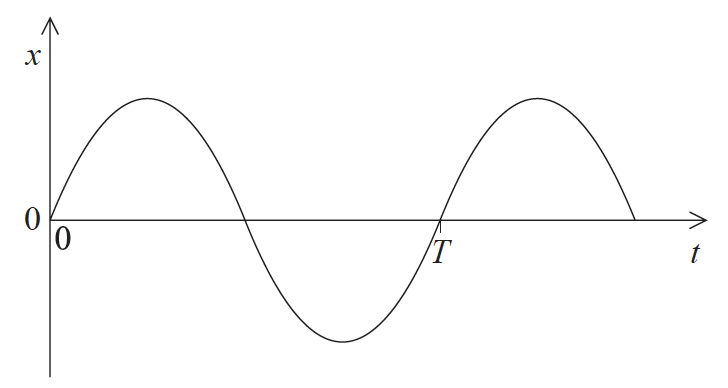
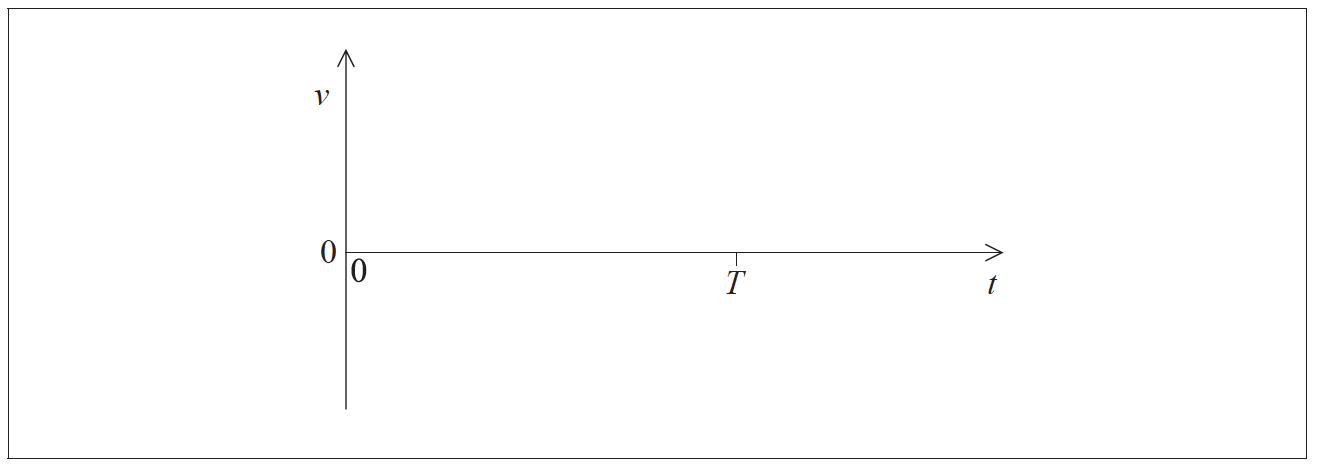
a.On the axes provided, draw a graph to show
(i) the variation with time t of the vertical velocity v of the rod.
(ii) the variation with time t of the emf generated between the ends of the rod.
Determine the magnitude of the maximum emf εmax ¬between the ends of the rod.[3]
State and explain the changes to the variation with time t of the emf \(\varepsilon \)¬ generated as a result of this change in frequency.[4]
▶️Answer/Explanation
Markscheme
a.
(i)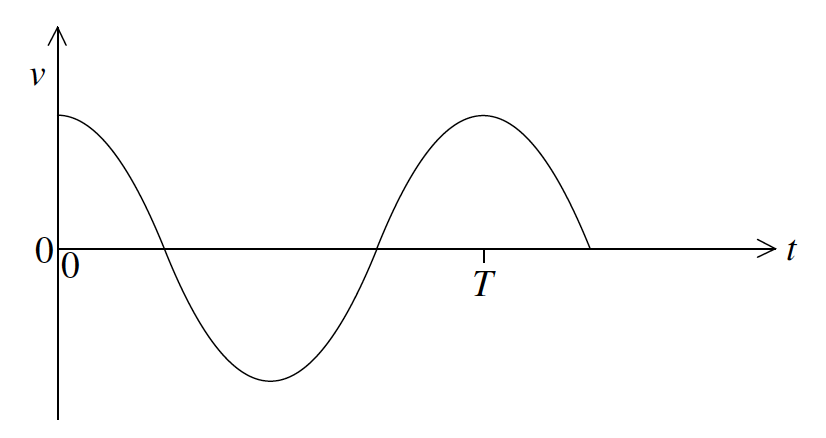
cosine wave same frequency as original;
phase correct;
(ii) emf in phase or antiphase with answer to (a)(i);
ε=58×10-6×0.18×1.29;
13.5 μV;
because same change of flux in half the time / because frequency of emf must equal frequency of oscillation;
maximum emf doubles;
maximum speed doubles / flux changes at twice rate;
This question is about induced electromotive force (emf).
A loop of copper wire in a region of uniform magnetic field is rotated about a horizontal axis.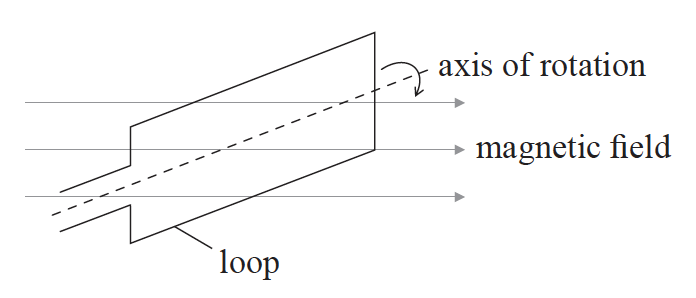
a.The magnitude of the magnetic field strength is B and the area of the loop is A.
(i) State the minimum value and the maximum value of the magnetic flux linking the loop.
(ii) Outline with reference to Faraday’s law why, if the speed of rotation of the loop is increased, the maximum emf induced in the loop is increased.[4]
(i) Explain what is meant by the rms value of a sinusoidal current.
(ii) Determine the maximum power dissipated in the resistor[4]
▶️Answer/Explanation
Markscheme
a.
(i) minimum: zero / –BA (minus sign required)
maximum: BA } (both needed)
(ii) Look for these main points:
(Faraday’s law states that the) induced emf equals/is proportional to the rate of change of flux/flux linkage; { (must see induced)
speed greater so time for change shorter / flux (linkage) is unchanged;
greater rate of change (of flux etc) gives a greater (induced) emf;
Award [1 max] if answer states flux (linkage) change is larger.
(i) (equivalent) direct current;
dissipating same power in a (fixed) resistor (as the rms current);
(ii) maximum current \( = \left( {\sqrt 2 \times 2.3 = } \right)3.2/3.3{\rm{mA}}\);
maximum power = (3.32×15=)0.16mW;
