IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 11.3 Capacitance
Topic 11 Weightage : 5 %
All Questions for Topic 11.3 – Capacitance , Dielectric materials , Capacitors in series and parallel , Resistor-capacitor (RC) series circuits , Time constant
Question
A student makes a parallel-plate capacitor of capacitance 68 nF from aluminium foil and plastic film by inserting one sheet of plastic film between two sheets of aluminium foil.
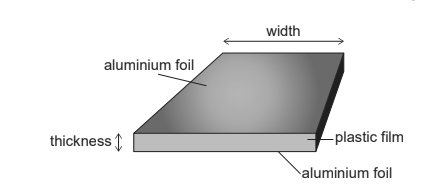 μ
μThe aluminium foil and the plastic film are 450 mm wide.
The plastic film has a thickness of 55 μm and a permittivity of 2.5 × 10–11 C2 N–1 m–2.
(i) Calculate the total length of aluminium foil that the student will require. [3]
(ii) The plastic film begins to conduct when the electric field strength in it exceeds 1.5 MN C–1. Calculate the maximum charge that can be stored on the capacitor. [2]
The student uses a switch to charge and discharge the capacitor using the circuit shown. The ammeter is ideal.
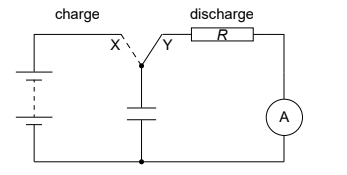
The emf of the battery is 12 V.
The resistor R in the circuit has a resistance of 1.2kΩ. Calculate the time taken for the charge on the capacitor to fall to 50 % of its fully charged value. [3]
The ammeter is replaced by a coil. Explain why there will be an induced emf in the coil while the capacitor is discharging. [2]
Suggest one change to the discharge circuit, apart from changes to the coil, thawill increase the maximum induced emf in the coil. [2]
▶️Answer/Explanation
Ans:(191)
a i length = \(\frac{d\times C}{width\times \epsilon }\) = 0.33 «m» so 0.66/0.67 «m» «as two lengths required»
a ii 1.5 ×106 ×55 ×10-6 = 83 «V» q «= CV»= 5.6 ×10-6 «C» 8. b i 0.5 = e –\(\frac{1}{Rc}\) = e \(\frac{t}{1200\times 6.8\times 10^{-8}}\) t = «- »1200 × 6.8 × 10-8 ln0.5 5.7× 10−5 «s» OR use of t=\(\frac{1}{2}\) = RC × ln2 1200×6.8×10−8× 0.693 5.7× 10−5 «s»
b ii mention of Faraday’s law indicating that changing current in discharge circuit leads to change in flux in coil/change in magnetic field «and induced emf»
b iii decrease/reduce resistance (R) OR capacitance (C)
A negatively charged thundercloud above the Earth’s surface may be modelled by a parallel plate capacitor.
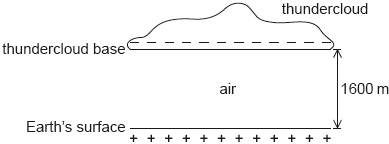
The lower plate of the capacitor is the Earth’s surface and the upper plate is the base of the thundercloud.
The following data are available.
\[\begin{array}{*{20}{l}} {{\text{Area of thundercloud base}}}&{ = 1.2 \times {{10}^8}{\text{ }}{{\text{m}}^2}} \\ {{\text{Charge on thundercloud base}}}&{ = -25{\text{ C}}} \\ {{\text{Distance of thundercloud base from Earth’s surface}}}&{ = 1600{\text{ m}}} \\ {{\text{Permittivity of air}}}&{ = 8.8 \times {{10}^{ – 12}}{\text{ F }}{{\text{m}}^{ – 1}}} \end{array}\]
Lightning takes place when the capacitor discharges through the air between the thundercloud and the Earth’s surface. The time constant of the system is 32 ms. A lightning strike lasts for 18 ms.
a. Show that the capacitance of this arrangement is C = 6.6 × 10–7 F.[1]
▶️Answer/Explanation
Markscheme
a.
C = «ε\(\frac{A}{d}\) =» 8.8 × 10–12 × \(\frac{{1.2 \times {{10}^8}}}{{1600}}\)
«C = 6.60 × 10–7 F»
[1 mark]
V = «\(\frac{Q}{C}\) =» \(\frac{{25}}{{6.6 \times {{10}^{ – 7}}}}\)
V = 3.8 × 107 «V»
Award [2] for a bald correct answer
[2 marks]
ALTERNATIVE 1
E = «\(\frac{1}{2}\)QV =» \(\frac{1}{2}\) × 25 × 3.8 × 107
E = 4.7 × 108 «J»
ALTERNATIVE 2
E = «\(\frac{1}{2}\)CV2 =» \(\frac{1}{2}\) × 6.60 × 10–7 × (3.8 × 107)2
E = 4.7 × 108 «J» / 4.8 × 108 «J» if rounded value of V used
Award [2] for a bald correct answer
Allow ECF from (b)(i)
[2 marks]
Q = «\({Q_0}{e^{ – \frac{t}{\tau }}}\) =» 25 × \({e^{ – \frac{{18}}{{32}}}}\)
Q = 14.2 «C»
charge delivered = Q = 25 – 14.2 = 10.8 «C»
«≈ –11 C»
Final answer must be given to at least 3 significant figures
[3 marks]
I «= \(\frac{{\Delta Q}}{{\Delta t}} = \frac{{11}}{{18 \times {{10}^{ – 3}}}}\)» ≈ 610 «A»
Accept an answer in the range 597 − 611 «A»
[1 mark]
the base of the thundercloud must be parallel to the Earth surface
OR
the base of the thundercloud must be flat
OR
the base of the cloud must be very long «compared with the distance from the surface»
[1 mark]
A capacitor consists of two parallel square plates separated by a vacuum. The plates are 2.5 cm × 2.5 cm squares. The capacitance of the capacitor is 4.3 pF.
a. Calculate the distance between the plates. [1]
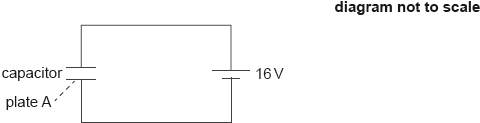
Calculate the magnitude and the sign of the charge on plate A when the capacitor is fully charged. [2]
Explain whether the magnitude of the charge on plate A increases, decreases or stays constant. [2]
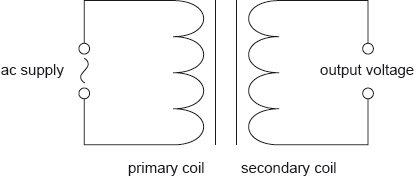
The transformer has 100 turns in the primary coil and 1200 turns in the secondary coil. The peak value of the voltage of the ac supply is 220 V. Determine the root mean square (rms) value of the output voltage. [3]
▶️Answer/Explanation
Markscheme
a.
d = «\(\frac{{8.85 \times {{10}^{ – 12}} \times {{0.025}^2}}}{{4.3 \times {{10}^{ – 12}}}}\) =» 1.3 × 10–3 «m»
[1 mark]
6.9 × 10–11 «C»
negative charge/sign
[2 marks]
charge increases
because capacitance increases AND pd remains the same.
[2 marks]
ALTERNATIVE 1
εs = \(\frac{{1200}}{{100}}\) × 220
= 2640 «V»
Vrms = \(\frac{{2640}}{{\sqrt 2 }}\) = 1870 «V»
ALTERNATIVE 2
(Primary) Vrms = \(\frac{{220}}{{\sqrt 2 }}\) = 156 «V»
(Secondary) Vrms = \(\frac{{156 \times 1200}}{{100}}\)
Vrms = 1870 «V»
Allow ECF from MP1 and MP2.
Award [2] max for 12.96 V (reversing Np and Ns).
[3 marks]
step-up transformers increase voltage/step-down transformers decrease voltage
(step-up transformers increase voltage) from plants to transmission lines / (step-down transformers decrease voltage) from transmission lines to final utilizers
this decreases current (in transmission lines)
to minimize energy/power losses in transmission
[3 marks]
The electrical circuit shown is used to investigate the temperature change in a wire that is wrapped around a mercury-in-glass thermometer.
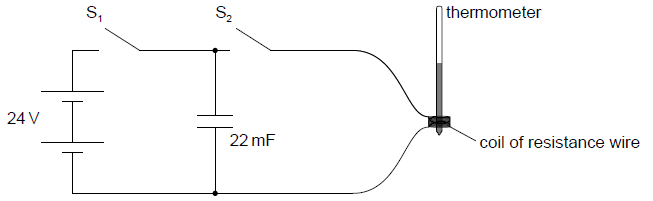
A power supply of emf (electromotive force) 24 V and of negligible internal resistance is connected to a capacitor and to a coil of resistance wire using an arrangement of two switches. Switch S1 is closed and, a few seconds later, opened. Then switch S2 is closed.
a.The capacitance of the capacitor is 22 mF. Calculate the energy stored in the capacitor when it is fully charged.[1]
▶️Answer/Explanation
Markscheme
a.
«\(\frac{1}{2}C{V^2} = \frac{1}{2} \times 0.22 \times {24^2}\)» = «J»
\(\frac{1}{{100}} = {e^{ – \frac{t}{{8.0 \times 0.022}}}}\)
\(\ln 0.01 = – \frac{t}{{8.0 \times 0.022}}\)
0.81 «s»
c = \(\frac{Q}{{m \times \Delta T}}\)
OR
\(\frac{{6.3}}{{0.00061 \times 28}}\)
370 J kg–1 K–1
Allow ECF from 3(a) for energy transferred.
Correct answer only to include correct unit that matches answer power of ten.
Allow use of g and kJ in unit but must match numerical answer, eg: 0.37 J kg–1 K–1 receives [1]
ALTERNATIVE 1
some thermal energy will be transferred to surroundings/along connecting wires/to
thermometer
estimate «of specific heat capacity by student» will be larger «than accepted value»
ALTERNATIVE 2
not all energy transferred as capacitor did not fully discharge
so estimate «of specific heat capacity by student» will be larger «than accepted value»
