IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 12.2 Nuclear physics
Topic 12 Weightage : 7 %
All Questions for Topic 12.2 – Rutherford scattering and nuclear radius , Nuclear energy levels , The neutrino , The law of radioactive decay and the decay constant
Question
The de Broglie wavelength λ of a particle accelerated close to the speed of light is approximately
λ =
where E is the energy of the particle.
A beam of electrons of energy 4.2 × 108 eV is produced in an accelerator.
(a) The electron beam is used to study the nuclear radius of carbon-12. The beam is directed from the left at a thin sample of carbon-12. A detector is placed at an angle θ relative to the direction of the incident beam.
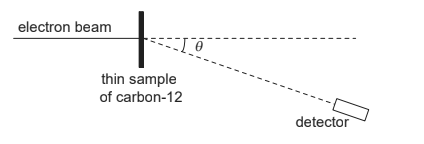
The graph shows the variation of the intensity of electrons with θ. There is a minimum of intensity for θ = θ0.
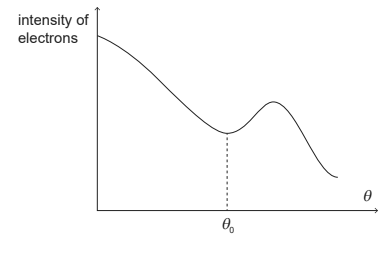
(i) Discuss how the results of the experiment provide evidence for matter waves. [2]
(ii) The accepted value of the diameter of the carbon-12 nucleus is 4.94 × 10–15 m.
Estimate the angle θ0 at which the minimum of the intensity is formed. [2]
(iii) Outline why electrons with energy of approximately 107 eV would be unsuitable for the investigation of nuclear radii. [2]
(b) Experiments with many nuclides suggest that the radius of a nucleus is proportional to A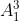
, where A is the number of nucleons in the nucleus.
Show that the density of a nucleus remains approximately the same for all nuclei. [2]
▶️Answer/Explanation
Ans
a.i
«the shape of the graph suggests that» electrons undergo diffraction «with carbon nuclei»
✓
only waves diffract ✓
a.ii
\(sin \theta_0=\frac{2.96\times10^{-15}}{4.94\times10^{-15}}=0.599\)
37 «degrees» OR 0.64/0.65 «rad» ✓
a.iii
the de Broglie wavelength of electrons is «much» longer than the size of a nucleus ✓
hence electrons would not undergo diffraction
OR
no diffraction pattern would be observed ✓
b
volume of a nucleus proportional to \(\left ( A^{\frac{1}{3}} \right )^3\) = A AND mass proportional to A ✓
the ratio \(\frac{mass}{volume}\) independent of A «hence density the same for all nuclei» ✓
Question
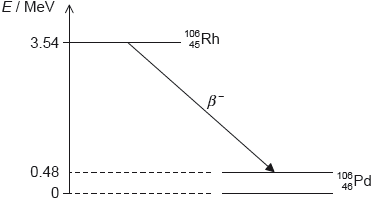
Rhodium-106 (\(_{\,\,\,45}^{106}{\text{Rh}}\)) decays into palladium-106 (\(_{\,\,\,46}^{106}{\text{Pd}}\)) by beta minus (β–) decay. The diagram shows some of the nuclear energy levels of rhodium-106 and palladium-106. The arrow represents the β– decay.
b. Bohr modified the Rutherford model by introducing the condition mvr = n\(\frac{h}{{2\pi }}\). Outline the reason for this modification. [3]
\[v = \sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \]
where k is the Coulomb constant. [1]
\[r = \frac{{{h^2}}}{{4{\pi ^2}k{m_{\text{e}}}{e^2}}}\] [2]
▶️Answer/Explanation
Markscheme
b.
the electrons accelerate and so radiate energy
they would therefore spiral into the nucleus/atoms would be unstable
electrons have discrete/only certain energy levels
the only orbits where electrons do not radiate are those that satisfy the Bohr condition «mvr = n\(\frac{h}{{2\pi }}\)»
[3 marks]
\(\frac{{{m_{\text{e}}}{v^2}}}{r} = \frac{{k{e^2}}}{{{r^2}}}\)
OR
KE = \(\frac{1}{2}\)PE hence \(\frac{1}{2}\)mev2 = \(\frac{1}{2}\frac{{k{e^2}}}{r}\)
«solving for v to get answer»
Answer given – look for correct working
[1 mark]
combining v = \(\sqrt {\frac{{k{e^2}}}{{{m_{\text{e}}}r}}} \) with mevr = \(\frac{h}{{2\pi }}\) using correct substitution
«eg \({m_e}^2\frac{{k{e^2}}}{{{m_{\text{e}}}r}}{r^2} = \frac{{{h^2}}}{{4{\pi ^2}}}\)»
correct algebraic manipulation to gain the answer
Answer given – look for correct working
Do not allow a bald statement of the answer for MP2. Some further working eg cancellation of m or r must be shown
[2 marks]
« r = \(\frac{{{{(6.63 \times {{10}^{ – 34}})}^2}}}{{4{\pi ^2} \times 8.99 \times {{10}^9} \times 9.11 \times {{10}^{ – 31}} \times {{(1.6 \times {{10}^{ – 19}})}^2}}}\)»
r = 5.3 × 10–11 «m»
[1 mark]
the energy released is 3.54 – 0.48 = 3.06 «MeV»
this is shared by the electron and the antineutrino
so the electron’s energy varies from 0 to 3.06 «MeV»
[3 marks]
the palladium nucleus emits the photon when it decays into the ground state «from the excited state»
[1 mark]
Photon energy
E = 0.48 × 106 × 1.6 × 10–19 = «7.68 × 10–14 J»
λ = «\(\frac{{hc}}{E} = \frac{{6.63 \times {{10}^{ – 34}} \times 3 \times {{10}^8}}}{{7.68 \times {{10}^{ – 14}}}}\) =» 2.6 × 10–12 «m»
Award [2] for a bald correct answer
Allow ECF from incorrect energy
[2 marks]
Question
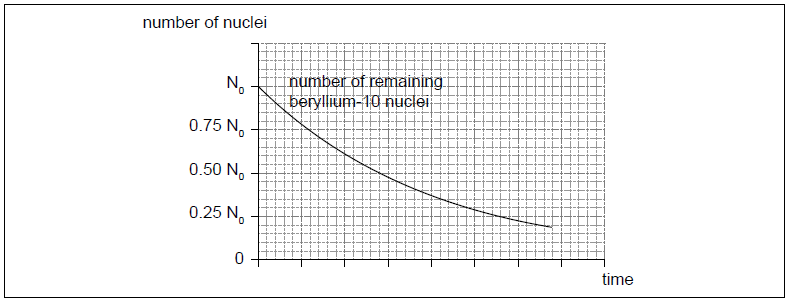
The radioactive nuclide beryllium-10 (Be-10) undergoes beta minus (β–) decay to form a stable boron (B) nuclide.
The initial number of nuclei in a pure sample of beryllium-10 is N0. The graph shows how the number of remaining beryllium nuclei in the sample varies with time.
An ice sample is moved to a laboratory for analysis. The temperature of the sample is –20 °C.
a.
Identify the missing information for this decay.
Determine, in years, the age of the sample. [3]
▶️Answer/Explanation
Markscheme
a.
\(_{{\mkern 1mu} {\mkern 1mu} 4}^{10}{\text{Be}} \to _{{\mkern 1mu} {\mkern 1mu} 5}^{10}{\text{B}} + _{ – 1}^{\,\,\,0}{\text{e}} + {\overline {\text{V}} _{\text{e}}}\)
antineutrino AND charge AND mass number of electron \(_{ – 1}^{\,\,\,0}{\text{e}}\), \(\overline {\text{V}} \)
conservation of mass number AND charge \(_{\,\,5}^{10}{\text{B}}\), \(_{{\mkern 1mu} {\mkern 1mu} 4}^{10}{\text{Be}}\)
Do not accept V.
Accept \({\bar V}\) without subscript e.
[2 marks]
λ «= \(\frac{{\ln 2}}{{1.4 \times {{10}^6}}}\)» = 4.95 × 10–7 «y–1»
rearranging of A = λN0e–λt to give –λt = ln \(\frac{{8.0 \times {{10}^{-3}} \times 365 \times 24 \times 60 \times 60}}{{4.95 \times {{10}^{-7}} \times 7.6 \times {{10}^{11}}}}\) «= –0.400»
t = \(\frac{{ – 0.400}}{{ – 4.95 \times {{10}^{ – 7}}}} = 8.1 \times {10^5}\) «y»
Allow ECF from MP1
[3 marks]
from the laboratory to the sample
conduction – contact between ice and lab surface.
OR
convection – movement of air currents
Must clearly see direction of energy transfer for MP1.
Must see more than just words “conduction” or “convection” for MP2.
[2 marks]
[N/A]
Related Links