IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 2.4 – Momentum and impulse
Topic 2 Weightage : 9 %
All Questions for Topic 2.4 – Newton’s second law expressed in terms of rate of change of momentum , Impulse and force–time graphs , Conservation of linear momentum , Elastic collisions, inelastic collisions and explosions
Question
The graph shows the variation with time t of the horizontal force F exerted on a tennis ball by a racket.
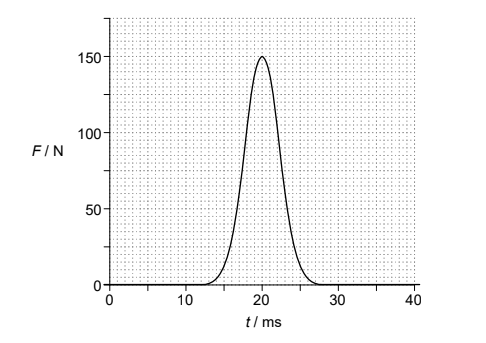
The tennis ball was stationary at the instant when it was hit. The mass of the tennis ball is 5.8 × 10–2 kg. The area under the curve is 0.84 N s.
(a) Calculate the speed of the ball as it leaves the racket. [2]
(b) Show that the average force exerted on the ball by the racket is about 50 N. [2]
(c) Determine, with reference to the work done by the average force, the horizontal distance travelled by the ball while it was in contact with the racket. [3]
(d) Draw a graph to show the variation with t of the horizontal speed v of the ball while it was in contact with the racket. Numbers are not required on the axes. [2]
▶️Answer/Explanation
Ans:
a
links 0.84 to ∆p
v = « \(\frac{0.84}{5.8\times 10^{-2}}\)»14.5 «ms-1»
b
use of ∆t = « (28 – 12) × 10 -3 « s»
F = « \(\frac{\Delta p}{\Delta t}\)= » \(\frac{0.84}{16\times 10^{-3}}\) OR 53 « N »
c
EK = \(\frac{1}{2}\) × 5.8 ×10-2 ×14.52
EK = W
S = « \(\frac{W}{F}\) = \(\frac{\frac{1}{2}\times 5.8\times 10^{-2}\times 14.5^2}{53}\) = » 0.12 «m»
d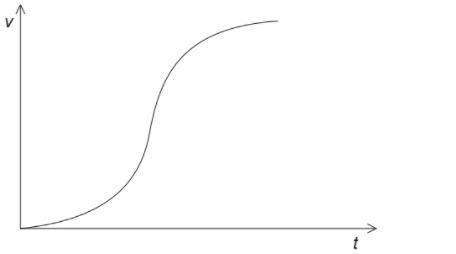 
graph must show increasing speed from an initial of zero all the time overall correct curvature
Question
A football player kicks a stationary ball of mass 0.45 kg towards a wall. The initial speed of the ball after the kick is 19 m 
and the ball does not rotate. Air resistance is negligible and there is no wind.
(a) The player’s foot is in contact with the ball for 55 ms. Calculate the average force that acts on the ball due to the football player. [2]
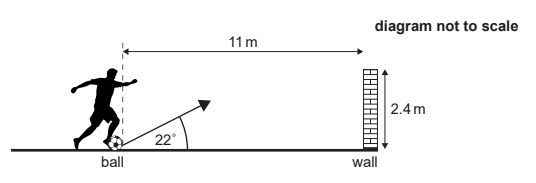
(b) (i) The ball leaves the ground at an angle of 22°. The horizontal distance from the initial position of the edge of the ball to the wall is 11 m. Calculate the time taken for the ball to reach the wall. [2]
(ii) The top of the wall is 2.4 m above the ground. Deduce whether the ball will hit the wall. [3]
(c) In practice, air resistance affects the ball. Outline the effect that air resistance has on the vertical acceleration of the ball. Take the direction of the acceleration due to gravity to be positive. [2]
▶️Answer/Explanation
Ans:
a ∆p × 0.45 19 OR a = «=
»160 «N» Allow [2] marks for a bald correct answer. Allow ECF for MP2 if 19 sin22 OR 19 cos22 used.
b i horizontal speed = 19 x cos 22 «= 17.6 m s-1 » time = « » 0.62 «s»
b ii initial vertical speed = 19 x sin 22 «= 7.1 m s-1 » «7.12 x 0.624 – 0.5 x 9.81 x 0.6242 =» 2.5 «m» ball does not hit wall OR 2.5 m 2.4 m « » > « » Allow ECF from (b)(i) and from MP1 Allow g = 10 m s-2 3 1.
c air resistance opposes «direction of» motion OR air resistance opposes velocity on the way up «vertical» acceleration is increased OR greater than g on the way down «vertical» acceleration is decreased OR smaller than g Allow deceleration/acceleration but meaning must be clear
Related Links