IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.1 – Motion
Topic 2 Weightage : 13 %
All Questions for Topic 2.1 – Distance and displacement , Speed and velocity , Acceleration , Graphs describing motion , Equations of motion for uniform acceleration , Projectile motion , Fluid resistance and terminal speed
Question
Two players are playing table tennis. Player A hits the ball at a height of 0.24 m above the edge of the table, measured from the top of the table to the bottom of the ball. The initial speed of the ball is 12.0 m s-1 horizontally. Assume that air resistance is negligible.
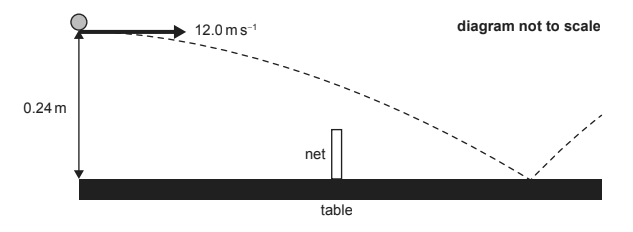
(a) Show that the time taken for the ball to reach the surface of the table is about 0.2 s. [1]
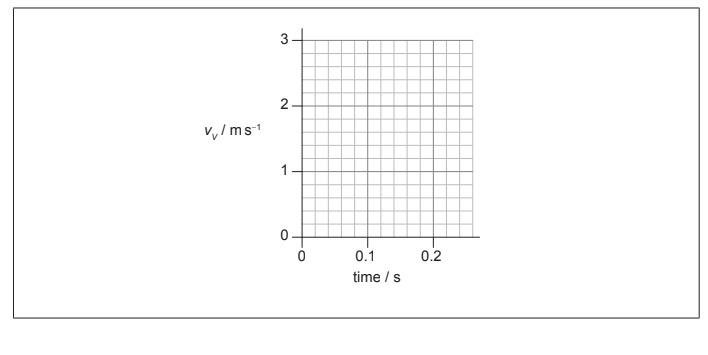
(b) Sketch, on the axes, a graph showing the variation with time of the vertical component of velocity vv of the ball until it reaches the table surface. Take g to be +10 m s-2 . [2]
(c) The net is stretched across the middle of the table. The table has a length of 2.74 m and the net has a height of 15.0 cm. Show that the ball will go over the net. [3]
(d) The ball bounces and then reaches a peak height of 0.18 m above the table with a horizontal speed of 10.5 m s-1. The mass of the ball is 2.7 g.
(i) Determine the kinetic energy of the ball immediately after the bounce. [2]
(ii) Player B intercepts the ball when it is at its peak height. Player B holds a paddle (racket) stationary and vertical. The ball is in contact with the paddle for 0.010 s.
Assume the collision is elastic.
Calculate the average force exerted by the ball on the paddle. State your answer to an appropriate number of significant figures. [3]
▶️Answer/Explanation
Ans:
a t = « \(\sqrt{\frac{2d}{g}}\) = »0.22 «s » OR t= \(\sqrt{\frac{2\times0.24}{9.8}}\) Answer to 2 or more significant figures or formula with variables replaced by correct values.
b increasing straight line from zero up to 0.2 s in x-axis √ with gradient = 10
c t= \(\frac{1.37}{12}\) = «0.114 s» y = \(\frac{1}{2}\) × 10 × 0.1142so (0.24-0.065) = 0.175>0.15 OR 0.065 < (0.24-0.15) «so it goes over the net» ALTERNATIVE« 2 0.24 0.15 0.09 = so» t s = 0.134 √ 0.134 12 1.6m × = 1.6 1.37 > «so ball passed the net already»
d i ALTERNATIVE 1 KE=
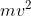+ mgh = 0.0027 × 10.
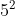+0.0027 + 9.8 0.18 √ 0.15 «J» ALTERNATIVE 2 Use of vx = 10.5AND vy = 1.88 to get » V = « \(\sqrt{10.5a^{2}+ 1.88a^{2}}\) = » 10.67 m s−1 = » KE= 
× 0.0027 ×10.672 0.15 «J »
d.ii v 21 m s−1 ∆ = » F= \(\frac{0.0027\times 21 }{0.01}\) OR 5.67 «N» any answer to 2 significant figures «N»
Question
A company delivers packages to customers using a small unmanned aircraft. Rotating horizontal blades exert a force on the surrounding air. The air above the aircraft is initially stationary.
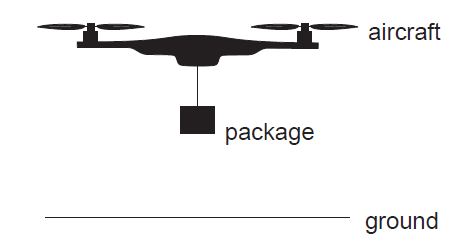
The air is propelled vertically downwards with speed v. The aircraft hovers motionless above the ground. A package is suspended from the aircraft on a string. The mass of the aircraft is
0.95 kg and the combined mass of the package and string is 0.45 kg. The mass of air pushed downwards by the blades in one second is 1.7 kg.
(a) State the value of the resultant force on the aircraft when hovering. [1]
(b)Outline, by reference to Newton’s third law, how the upward lift force on the aircraft is achieved. [2]
(c)Determine ν. State your answer to an appropriate number of significant figures. [3]
(d) The package and string are now released and fall to the ground. The lift force on the aircraft remains unchanged. Calculate the initial acceleration of the aircraft. [2]
▶️Answer/Explanation
Ans
(a) Ans : zero ✓
(b)
Blades exert a downward force on the air ✓
air exerts an equal and opposite force on the blades «by Newton’s third law» OR
air exerts a reaction force on the blades «by Newton’s third law» ✓
(c)
«lift force/change of momentum in one second» = 1.7 v
1.7 v = (0.95 + 0.45) X 9.81
v = 8.1 “ ms-1 ” AND answer expressed to 2 sf only
Allow 8.2 from g = 10 ms –2
(d)
vertical force = lift force – weight OR = 0.45 x 9.81 OR = 4.4 ” N ”
acceleration = (0.45 * 9.81)/0.95 =4.6 m s-2
In 1997 a high-speed car of mass \(1.1 \times {10^4}{\text{ kg}}\) achieved the world land speed record. The car accelerated uniformly in two stages as shown in the table. The car started from rest.
Use the data to calculate the
a. average acceleration of the car in stage 1. [1]
▶️Answer/Explanation
Markscheme
a. \(11{\text{ m}}{{\text{s}}^{ – 2}}\);
\(\Delta v = 236\);
\(a = \left( {\frac{{236}}{8} = } \right){\text{ }}29.5{\text{ }}\left( {{\text{m}}\,{{\text{s}}^{ – 2}}} \right)\);
\((F = 1.1 \times {10^4} \times 29.5) = 3.2 \times {10^5}{\text{ N}}\);
Award [2 max] for omission of initial speed (answer is 390 kN).
Award [3] for correct bald answer.
total 1400 m;
Award [2] for correct bald answer.
Watch for significant figure penalty in this question (1384 m).
Award [1 max] for \(\frac{1}{2}\)at2 substituted correctly for first phase, if no distances
evaluated and answer incorrect.
Award [1 max] for correct addition of incorrect phase 1 and/or 2 distance(s).