IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 3.1 – Thermal Concepts
Topic 3 Weightage : 3 %
All Questions for Topic 3.1 –Molecular theory of solids, liquids and gases , Temperature and absolute temperature , Internal energy , Specific heat capacity , Phase change , Specific latent heat
Question
A container with 0.60kg of a liquid substance is placed on a heater at time t=0. The specific latent heat of vaporization of the substance is 200kJkg–1. The graph shows the variation of the temperature T of the substance with time t.
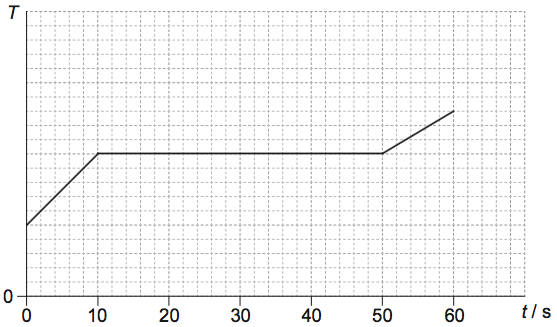
What is the power of the heater?
A. 1200 W
B. 3000 W
C. 4800 W
D. 13 300 W
▶️Answer/Explanation
Markscheme
B
We know \(Power =P=\frac{\Delta W}{\Delta t}\)
Now \(\Delta W =mL= 0.6 \times 200 \times 10^3\)
and \(\Delta t = (50-10) =40 s\)
Hence \(\Delta P=\frac{0.6 \times 200 \times 10^3}{40} =3000W\)
Question
An insulated tube is filled with a large number n of lead spheres, each of mass m. The tube is inverted s times so that the spheres completely fall through an average distance L each time. The temperature of the spheres is measured before and after the inversions and the resultant change in temperature is ΔT.
What is the specific heat capacity of lead?
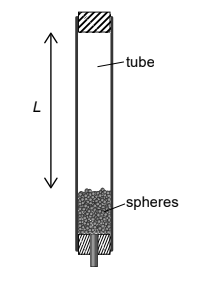
A \(\frac{sgL}{nm\Delta T}\)
B \(\frac{sgL}{\Delta T}\)
C \(\frac{sgL}{n\Delta T}\)
D \(\frac{gL}{m\Delta T}\)
▶️Answer/Explanation
Ans: B
Here Mechanical energy is converted into Heat Energy.
Each Sphere is moved through a distance of L . hence Gravitation field energy for each sphere each time of inversion = \(mgL\)
Now there are \(n\) sphere which are inverted \(s\) number of times . Hence mechanical (gravitation energy) = \(nsmgL\)
Now \(n\) sphere temperature raise by \(\Delta T\) times. Let \(c\) be specific heat capacity of lead
Hence total heat energy required to raise temperature by \(\Delta T\) = \(nmc\Delta T\)
Hence
\(nmc\Delta T = nsmgL\)
or
\(c=\frac{nsmgL}{nm\Delta T}=\frac{sgL}{\Delta T}\)
Question
A mass m of water is at a temperature of 290 K. The specific heat capacity of water is c . Ice, at its melting point, is added to the water to reduce the water temperature to the freezing point. The specific latent heat of fusion for ice is L . What is the minimum mass of ice that is required?
A \(\frac{17mc}{L}\)
B \(\frac{290mc}{L}\)
C \(\frac{17mL}{c}\)
D \(\frac{290mL}{c}\)
Answer/Explanation
Ans: A
Heat loss by water to loose temperature from 290 K to 273 K ( Melting point of water) is used by ice to melt.
hence applying heat loss = heat gain
\(mc(290-273)={m}’L\)
or
\(17mc={m}’L\)
or
\({m}’=\frac{17mc}{L}\)
