IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 4.2 – Travelling Waves
Topic 4 Weightage : 10 %
All Questions for Topic 4.2 – Travelling waves , Wavelength, frequency, period and wave speed , Transverse and longitudinal waves , The nature of electromagnetic waves , The nature of sound waves
Question
Two loudspeakers, A and B, are driven in phase and with the same amplitude at a frequency of 850 Hz. Point P is located 22.5 m from A and 24.3 m from B. The speed of sound is 340 m s–1.

a. Deduce that a minimum intensity of sound is heard at P.
A microphone moves along the line from P to Q. PQ is normal to the line midway between the loudspeakers.

b. The intensity of sound is detected by the microphone. Predict the variation of detected intensity as the microphone moves from P to Q.
c. When both loudspeakers are operating, the intensity of sound recorded at Q is I0. Loudspeaker B is now disconnected. Loudspeaker A continues to emit sound with unchanged amplitude and frequency. The intensity of sound recorded at Q changes to IA. Estimate Io /IA
▶️Answer/Explanation
Ans:
a.
wavelength = 340/850 = 0.40 m
path difference = 1.8 «m» 1.8 «m» = 4.5 λ OR 1.8/0.20 =9 = «half-wavelengths»
waves meet in antiphase «at P» OR destructive interference/superposition «at P»
b. «equally spaced» maxima and minima ✓
a maximum at Q ✓
four «additional» maxima «between P and Q»
c. the amplitude of sound at Q is halved ✓
«intensity is proportional to amplitude squared hence»
IA/Io = 1/4
Question
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
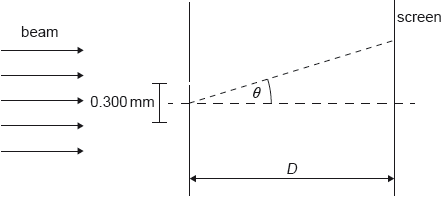
The air between the slits and the screen is replaced with water. The refractive index of water is 1.33.
a.i.
A series of dark and bright fringes appears on the screen. Explain how a dark fringe is formed.[3]
The wavelength of the beam as observed on Earth is 633.0 nm. The separation between a dark and a bright fringe on the screen is 4.50 mm. Calculate D.[2]
Calculate the wavelength of the light in water.[1]
State two ways in which the intensity pattern on the screen changes.[2]
▶️Answer/Explanation
Markscheme
a.i.
superposition of light from each slit / interference of light from both slits
with path/phase difference of any half-odd multiple of wavelength/any odd multiple of \(\pi \) (in words or symbols)
producing destructive interference
Ignore any reference to crests and troughs.[3 marks]
evidence of solving for D «D = \(\frac{{sd}}{\lambda }\)»
«\(\frac{{4.50 \times {{10}^{ – 3}} \times 0.300 \times {{10}^{ – 3}}}}{{633.0 \times {{10}^{ – 9}}}}\) × 2» = 4.27 «m»
Award [1] max for 2.13 m.[2 marks]
\(\frac{{633.0}}{{1.33}}\) = 476 «nm»[1 mark]
distance between peaks decreases
intensity decreases[2 marks]
Question
A longitudinal wave is travelling in a medium from left to right. The graph shows the variation with distance x of the displacement y of the particles in the medium. The solid line and the dotted line show the displacement at t=0 and t=0.882 ms, respectively.
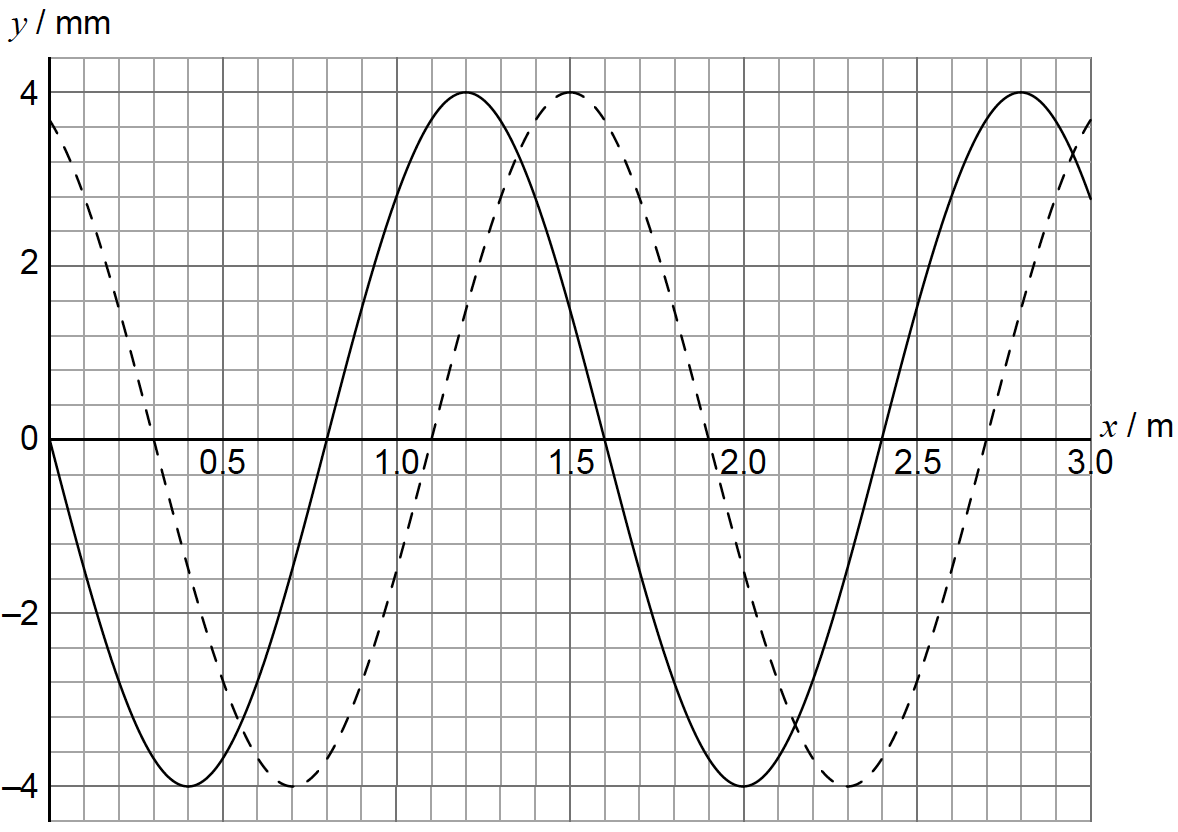
The period of the wave is greater than 0.882 ms. A displacement to the right of the equilibrium position is positive.
a.
State what is meant by a longitudinal travelling wave.[1]
Calculate, for this wave,
(i) the speed.
(ii) the frequency.[4]
The equilibrium position of a particle in the medium is at x=0.80 m. For this particle at t=0, state and explain
(i) the direction of motion.
(ii) whether the particle is at the centre of a compression or a rarefaction.[4]
▶️Answer/Explanation
Markscheme
a.
a wave where the displacement of particles/oscillations of particles/movement of particles/vibrations of particles is parallel to the direction of energy transfer/wave travel/wave movement
Do not allow “direction of wave”.
(i)
ALTERNATIVE 1
«distance travelled by wave =» 0.30 m
\(v = \ll \frac{{{\rm{distance}}}}{{{\rm{time}}}} = \gg 340{\rm{m}}{{\rm{s}}^{ – 1}}\)
ALTERNATIVE 2
evaluates \(T = \frac{{{\rm{0.882}} \times {{10}^{ – 3}} \times 1.6}}{{{\rm{0.3}}}}\)«=4.7ms» to give f = 210 or 212 Hz
uses λ=1.6 m with v=fλ to give 340ms–1
(ii)
ALTERNATIVE 1
λ=1.60m
f=\(\frac{{340}}{{1.60}}\)=212 or 213Hz
ALTERNATIVE 2
\(T = \frac{{0.882 \times {{10}^{ – 3}} \times 1.6}}{{0.3}}\)«=4.7ms»
\(F = \ll \frac{1}{T} = \gg {\rm{ 210Hz}}\)
(i)
the displacement of the particle decreases OR «on the graph» displacement is going in a negative direction OR on the graph the particle goes down
to the left
Do not allow “moving downwards” unless accompanied by reference to graph.
(ii)
molecules to the left of the particle have moved left and those to the right have moved right
«hence» the particle is at the centre of a rarefaction
