IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 5.3 Electric cells
Topic 5 Weightage : 5 %
All Questions for Topic 5.3 – Cells , Internal resistance , Secondary cells , Terminal potential difference , Electromotive force (emf)
Question
A girl rides a bicycle that is powered by an electric motor. A battery transfers energy to the electric motor.
The emf of the battery is 16 V and it can deliver a charge of 43 kC when discharging completely from a full charge.
(a) The maximum speed of the girl on a horizontal road is 7.0 m s–1 with energy from the battery alone.
The maximum distance that the girl can travel under these conditions is 20 km.
(i) Show that the time taken for the battery to discharge is about 3 ×103 s. [1]
(ii) Deduce that the average power output of the battery is about 240 W. [2]
(iii) Friction and air resistance act on the bicycle and the girl when they move.
Assume that all the energy is transferred from the battery to the electric motor.
Determine the total average resistive force that acts on the bicycle and the girl. [2]
(b) The bicycle and the girl have a total mass of 66 kg. The girl rides up a slope that is at an angle of 3.0° to the horizontal.
(i) Calculate the component of weight for the bicycle and girl acting down the slope. [1]
(ii) The battery continues to give an output power of 240 W. Assume that the resistive forces are the same as in (a)(iii).
Calculate the maximum speed of the bicycle and the girl up the slope. [2]
(c) On another journey up the slope, the girl carries an additional mass. Explain whether carrying this mass will change the maximum distance that the bicycle can travel along the slope. [2]
(d) The bicycle has a meter that displays the current and the terminal potential difference (pd) for the battery when the motor is running. The diagram shows the meter readings at one instant. The emf of the cell is 16 V.
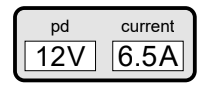
Determine the internal resistance of the battery. [2]
(e) The battery is made from an arrangement of 10 identical cells as shown.
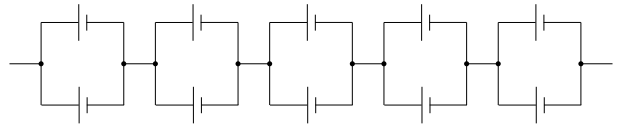
Calculate
(i) the emf of one cell. [1]
(ii) the internal resistance of one cell. [2]
▶️Answer/Explanation
Ans:
a i time taken \(\frac{2.0\times 10^4}{7}\) «= 2860 s» = 2900«s»
a ii
use of E = qV OR energy = 4.3 × 104 × 16 « = 6.88 × 105 «J »
power = 241 «W»
Accept 229 W – 241 W depending on the exact value of t used from ai. Must see at least three s.f.
a iii
use of power = force x speed OR force x distance = power x time
34 «N »
Accept 34 N – 36 N.
b i 66g sin(3°) = 34 «N»
b ii
total force 34 + 34 = 68 «N»
3.5 «ms-1»
c
«maximum» distance will decrease OWTTE ✔
because opposing/resistive force has increased
OR
because more energy is transferred to GPE
OR
because velocity has decreased
OR
increased mass means more work required «to move up the hill» ✔
d
4V dropped across battery OR Rcircuit = 1.85 Ω
so internal resistance = \(\frac{4.0}{6.5}\)= 0.62 «Ω»
e i \(\frac{16}{5}\) 3.2 = «V»
e ii
ALTERNATIVE
1: 2.5r = 0.62 r = 0.25 «Ω»
ALTERNATIVE 2:
\(\frac{0.62}{5}\) = 0.124 «Ω»
r = 2(0.124)= 0.248 «Ω»
This question is about a thermistor circuit.
The circuit shows a negative temperature coefficient (NTC) thermistor X and a 100 kΩ fixed resistor R connected across a battery.
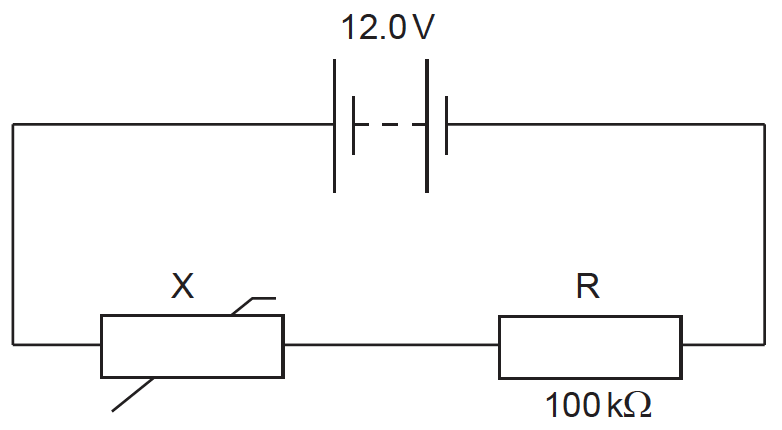
The battery has an electromotive force (emf) of 12.0 V and negligible internal resistance.
a.
Define electromotive force (emf).[1]
The graph below shows the variation with temperature T of the resistance RX of the thermistor.
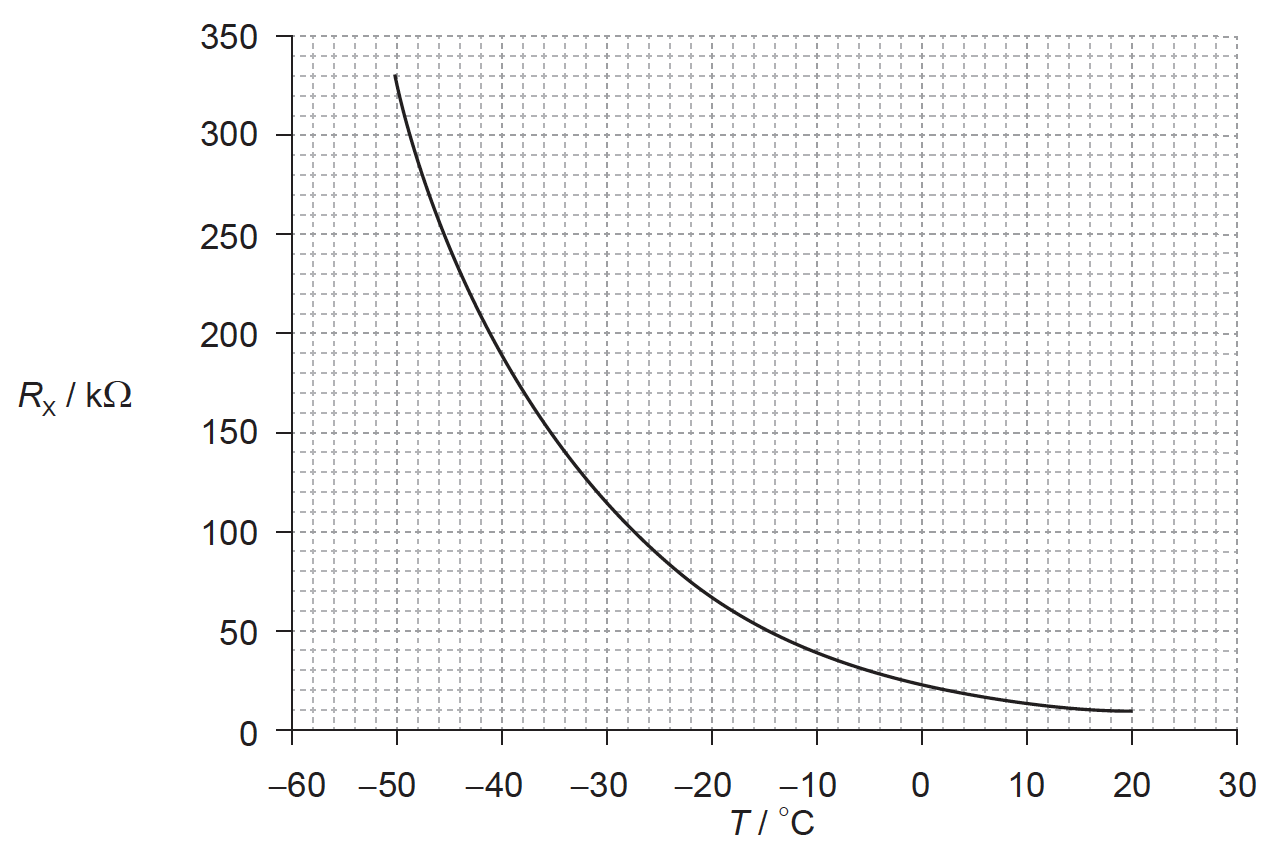
(i) Determine the temperature of X when the potential difference across R is 4.5 V.
(ii) State the range of temperatures for which the change in the resistance of the thermistor is most sensitive to changes in temperature.
(iii) State and explain the effect of a decrease in temperature on the ratio \(\frac{{{\rm{voltage across X}}}}{{{\rm{voltage across R}}}}\).[7]
▶️Answer/Explanation
Markscheme
a.
the work done per unit charge in moving a quantity of charge completely around a circuit / the power delivered per unit current / work done per unit charge made available by a source;
This question is in two parts. Part 1 is about electrical circuits. Part 2 is about magnetic
fields.
Part 1 Electrical circuits
The circuit shown is used to investigate how the power developed by a cell varies when the
load resistance \(R\) changes.
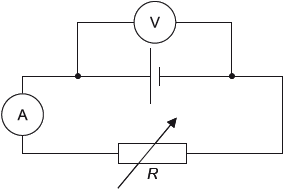
The variable resistor is adjusted and a series of current and voltage readings are taken.
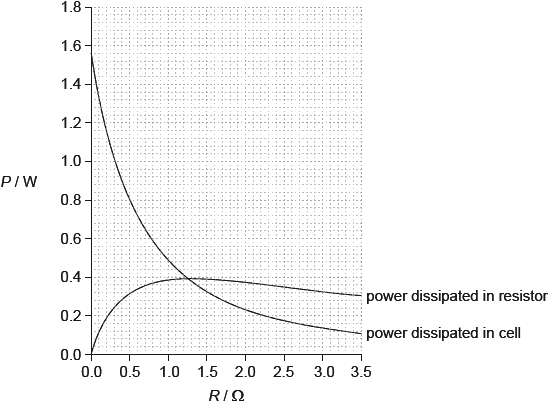
The graph shows the variation with \(R\) of the power dissipated in the cell and the power
dissipated in the variable resistor.
This question is in two parts. Part 1 is about electrical circuits. Part 2 is about magnetic
fields.
Part 2 Magnetic fields
The diagram shows an arrangement for measuring the force between two parallel sections of the same rigid wire carrying a current as viewed from the front.
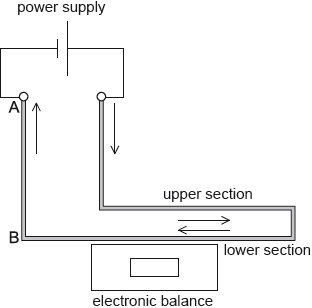
The supports for the upper section of the wire and the power supply are not shown.
When the current in the wire is 0.20 A, the magnetic field strength at the upper section of wire due to the lower section of wire is \(1.3 \times {10^{ – 4}}{\text{ T}}\).
d. The cell may be damaged if it dissipates a power greater than 1.2 W. Outline why damage in the cell may occur if the terminals of the cell are short-circuited.[2]
Using the diagram, draw the magnetic field pattern due to just the current in wire AB.[2]
▶️Answer/Explanation
Markscheme
d.
in this case \(R = 0\) / total resistance is internal resistance;
power dissipated is greater than 1.2 W / power dissipated is 1.56 (W) which is larger than limit; } (must be quantitative not “it’s too big”)
minimum of two concentric circles;
three circles, centered on wire with separation increasing with distance from the wire;
minimum of one arrow showing anticlockwise;
magnetic field due to upper wire on lower wire horizontal and into page;
shows force is downwards by any valid rule; (allow ECF from “out of page”)
reading of balance increases; (allow ECF)
or
currents are antiparallel / in opposite directions;
so wires repelled (by any argument giving force direction);
reading of balance increases;
\(2.6 \times {10^{ – 5}}{\text{ (N}}{{\text{m}}^{ – 1}})\);
volume of wire \( = \pi \times \frac{{{{\left( {2.5 \times {{10}^{ – 3}}} \right)}^2}}}{4} \times 0.15{\text{ }}( = 7.36 \times {10^{ – 7}}{\text{ }}{{\text{m}}^3})\);
charge in wire \( = 8.5 \times {10^{28}} \times 7.36 \times {10^{ – 7}} \times 1.6 \times {10^{ – 19}}{\text{ }}( = 10 \times {10^3}{\text{ C)}}\);
\(v = \frac{F}{{Bq}} = \frac{{3.9 \times {{10}^{ – 6}}}}{{1.3 \times {{10}^{ – 4}} \times {{10}^4}}}\);
\(3.0{\text{ }}\mu {\text{m}}\,{{\text{s}}^{ – 1}}\); (allow ECF from (g)(i))
N.B.: answer should be 0.115 \( \times \) their (g)(i).
Confusing diameter with radius gives answer of 0.75 \(\mu m\,\)s–1 – award [3 max].
Award [4] for a bald correct answer.
parts of the wire will experience a smaller magnetic field;
and hence a smaller force;
so the reading of the balance will decrease / OWTTE;
