IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 5.3 – Electric Cells
Topic 5 Weightage : 8 %
All Questions for Topic 5.3 – Cells , Internal resistance , Secondary cells , Terminal potential difference , Electromotive force (emf)
This question is in two parts. Part 1 is about kinematics and Newton’s laws of motion.
Part 2 is about electrical circuits.
Part 1 Kinematics and Newton’s laws of motion
Cars I and B are on a straight race track. I is moving at a constant speed of \({\text{45 m}}\,{{\text{s}}^{ – 1}}\) and B is initially at rest. As I passes B, B starts to move with an acceleration of \({\text{3.2 m}}\,{{\text{s}}^{ – 2}}\).
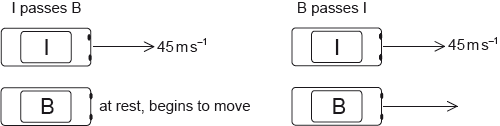
At a later time B passes I. You may assume that both cars are point particles.
A third car O with mass 930 kg joins the race. O collides with I from behind, moving along the same straight line as I. Before the collision the speed of I is \({\text{45 m}}\,{{\text{s}}^{ – 1}}\) and its mass is 850 kg. After the collision, I and O stick together and move in a straight line with an initial combined speed of \({\text{52 m}}\,{{\text{s}}^{ – 1}}\).
This question is in two parts. Part 1 is about kinematics and Newton’s laws of motion.
Part 2 Electrical circuits
The circuit shown is used to investigate how the power developed by a cell varies when the load resistance \(R\) changes.
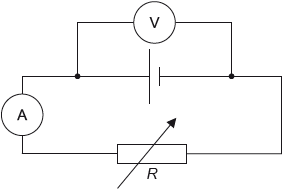
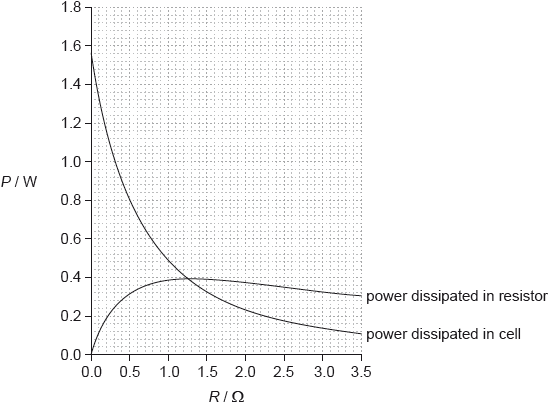
The variable resistor is adjusted and a series of current and voltage readings are taken. The graph shows the variation with \(R\) of the power dissipated in the cell and the power dissipated in the variable resistor.
The cell has an internal resistance.
a.i. Show that the time taken for B to pass I is approximately 28 s. [4]
▶️Answer/Explanation
Markscheme
a.i. distances itemized; (it must be clear through use of \({s_I}\) or distance I etc)
distances equated;
\(t = \frac{{2v}}{a}\) / cancel and re-arrange;
substitution \(\left( {\frac{{2 \times 45}}{{3.2}}} \right)\) shown / 28.1(s) seen;
or
clear written statement that the average speed of B must be the same as constant speed of I;
as B starts from rest the final speed must be \({\text{2}} \times {\text{45}}\);
so \(t = \frac{{\Delta v}}{a} = \frac{{90}}{{3.2}}\);
28.1 (s) seen; (for this alternative the method must be clearly described)
or
attempts to compare distance travelled by I and B for 28 s;
I distance \( = (45 \times 28 = ){\text{ }}1260{\text{ (m)}}\);
B distance \( = (\frac{1}{2} \times 3.2 \times {28^2} = ){\text{ }}1255{\text{ (m)}}\);
deduces that overtake must occur about \(\left( {\frac{5}{{45}} = } \right){\text{ }}0.1{\text{ s}}\) later;
\((1.26 \approx )\) 1.3 (km);
Award [2] for a bald correct answer.
driver B decelerating so (extra) force (to rear of car) (according to Newton 1) / momentum/inertia change so (extra) force must be present;
(hence) greater tension in belt B than belt I;
Award [0] for stating that tension is less in the decelerating car (B).
\(v = 58{\text{ }}({\text{m}}\,{{\text{s}}^{ – 1}})\);
Allow [2] for a bald correct answer.
\(13.2 \times {10^3}{\text{ (N)}}\); } (must see matched units and value ie: 13 200 without unit gains MP2, 13.2 does not)
Award [2] for a bald correct answer.
Allow use of 58 m s–1 from (c)(i) to give 12 400 (N).
voltmeter must have very large resistance/much larger than \(R\);
Allow [1 max] for zero and infinite resistance for ammeter and voltmeter respectively.
Allow [1 max] if superlative (eg: very/much/OWTTE) is missing.
\({I^2} \times 0.80 = 0.36\);
\(I = 0.67{\text{ (A)}}\) or \(\sqrt {\left( {\frac{{0.36}}{{0.8}}} \right)} \); (allow answers in the range of 0.66 to 0.68 (A).
leading to energy/power loss in the cell;
\({0.7^2} \times r = 0.58\);
\(r = 1.2{\text{ (}}\Omega {\text{)}}\); (allow answers in the range of 1.18 to 1.27 (\(\Omega \)))
or
when powers are equal;
\({I^2}R = {I^2}r\);
so \(r = R\) which occurs at 1.2(5) (\(\Omega \));
Award [1 max] for bald 1.2(5) (\(\Omega \)).
1.4 (V);
Allow ECF from (e) or (f)(ii).
or
when \(R = 0\), power loss \( = 1.55\);
\(E = (\sqrt {1.55 \times 1.2} = ){\text{ }}1.4{\text{ (V)}}\);
This question is about the internal resistance of a cell.
A circuit is used to determine the internal resistance and emf of a cell. It consists of the cell, a variable resistor, an ideal ammeter and an ideal voltmeter. The diagram shows part of the circuit with the ammeter and voltmeter missing.
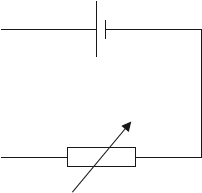
The variable resistor is set to \(1.5{\text{ }}\Omega \). When the cell converts 7.2 mJ of energy, 5.8 mC of charge moves completely around the circuit. The potential difference across the variable resistor is 0.55 V.
a. Define electromotive force (emf ).[1]
▶️Answer/Explanation
Markscheme
a. energy/work per unit charge supplied (by a cell) driving the current completely around a circuit;
quantity of chemical/any form of energy, per unit charge, changed to electrical energy;
potential difference across a cell when no current flows;
Allow similar responses.
Answer is given so award the mark for showing the working.
\((1.25 = 0.55 + Ir){\text{ }}r = 1.9{\text{ }}\Omega \); (accept valid alternative method)
0.20 W;
This question is in two parts. Part 1 is about the motion of a car. Part 2 is about electricity.
Part 1 Motion of a car
A car is travelling along the straight horizontal road at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\). The power output required at the wheels is 0.13 MW.
A driver moves the car in a horizontal circular path of radius 200 m. Each of the four tyres will not grip the road if the frictional force between a tyre and the road becomes less than 1500 N.
Part 2 Electricity
A lemon can be used to make an electric cell by pushing a copper rod and a zinc rod into the lemon.
A student constructs a lemon cell and connects it in an electrical circuit with a variable resistor. The student measures the potential difference V across the lemon and the current I in the lemon.
a. A car accelerates uniformly along a straight horizontal road from an initial speed of \({\text{12 m}}\,{{\text{s}}^{ – 1}}\) to a final speed of \({\text{28 m}}\,{{\text{s}}^{ – 1}}\) in a distance of 250 m. The mass of the car is 1200 kg. Determine the rate at which the engine is supplying kinetic energy to the car as it accelerates. [4]
(i) Calculate the total resistive force acting on the car when it is travelling at a constant speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\).
(ii) The mass of the car is 1200 kg. The resistive force \(F\) is related to the speed \(v\) by \(F \propto {v^2}\). Using your answer to (b)(i), determine the maximum theoretical acceleration of the car at a speed of \({\text{28 m}}\,{{\text{s}}^{ – 1}}\). [5]
(ii) While the car is travelling around the circle, the people in the car have the sensation that they are being thrown outwards. Outline how Newton’s first law of motion accounts for this sensation. [6]
(ii) Show that the potential difference \(V\) across the lemon is given by
\[V = E – Ir\]
where \(E\) is the emf of the lemon cell and \(r\) is the internal resistance of the lemon cell.
(iii) The graph shows how \(V\) varies with \(I\).
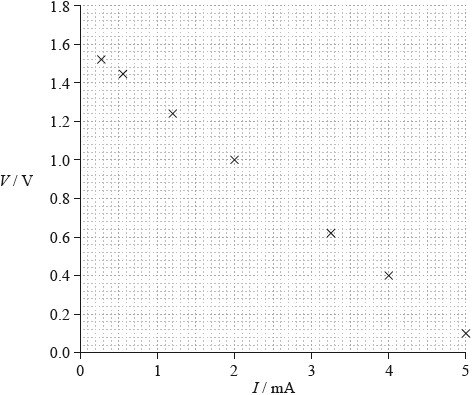
d. Using the graph, estimate the emf of the lemon cell.
(iv) Determine the internal resistance of the lemon cell.
(v) The lemon cell is used to supply energy to a digital clock that requires a current of \({\text{6.0 }}\mu {\text{A}}\). The clock runs for 16 hours. Calculate the charge that flows through the clock in this time.[10]
▶️Answer/Explanation
Markscheme
a. use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
change in kinetic energy \( = \frac{1}{2} \times 1200 \times \left[ {{{28}^2} – {{12}^2}} \right]{\text{ }}( = 384{\text{ kJ)}}\);
rate of change in kinetic energy \( = \frac{{384000}}{{12.5}}\); } (allow ECF of 162 from (28 – 12)2 for this mark)
31 (kW);
or
use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
use of a kinematic equation to determine acceleration \(( = {\text{1.28 m}}\,{{\text{s}}^{ – 2}}{\text{)}}\);
work done \( = \frac{{F \times s}}{{{\text{time}}}} = \frac{{1536 \times 250}}{{12.5}}\);
31 (kW);
(i) \({\text{force}} = \frac{{{\text{power}}}}{{{\text{speed}}}}\);
2300 or 2.3k (N);
Award [2] for a bald correct answer.
(ii) resistive force \( = \frac{{2300}}{4}\)\(\,\,\,\)or\(\,\,\,\)\(\frac{{2321}}{4}{\text{ }}( = 575)\); (allow ECF)
so accelerating force = \((2300 – 580 = ){\text{ }}1725{\text{ (N)}}\)\(\,\,\,\)or\(\,\,\,\)1741 (N);
\(a = \frac{{1725}}{{1200}} = 1.44{\text{ (m}}{{\text{s}}^{ – 2}}{\text{)}}\)\(\,\,\,\)or\(\,\,\,\)\(a = \frac{{1741}}{{1200}} = 1.45{\text{ (m}}\,{{\text{s}}^{ – 2}}{\text{)}}\);
Award [2 max] for an answer of 0.49 (m\(\,\)s–2) (omits 2300 N).
(i) centripetal force must be \( < {\text{6000 (N)}}\); (allow force = 6000 N)
\({v^2} = F \times \frac{r}{m}\);
\({\text{31.6 (m}}\,{{\text{s}}^{ – 1}}{\text{)}}\);
Allow [3] for a bald correct answer.
Allow [2 max] if 4\( \times \) is omitted, giving 15.8 (m\(\,\)s–1).
(ii) statement of Newton’s first law;
(hence) without car wall/restraint/friction at seat, the people in the car would move in a straight line/at a tangent to circle;
(hence) seat/seat belt/door exerts centripetal force;
(in frame of reference of the people) straight ahead movement is interpreted as “outwards”;
(i) voltmeter in parallel with cell; (allow ammeter within voltmeter leads)
ammeter in series with variable resistor; } (must draw as variable arrangement or as potential divider)
Allow cell symbol for lemon/cell/box labelled “lemon cell”.
Award [1 max] if additional cell appears in the circuit.
(ii) \(E = I(R + r)\) and \(V = IR\) used; (must state both explicitly)
re-arrangement correct ie \(E = V + Ir\); } (accept any other correct re-arrangement eg. involving energy conversion)
(iii) line correctly extrapolated to y-axis; (judge by eye)
1.6 or 1.60 (V); (allow ECF from incorrect extrapolation)
(iv) correct read-offs from large triangle greater than half line length;
gradient determined;
290 to 310 \({\text{(}}\Omega {\text{)}}\);
Award [2 max] for the use of one point on line and equation.
(v) 0.35 (C);
