IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 5.4 – Magnetic effect of electric currents
Topic 5 Weightage : 8 %
All Questions for Topic 5.4 – Magnetic fields , Magnetic force
Question
An electron moves in circular motion in a uniform magnetic field.
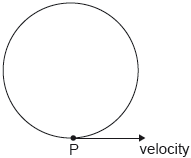
The velocity of the electron at point P is 6.8 × 105 m s–1 in the direction shown.
The magnitude of the magnetic field is 8.5 T.
a.State the direction of the magnetic field.[1]
▶️Answer/Explanation
Markscheme
a.
out of the page plane / ⊙
Do not accept just “up” or “outwards”.[1 mark]
OR
the magnetic force/acceleration is at right angles to velocity[1 mark]
(therefore) there is a centripetal acceleration / force acting on the charge
OWTTE[2 marks].
Question
In an experiment a student constructs the circuit shown in the diagram. The ammeter and the voltmeter are assumed to be ideal.
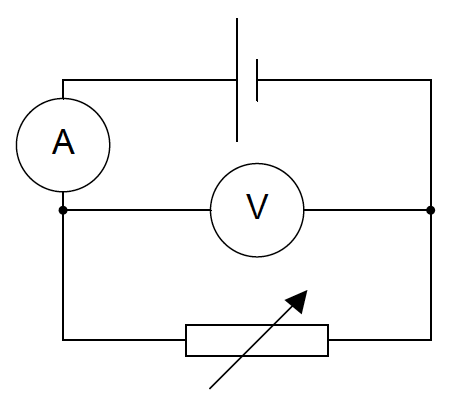
a.
State what is meant by an ideal voltmeter.[1]
The student adjusts the variable resistor and takes readings from the ammeter and voltmeter. The graph shows the variation of the voltmeter reading V with the ammeter reading I.
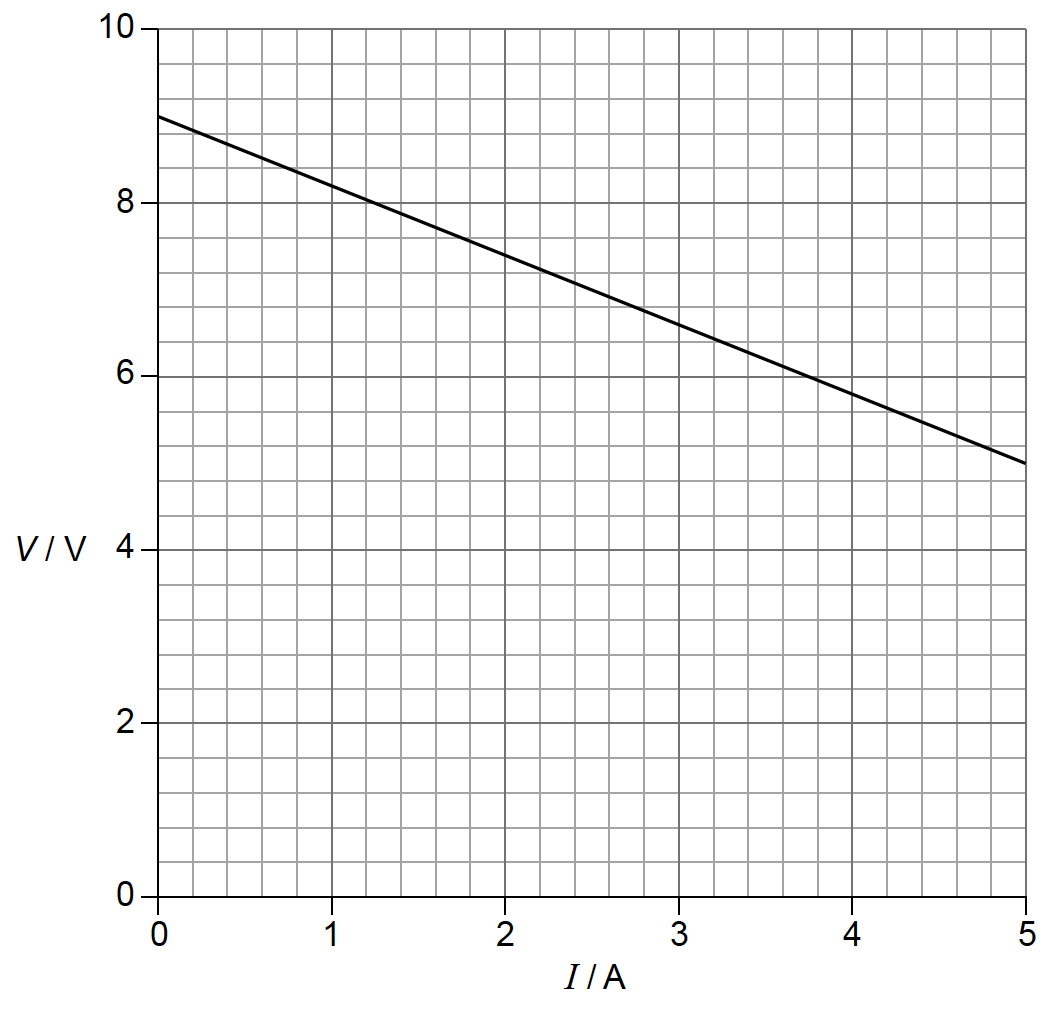
Use the graph to determine
(i) the electromotive force (emf) of the cell.
(ii) the internal resistance of the cell.[3]
A connecting wire in the circuit has a radius of 1.2mm and the current in it is 3.5A. The number of electrons per unit volume of the wire is 2.4×1028m−3. Show that the drift speed of the electrons in the wire is 2.0×10−4ms−1.[1]
The diagram shows a cross-sectional view of the connecting wire in (c).
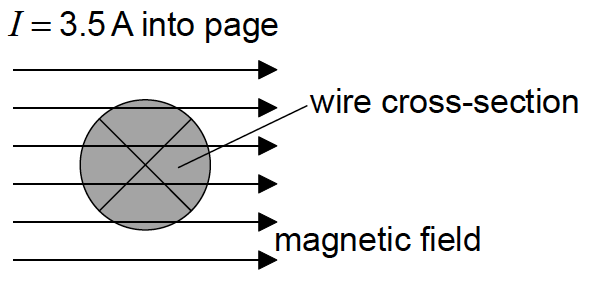
The wire which carries a current of 3.5A into the page, is placed in a region of uniform magnetic field of flux density 0.25T. The field is directed at right angles to the wire.
Determine the magnitude and direction of the magnetic force on one of the charge carriers in the wire.[2]
▶️Answer/Explanation
Markscheme
a.
infinite resistance OR draws no current from circuit/component OR has no effect on the circuit
Do not allow “very high resistance”.
(i)
«vertical intercept = emf» = 8.8 − 9.2 V
(ii)
attempt to evaluate gradient of graph
=0.80Ω
Accept other methods leading to correct answer, eg using individual data points from graph.
Allow a range of 0.78 – 0.82 Ω.
If ε = I(R + r) is used then the origin of the value for R must be clear.
3.5=2.4×1028×π(1.2×10−3)2×1.6×10−19×v«⇒v=2.0×10−4ms−1»
F = «qvB =1.6×10–19 ×2.0×10–4 ×0.25 =»8.1×10–24 N
directed down OR south
This question is about electric and magnetic fields.
A proton travelling to the right with horizontal speed 1.6×104ms–1 enters a uniform electric field of strength E. The electric field has magnitude 2.0×103NC–1 and is directed downwards.
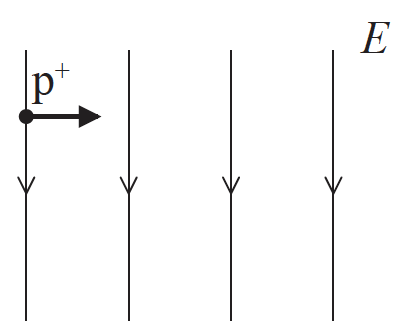
a.
Calculate the magnitude of the electric force acting on the proton when it is in the electric field.[2]
A uniform magnetic field is applied in the same region as the electric field. A second proton enters the field region with the same velocity as the proton in (a). This second proton continues to move horizontally.
(i) Determine the magnitude and direction of the magnetic field.
(ii) An alpha particle enters the field region at the same point as the second proton, moving with the same velocity. Explain whether or not the alpha particle will move in a straight line.[5]
▶️Answer/Explanation
Markscheme
=3.2×10-16(N);
(i) \(\left( {F = qvB \Rightarrow } \right)B = \frac{F}{{qv}}\) or \(\left( {Eq = qvB \Rightarrow } \right)B = \frac{E}{v}\);
\(\left( { = \frac{{3.2 \times {{10}^{ – 16}}}}{{1.6 \times {{10}^{ – 19}} \times 1.6 \times {{10}^4}}}} \right) = 0.13\) or 0.125(T);
directed into the page / OWTTE;
(ii) both electric and magnetic forces double / both forces increase by the same factor / both forces scale with q/charges and cancel;
so straight line followed; (only award if first mark awarded)
or
straight line followed if qE = qvB ⇒E v=B;
E, v and B constant (so straight line followed);
