IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 6.2 Newton’s law of gravitation
Topic 6 Weightage : 1 %
All Questions for Topic 6.2 – Newton’s law of gravitation , Gravitational field strength
A planet has radius R. At a distance h above the surface of the planet the gravitational field strength is g and the gravitational potential is V.
a.i. State what is meant by gravitational field strength.[1]
[2]
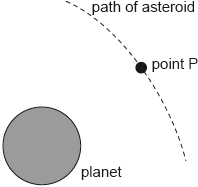
When the asteroid was far away from the planet it had negligible speed. Estimate the speed of the asteroid at point P as defined in (b).[3]
▶️Answer/Explanation
Markscheme
a.i.
the «gravitational» force per unit mass exerted on a point/small/test mass[1 mark]
at height h potential is V = –\(\frac{{GM}}{{(R + h)}}\)
field is g = \(\frac{{GM}}{{{{(R + h)}^2}}}\)
«dividing gives answer»
Do not allow an answer that starts with g = –\(\frac{{\Delta V}}{{\Delta r}}\) and then cancels the deltas and substitutes R + h[2 marks]
correct shape and sign
non-zero negative vertical intercept
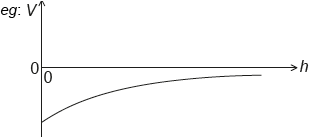[2 marks]
V = «–2.2 × (3.1 × 106 + 2.4 × 107) =» «–» 6.0 × 107 J kg–1
Unit is essential
Allow eg MJ kg–1 if power of 10 is correct
Allow other correct SI units eg m2s–2, N m kg–1[1 mark]
total energy at P = 0 / KE gained = GPE lost
«\(\frac{1}{2}\)mv2 + mV = 0 ⇒» v = \(\sqrt { – 2V} \)
v = «\(\sqrt {2 \times 6.0 \times {{10}^7}} \) =» 1.1 × 104 «ms–1»
Award [3] for a bald correct answer
Ignore negative sign errors in the workings
Allow ECF from 6(b)[3 marks]
ALTERNATIVE 1
force on asteroid is «6.2 × 1012 × 2.2 =» 1.4 × 1013 «N»
«by Newton’s third law» this is also the force on the planet
ALTERNATIVE 2
mass of planet = 2.4 x 1025 «kg» «from V = –\(\frac{{GM}}{{(R + h)}}\)»
force on planet «\(\frac{{GMm}}{{{{(R + h)}^2}}}\)» = 1.4 × 1013 «N»
MP2 must be explicit[2 marks]
The gravitational potential due to the Sun at its surface is –1.9 x 1011 J kg–1. The following data are available.
| Mass of Earth | = 6.0 x 1024 kg |
| Distance from Earth to Sun | = 1.5 x 1011 m |
| Radius of Sun | = 7.0 x 108 m |
a. Outline why the gravitational potential is negative.[2]
rVS = constant.[1]
▶️Answer/Explanation
Markscheme
a.
potential is defined to be zero at infinity
so a positive amount of work needs to be supplied for a mass to reach infinity
VS = \( – \frac{{GM}}{r}\) so r x VS «= –GM» = constant because G and M are constants
GM = 1.33 x 1020 «J m kg–1»
GPE at Earth orbit «= –\(\frac{{1.33 \times {{10}^{20}} \times 6.0 \times {{10}^{24}}}}{{1.5 \times {{10}^{11}}}}\)» = «–» 5.3 x 1033 «J»
Award [1 max] unless answer is to 2 sf.
Ignore addition of Sun radius to radius of Earth orbit.
ALTERNATIVE 1
work leading to statement that kinetic energy \(\frac{{GMm}}{{2r}}\), AND kinetic energy evaluated to be «+» 2.7 x 1033 «J»
energy «= PE + KE = answer to (b)(ii) + 2.7 x 1033» = «–» 2.7 x 1033 «J»
ALTERNATIVE 2
statement that kinetic energy is \( = – \frac{1}{2}\) gravitational potential energy in orbit
so energy «\( = \frac{{{\text{answer to (b)(ii)}}}}{2}\)» = «–» 2.7 x 1033 «J»
Various approaches possible.
«KE will initially decrease so» total energy decreases
OR
«KE will initially decrease so» total energy becomes more negative
Earth moves closer to Sun
new orbit with greater speed «but lower total energy»
changes ellipticity of orbit
centripetal force is required
and is provided by gravitational force between Earth and Sun
Award [1 max] for statement that there is a “centripetal force of gravity” without further qualification.
The diagram shows a planet near two stars of equal mass M.
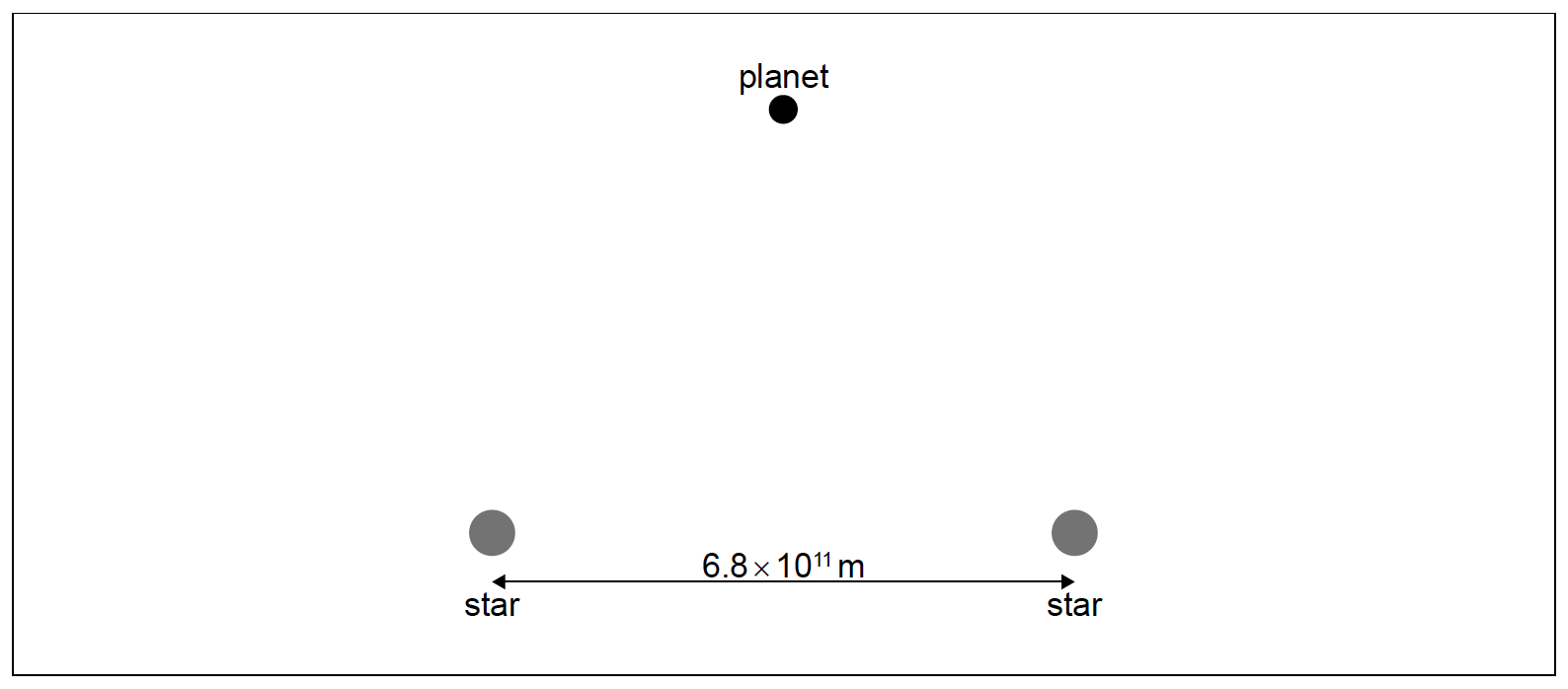
Each star has mass M=2.0×1030kg. Their centres are separated by a distance of 6.8×1011m. The planet is at a distance of 6.0×1011m from each star.
a. On the diagram above, draw two arrows to show the gravitational field strength at the position of the planet due to each of the stars.[2]
▶️Answer/Explanation
Markscheme
a.
two arrows each along the line connecting the planet to its star AND directed towards each star
arrow lines straight and of equal length
Do not allow kinked, fuzzy curved lines.
\(g = \ll \frac{{GM}}{{{r^2}}} = \frac{{6.67 \times {{10}^{ – 11}} \times 2.0 \times {{10}^{30}}}}{{{{\left( {6.0 \times {{10}^{11}}} \right)}^2}}} \gg \) OR 3.7×10-4Nkg-1
\({g_{{\rm{net}}}} = \ll 2g\cos \theta = 2 \times 3.7 \times {10^{ – 4}} \times \frac{{\sqrt {{{6.0}^2} – {{3.4}^2}} }}{{6.0}} = \gg 6.1 \times {10^{ – 4}}{\rm{Nk}}{{\rm{g}}^{ – 1}}\)
directed vertically down «page» OR towards midpoint between two stars OR south
Allow rounding errors.
Related Links