IBDP Physics 6.2 – Newton’s law of gravitation: IB Style Question Bank SL Paper 1

IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics

Topic 6.2 – Newton’s law of gravitation

Topic 6 Weightage : 4 %

All Questions for Topic 6.2 – Newton’s law of gravitation , Gravitational field strength

Question

Which is the definition of gravitational field strength at a point?

A The sum of the gravitational fields created by all masses around the point

B The gravitational force per unit mass experienced by a small point mass at that point

C G $\tfrac{M}{r^2}$ , where M is the mass of a planet and r is the distance from the planet to the point

D The resultant force of gravitational attraction on a mass at that point

▶️Answer/Explanation

Ans: B

The gravitational field strength Eg, produced by a mass M at any point P is defined as the force exerted on the unit mass placed at that point P. Then

…(i)

where m = test mass

r = distance between M and m

The direction of Eg always points towards the mass producing it.

The gravitational field can be represented by gravitational lines of force.

The S.I unit of Eg is newton/kg. Its dimensions are $M^0LT^{-2}$

Question

Newton’s law of gravitation

A. is equivalent to Newton’s second law of motion.

B. explains the origin of gravitation.

C. is used to make predictions.

D. is not valid in a vacuum.

▶️Answer/Explanation

Markscheme

Isaac Newton’s Law of Universal Gravitation is used to predict the position of planets based on their mutual force of gravity.

Question

The gravitational field strength at the surface of Earth is g. Another planet has double the radius of Earth and the same density as Earth. What is the gravitational field strength at the surface of this planet?

A. $\frac{g}{2}$

B. $\frac{g}{4}$

C. 2g

D. 4g

▶️Answer/Explanation

Markscheme

Gravitational field strength at earth , $g_e$

$= \frac{GM_e}{R^2} = \frac{G\times \frac{4}{3}\times \pi\times R_e^3\times \rho_e }{R_e^2}$

$= \frac{4}{3}\times G \times \pi\times \rho_e\times R_e$
Gravitational field strength at other planet , $ g_p$

$=\frac{4}{3}\times G \times \pi\times \rho_p\times R_p$
Now Given that

$R_p= 2\times R_e \; and \; \rho_e= \rho_p$
$\therefore \frac{g_p}{g_e} =$

$\frac{\frac{4}{3}\times G \times \pi\times \rho_p\times R_p}{\frac{4}{3}\times G \times \pi\times \rho_e\times R_e}$
$=\frac{2\times R_e}{R_e}=2$
$\therefore g_p = 2\times g_e$

Question

On Mars, the gravitational field strength is about $\frac{1}{4}$ of that on Earth. The mass of Earth is approximately ten times that of Mars.

What is $\frac{{{\text{radius of Earth}}}}{{{\text{radius of Mars}}}}$ ?

A. 0.4

B. 0.6

C. 1.6

D. 2.5

▶️Answer/Explanation

Markscheme

Gravitational field strength at Earth , $g_e$

$= \frac{GM_e}{R_e^2}$
Gravitational field strength at Mars $g_m = \frac{GM_m}{R_m^2}$
$\therefore \frac{g_m}{g_e}=\frac{\frac{GM_m}{R_m^2}}{\frac{GM_e}{R_e^2}}$
$=\frac{M_m \times R_e^2}{M_e \times R_m^2}$
Now given that $\frac {g_m}{g_e} =\frac{1}{4}$ and $ M_e = 10\ times M_m$
$\therefore \frac{M_m\times R_e^2}{10 \times M_m \times R_m^2} =\frac{1}{4}$
or
$\frac{R_e^2}{R_m^2} =\frac{10}{4}$
or
$\frac{R_e}{R_m}=\sqrt{2.5} =1.58 \approx 1.6$

Question

Which single condition enables Newton’s universal law of gravitation to be used to predict the force between the Earth and the Sun?

A. The Earth and the Sun both have a very large radius.

B. The distance between the Earth and the Sun is approximately constant.

C. The Earth and the Sun both have a very large mass.

D. The Earth and the Sun behave as point masses.

▶️Answer/Explanation

Markscheme

Although Newton’s law of gravitation applies strictly to particles, we can also apply it to real objects as long as the sizes of the objects are small relative to the distance between them.The Sun and Earth are far enough apart so that, to a good approximation, we can treat them both as particles

Question

A planet has half the mass and half the radius of the Earth. What is the gravitational field strength at the surface of the planet? The gravitational field strength at the surface of the Earth is 10 N kg^–1.

A. 2.5 N kg^–1

B. 5.0 N kg^–1

C. 10 N kg^–1

D. 20 N kg^–1

▶️Answer/Explanation

Markscheme

Gravitational field strength at Earth , $g_e$

$= \frac{GM_e}{R_e^2}$
Gravitational field strength at other planet $g_p = \frac{GM_p}{R_p^2}$
$\therefore \frac{g_p}{g_e}=\frac{\frac{GM_p}{R_m^2}}{\frac{GM_e}{R_e^2}}$
$=\frac{M_p \times R_e^2}{M_e \times R_p^2}$

Given that

$M_p=\frac{1}{2}M_e \; and \; R_p=\frac{1}{2} R_e$
Hence
$\frac{g_p}{g_e}=\frac{M_p \times R_e^2}{M_e \times R_p^2}$

$=\frac{\frac{1}{2}M_e \times R_e^2 }{M_e \times ({\frac{R_e}{2})}^{2}}=2$
$g_p= 2 \times g_e$
Now $ g_e = 10 \; Nkg^{-1}$
Hence $g_p = 2 \times 10 =20 \; Nkg^{-1}$

Question

A satellite X of mass m orbits the Earth with a period T. What will be the orbital period of satellite Y of mass 2m occupying the same orbit as X?

A. $\frac{T}{2}$

B. T

C. $\sqrt {2T} $

D. 2T

▶️Answer/Explanation

Markscheme

A satellite is any body revolving around a large body under the gravitational influence of the latter.

The period of motion T of an artificial satellite of earth at a distance h above the surface of the earth is given by,

where, $R_e$ = radius of the earth

where, g = acceleration due to gravity on the surface of the earth.

Here we can see Time period $T$ depends does not depends on Mass M , it depends on $g$ , $R_e$ and $h$ only . Hence both satellite will have same Time period which is $T$ as given in questions.

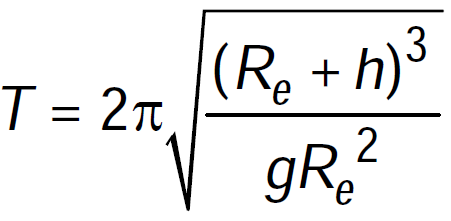
Question

Two satellites of mass m and 2m orbit a planet at the same orbit radius. If F is the force exerted on the satellite of mass m by the planet and a is the centripetal acceleration of this satellite, what is the force and acceleration of the satellite with mass 2m?

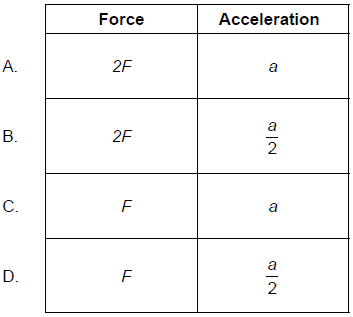
▶️Answer/Explanation

Markscheme

Let a satellite of mass m revolve around the earth in circular orbit of radius r with speed v0. The gravitational pull between satellite and earth provides the necessary centripetal force.

Centripetal force required for the motion =

By Newton’s second law, the force on the planet equals its mass times the acceleration. Thus,

Gravitational force = Centripetal force required for the motion = $\frac{GM_pm_s}{R_o^2}$

Where $M_p$ is mass of planet and $m_s$ is mass of satellite . Hence clearly if mass is doubled Force is doubled .

Now

$\frac{GM_pm_s}{R_o^2} = \frac{m_s v_0^2}{R_0}$

$\frac{GM_pm_s}{R_o^2}=\frac{m_s v_0^2}{R_0}$
or
$\frac{v_0^2}{R_0} =\frac{GM_p}{R_o^2}$

Here $\frac{v_0^2}{R_0} $ is independent of $m_s$ , mass of satellite and hence enen mass is doubled , acceleration remain constant.

Related Links

IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics

Question

Question

Markscheme

Question

Markscheme

Question

Markscheme

Question

Markscheme

Question

Markscheme

Question

Markscheme

Question

Markscheme

Need Help ? Book A Tutor