IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 7.2 – Nuclear reactions
Topic 7 Weightage : 7%
All Questions for Topic 7.2 – The unified atomic mass unit , Mass defect and nuclear binding energy , Nuclear fission and nuclear fusion
Question
What is the relation between the value of the unified atomic mass unit in grams and the value of Avogadro’s constant in 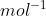 ?
?
A Their ratio is 1.
B Their product is 1.
C Their sum is 1.
D Their difference is 0.
▶️Answer/Explanation
Ans: B
unit which is widely used in describing mass in nuclear physics as well as in atomic physics is unified atomic mass unit denoted by the symbol \(u\). It is 1/12 of the mass of a neutral carbon atom in its lowest energy state which contains six protons, six neutrons and six electrons. We have
\(1u=1.66\times 10^{-27}kg= 931 MeVc^{-2}\)
Avogadro’s number is defined as the total number of atoms in \(12 g\) sample of \(carbon -12\)
so, \(12g \;_{}^{12}\textrm{C} \) contain \(N_A\) atoms
Therefore, 1 atom of carbon -12 weighs \(\frac{12}{N_A}g\)
As per the definition of atomic mass unit
\(1 amu = \frac{1}{12}\times \frac{12}{N_A}g\)
\(= \frac{1}{6.022 \times 10^{23}}g\)
Hence , \(1 amu = 1.6 \times 10^{-27}kg\)
Question
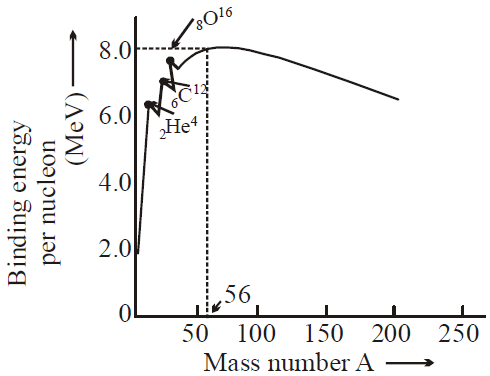
A graph of the variation of average binding energy per nucleon with nucleon number has a maximum. What is indicated by the region around the maximum?
A. The position below which radioactive decay cannot occur
B. The region in which fission is most likely to occur
C. The position where the most stable nuclides are found
D. The region in which fusion is most likely to occur
▶️Answer/Explanation
Markscheme
C
Question
The average binding energy per nucleon of the \(_8^{15}{\text{O}}\) nucleus is 7.5 MeV. What is the total energy required to separate the nucleons of one nucleus of \(_8^{15}{\text{O}}\)?
A. 53 MeV
B. 60 MeV
C. 113 MeV
D. 173 MeV
▶️Answer/Explanation
Markscheme
C
We can think of the binding energy per nucleon as the average energy needed to separate a nucleus into its individual nucleons. A greater binding energy per nucleon means a more tightly bound nucleus.
Binding Energy per Nucleon \(=\frac{Binding Energy}{Number of Nucleons}=\frac{B}{A}\)
\(B=Binding \; Energy \; per \; nucleon \times A\)
\(=7.5 \times 15\) Since \(A\) in \(_{8}^{15}\textrm{}O \) is \(A = 15\)
\(= 112.5 MeV\)
Question
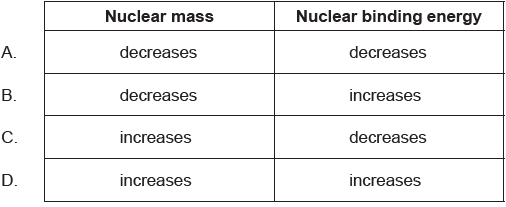
What gives the total change in nuclear mass and the change in nuclear binding energy as a result of a nuclear fusion reaction?
▶️Answer/Explanation
Markscheme
B
The mass M of a nucleus is less than the total mass ∑m of its individual protons and neutrons. That means that the mass energy \(Mc^2\) of a nucleus is less than the total mass energy \(\sum (mc^2)\) of its individual protons and neutrons. The difference between these two energies is called the binding energy of the nucleus:
\(\Delta E_{be} =\sum (mc^2)-Mc^2\)
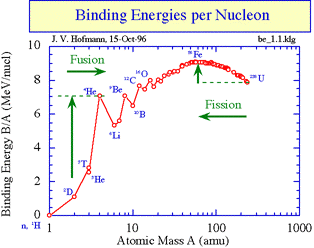
Energy is released when the binding energy per nucleon increases as this results in greater stability Nuclear reactions occur when the reactants have lower binding energy per nucleon than the products. If you look at the graph you can see that this can happen in two ways: if nuclei with very small values of A join together (fusion) they produce nuclei with larger values of A that have greater binding energy per nucleon,or large nuclei can split to form smaller nuclei (fission) that are higher up on the graph line (see arrows). Binding energy per nucleon increases by movement towards peak of graph.
Hence in a nuclear reaction Nuclear mass decreases and Binding Energy Increases.
Question
The binding energy per nucleon of \({}_4^{11}Be\) is 6 MeV. What is the energy required to separate the nucleons of this nucleus?
A. 24 MeV
B. 42 MeV
C. 66 MeV
D. 90 MeV
▶️Answer/Explanation
Markscheme
C
Binding energy per nucleon \(\Delta E_{ben}\), which is the ratio of the binding energy of a nucleus to the number A of nucleons in that nucleus:
\(\Delta E_{ben}=\frac{\Delta E_{be}}{A}\)
or
\(\Delta E_{be}=\Delta E_{ben} \times A\)
Given \(A= 11\) and \(\Delta E_{ben} = 6MeV\)
\(\therefore \Delta E_{be} = 6 \times 11 = 66\;MeV\)
Question
What is the energy equivalent to the mass of one proton?
A. 9.38 × (3 × 108)2 × 106 J
B. 9.38 × (3 × 108)2 × 1.6 × 10–19 J
C. \(\frac{{9.38 \times {{10}^8}}}{{1.6 \times {{10}^{ – 19}}}}\)J
D. 9.38 × 108 × 1.6 × 10–19 J
▶️Answer/Explanation
Markscheme
D
Energy Equivalent \(Q\) is given by \( Q = mc^2\)
Here m = m_p = 1.6 \times 10^{-19} and c= 3\times 10^8
Hence
\(Q= 1.66 \times 10^{-27} \times (3 \times 10^8)^{2}\)
\(Q= 1.66 \times 10^{-27} \times (3 \times 10^8)^{2} =9 \times 1.66\times 10^{-11}\)
same as value in D
Question
In nuclear fission, a nucleus of element X absorbs a neutron (n) to give a nucleus of element Y and a nucleus of element Z.
X + n → Y + Z + 2n
What is \(\frac{{{\text{magnitude of the binding energy per nucleon of Y}}}}{{{\text{magnitude of the binding energy per nucleon of X}}}}\) and \(\frac{{{\text{total binding energy of Y and Z}}}}{{{\text{total binding energy of X}}}}\)?
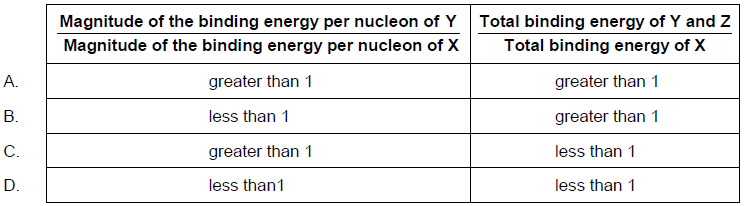
▶️Answer/Explanation
Markscheme
A

Energy is released when the binding energy per nucleon increases as this results in greater stability Nuclear reactions occur when the reactants have lower binding energy per nucleon than the products. If you look at the graph you can see that this can happen in two ways: if nuclei with very small values of A join together (fusion) they produce nuclei with larger values of A that have greater binding energy per nucleon,or large nuclei can split to form smaller nuclei (fission) that are higher up on the graph line (see arrows). Binding energy per nucleon increases by movement towards peak of graph.
Hence Binding energy of products are higher than reactant in case of Nuclear Fission reaction.
As mass of product combined together is less than mass of reactant , as this mass change is converted into nuclear energy and hence Binding energy of product is more than Binding Energy of reactant. Ans hence Product is more stable than reactant.
