IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 8.2 – Thermal energy Transfer
Topic 8 Weightage : 7 %
All Questions for Topic 8.2 – Conduction, convection and thermal radiation , Black-body radiation , Albedo and emissivity , The solar constant , The greenhouse effect , Energy balance in the Earth surface–atmosphere system
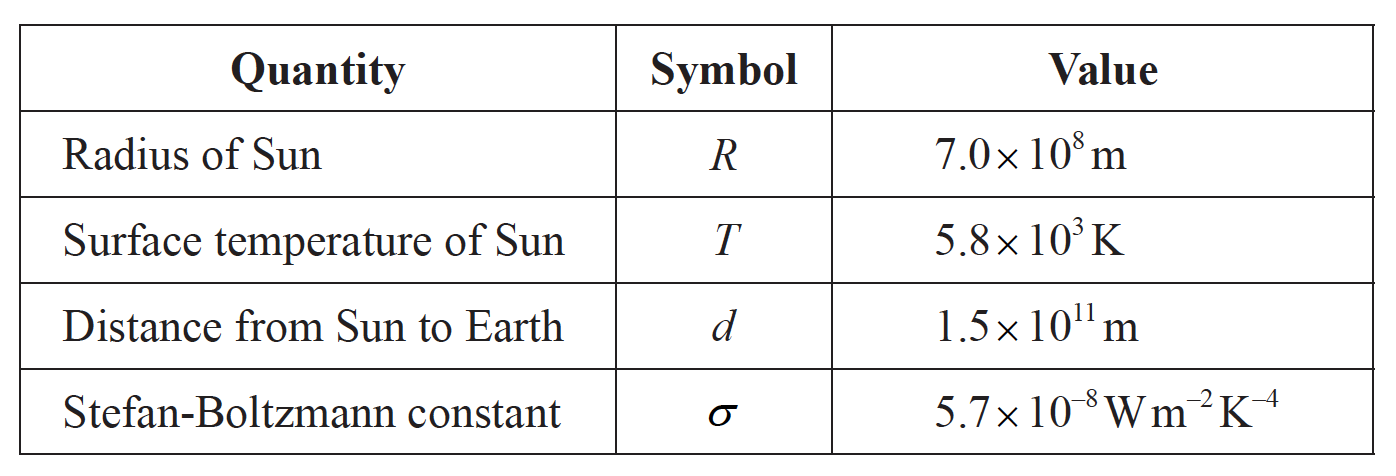
The Sun has a radius of 7.0×108m and is a distance 1.5×1011 m from Earth. The surface temperature of the Sun is 5800 K.
a.Show that the intensity of the solar radiation incident on the upper atmosphere of the Earth is approximately 1400Wm−2.[2]
▶️Answer/Explanation
Markscheme
a.
\(I = \frac{{\sigma A{T^4}}}{{4\pi {d^2}}}\)
\( = \frac{{5.67 \times {{10}^{ – 8}} \times {{\left( {7.0 \times {{10}^8}} \right)}^2} \times {{5800}^4}}}{{{{\left( {1.5 \times {{10}^{11}}} \right)}^2}}}\)
OR \( \frac{{5.67 \times {{10}^{ – 8}} \times 4\pi \times {{\left( {7.0 \times {{10}^8}} \right)}^2} \times {{5800}^4}}}{{4\pi \times {{\left( {1.5 \times {{10}^{11}}} \right)}^2}}}\)
I=1397 Wm−2
In this question we must see 4SF to award MP3.
Allow candidate to add radius of Sun to Earth–Sun distance. Yields 1386 Wm–2.
«transmitted intensity =» 0.70 × 1400 «= 980Wm–2»
\(\frac{{\pi {R^2}}}{{4\pi {R^2}}} \times 980{\rm{W}}{{\rm{m}}^{ – 2}}\)
245Wm–2
5.67 × 10–8 × T4 = 245
T = 256K
This question is in two parts. Part 1 is about solar radiation and the greenhouse effect. Part 2 is about a mass on a spring.
Part 1 Solar radiation and the greenhouse effect
The following data are available.
Part 2 A mass on a spring
An object is placed on a frictionless surface and attached to a light horizontal spring.
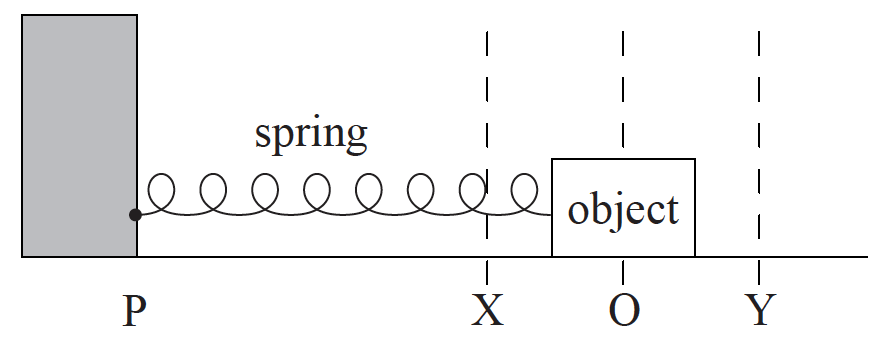
The other end of the spring is attached to a stationary point P. Air resistance is negligible. The equilibrium position is at O. The object is moved to position Y and released.
a.
State the Stefan-Boltzmann law for a black body.[2]
Deduce that the solar power incident per unit area at distance d from the Sun is given by
\[\frac{{\sigma {R^2}{T^4}}}{{{d^2}}}\][2]
Calculate, using the data given, the solar power incident per unit area at distance d from the Sun.[2]
State two reasons why the solar power incident per unit area at a point on the surface of the Earth is likely to be different from your answer in (c).[2]
The average power absorbed per unit area at the Earth’s surface is 240Wm–2. By treating the Earth’s surface as a black body, show that the average surface temperature of the Earth is approximately 250K.[2]
Explain why the actual surface temperature of the Earth is greater than the value in (e).[3]
Outline the conditions necessary for the object to execute simple harmonic motion.[2]
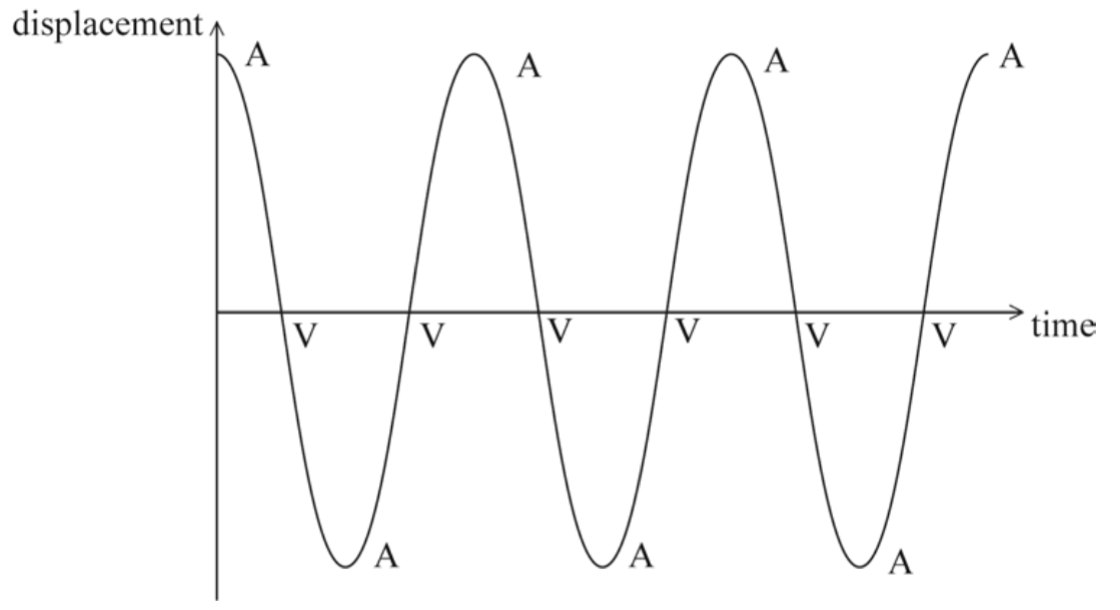
The sketch graph below shows how the displacement of the object from point O varies with time over three time periods.
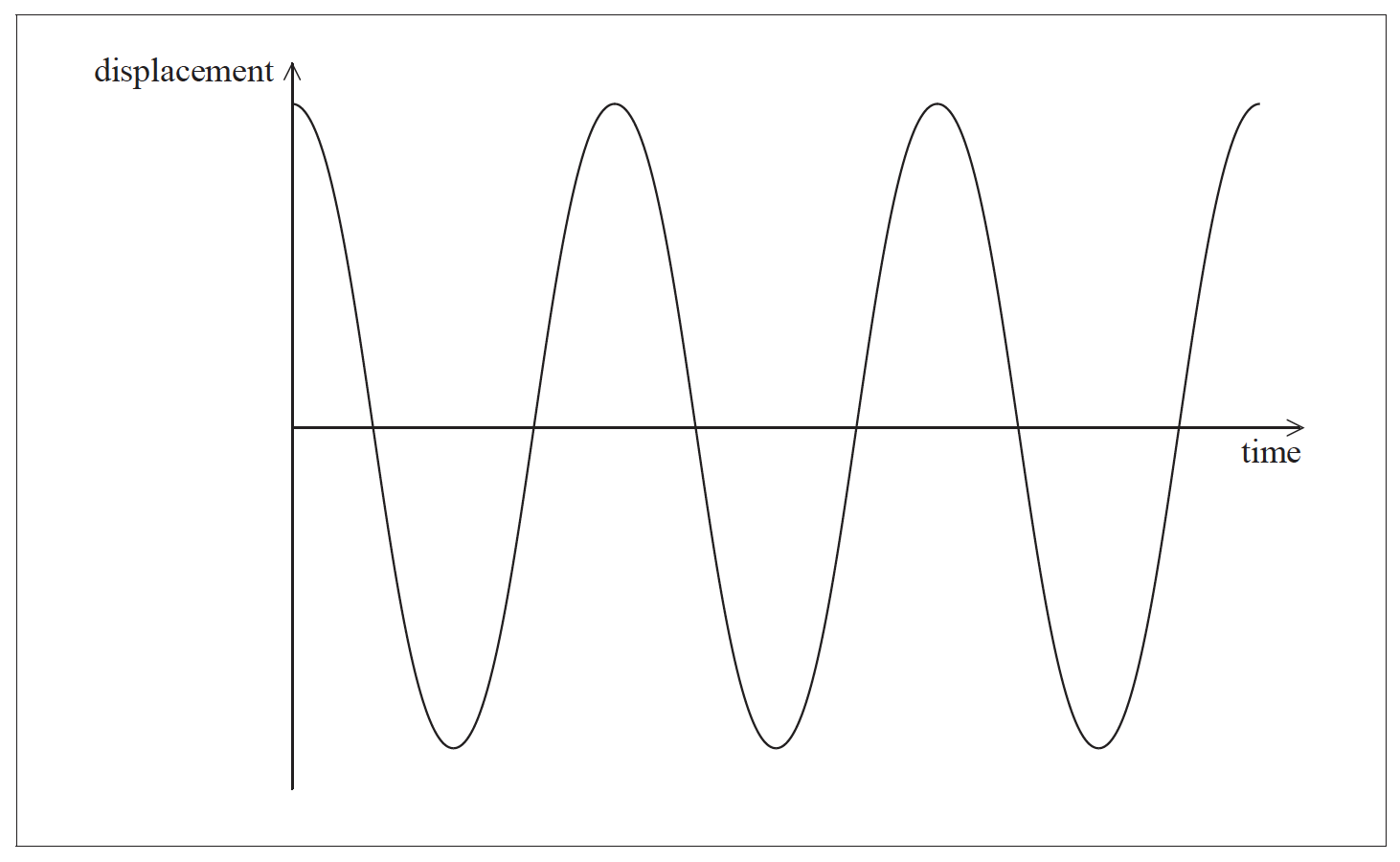
(i) Label with the letter A a point at which the magnitude of the acceleration of the object is a maximum.
(ii) Label with the letter V a point at which the speed of the object is a maximum.
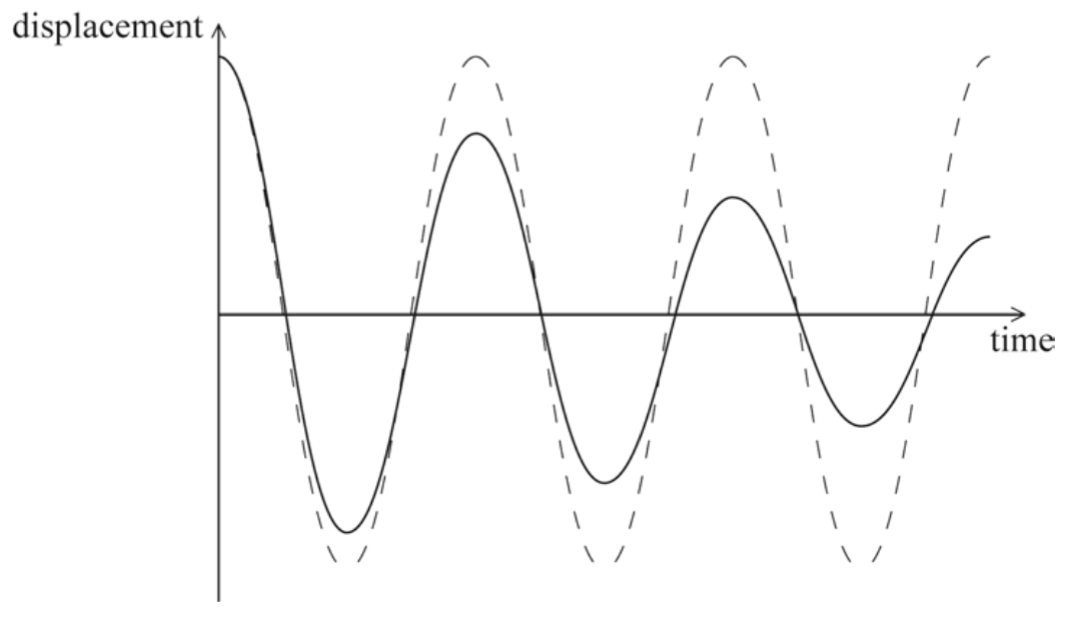
(iii) Sketch on the same axes a graph of how the displacement varies with time if a small frictional force acts on the object.[4]
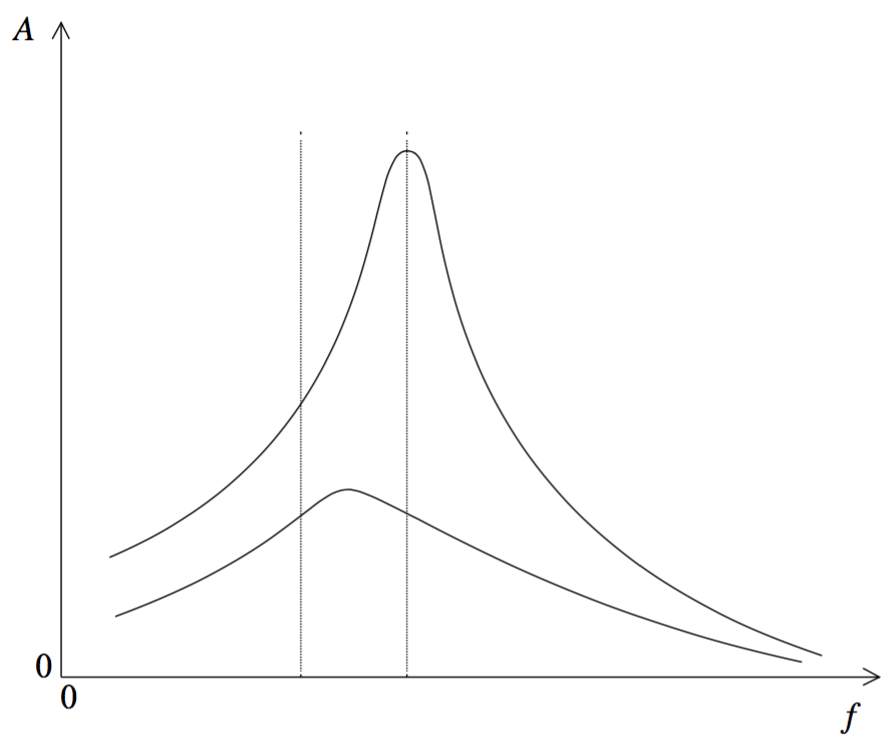
Point P now begins to move from side to side with a small amplitude and at a variable driving frequency f. The frictional force is still small.
At each value of f, the object eventually reaches a constant amplitude A.
The graph shows the variation with f of A.
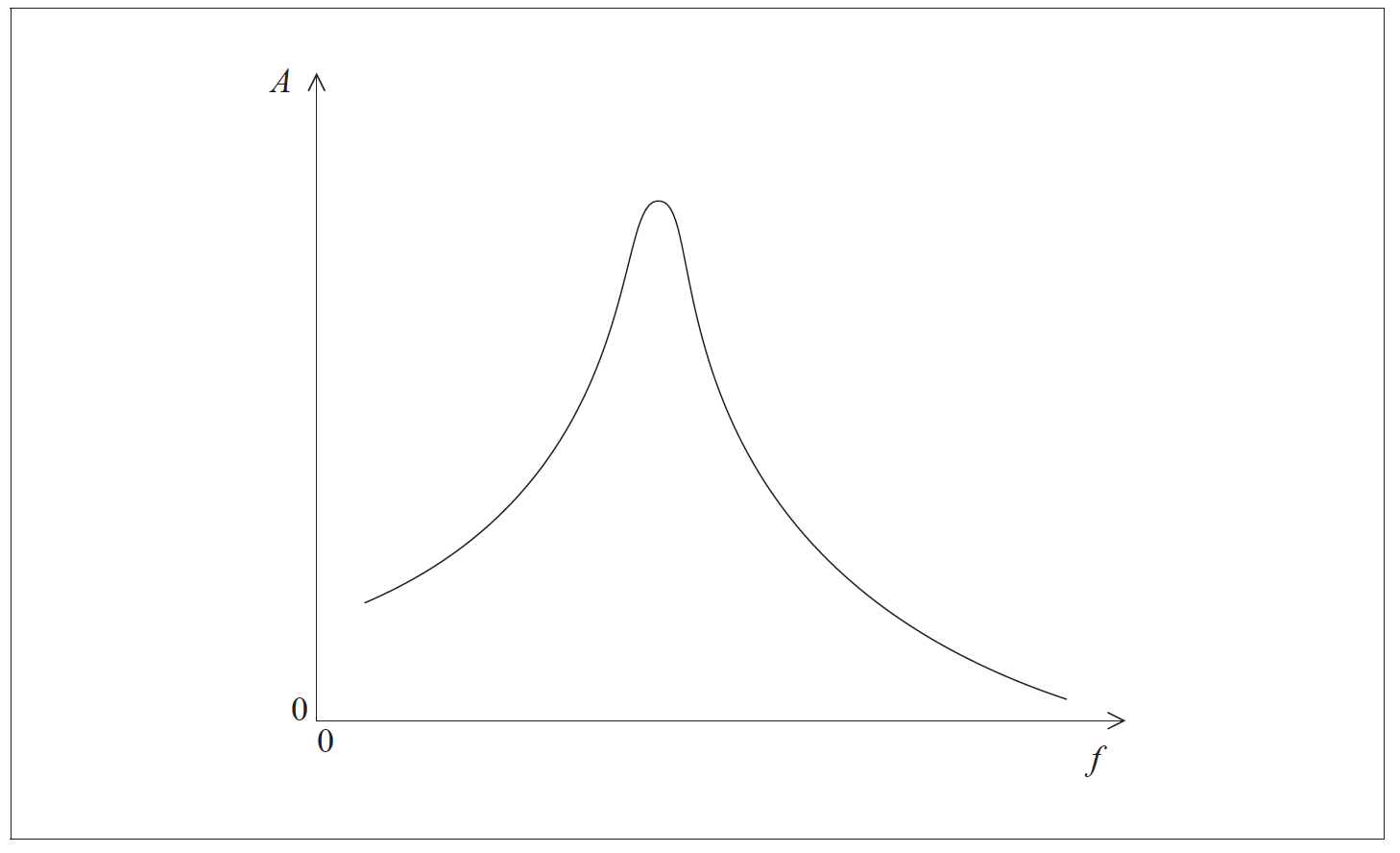
(i) With reference to resonance and resonant frequency, comment on the shape of the graph.
(ii) On the same axes, draw a graph to show the variation with f of A when the frictional force acting on the object is increased.[4]
▶️Answer/Explanation
Markscheme
a.
power/energy per second emitted proportional to surface area;
and proportional to fourth power of absolute temperature / temperature in K;
Accept equation with symbols defined.
solar power given by 4πR2σT 4 ;
spreads out over sphere of surface area 4πd 2 ;
Hence equation given.
\(\left( {\frac{{\sigma {R^2}{T^4}}}{{{d^2}}} = } \right)\frac{{5.7 \times {{10}^{ – 8}} \times {{\left[ {7.0 \times {{10}^8}} \right]}^2} \times {{\left[ {5.8 \times {{10}^3}} \right]}^4}}}{{{{\left[ {1.5 \times {{10}^{11}}} \right]}^2}}}\);
=1.4×103(Wm-2 );
Award [2] for a bald correct answer.
some energy reflected;
some energy absorbed/scattered by atmosphere; depends on latitude;
depends on time of day;
depends on time of year;
depends on weather (eg cloud cover) at location; power output of Sun varies;
Earth-Sun distance varies;
power radiated = power absorbed;
\(T = {}^4\sqrt {\frac{{240}}{{5.7 \times {{10}^{ – 8}}}}} = \left( {250{\rm{K}}} \right)\);
Accept answers given as 260 (K).
radiation from Sun is re-emitted from Earth at longer wavelengths; greenhouse gases in the atmosphere absorb some of this energy; and radiate some of it back to the surface of the Earth;
the force (of the spring on the object)/acceleration (of the object/point O) must be proportional to the displacement (from the equilibrium position/centre/point O);
and in the opposite direction to the displacement / always directed towards the equilibrium position/centre/point O;
(i) one A correctly shown;
(ii) one V correctly shown;
(iii) same period; (judge by eye)
amplitude decreasing with time;
(i) resonance is where driving frequency equals/is close to natural/resonant frequency;
the natural/resonant frequency is at/near the maximum amplitude of the graph;
(ii) lower amplitude everywhere on graph, bit still positive;
maximum in same place/moved slightly (that is, between the lines) to left on graph;