IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 9.1 Simple harmonic motion
Topic 9 Weightage : 5 %
All Questions for Topic 9.1 – The defining equation of SHM , Energy changes
This question is in two parts. Part 1 is about a thermistor circuit. Part 2 is about vibrations and waves.
Part 1 Thermistor circuit
The circuit shows a negative temperature coefficient (NTC) thermistor X and a 100 kΩ fixed resistor R connected across a battery.
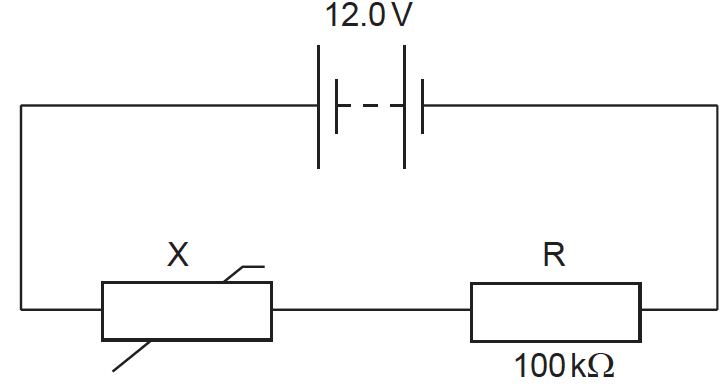
The battery has an electromotive force (emf) of 12.0 V and negligible internal resistance.
Part 2 Vibrations and waves
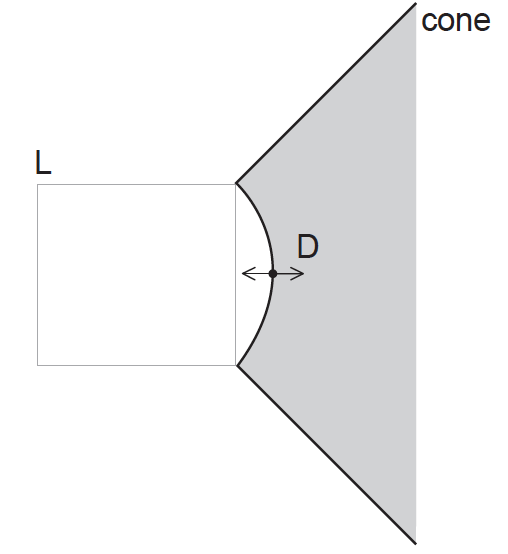
The cone and dust cap D of a loudspeaker L vibrates with a frequency of 1.25 kHz with simple harmonic motion (SHM).
a.(i) Define electromotive force (emf).
(ii) State how the emf of the battery can be measured.[2]
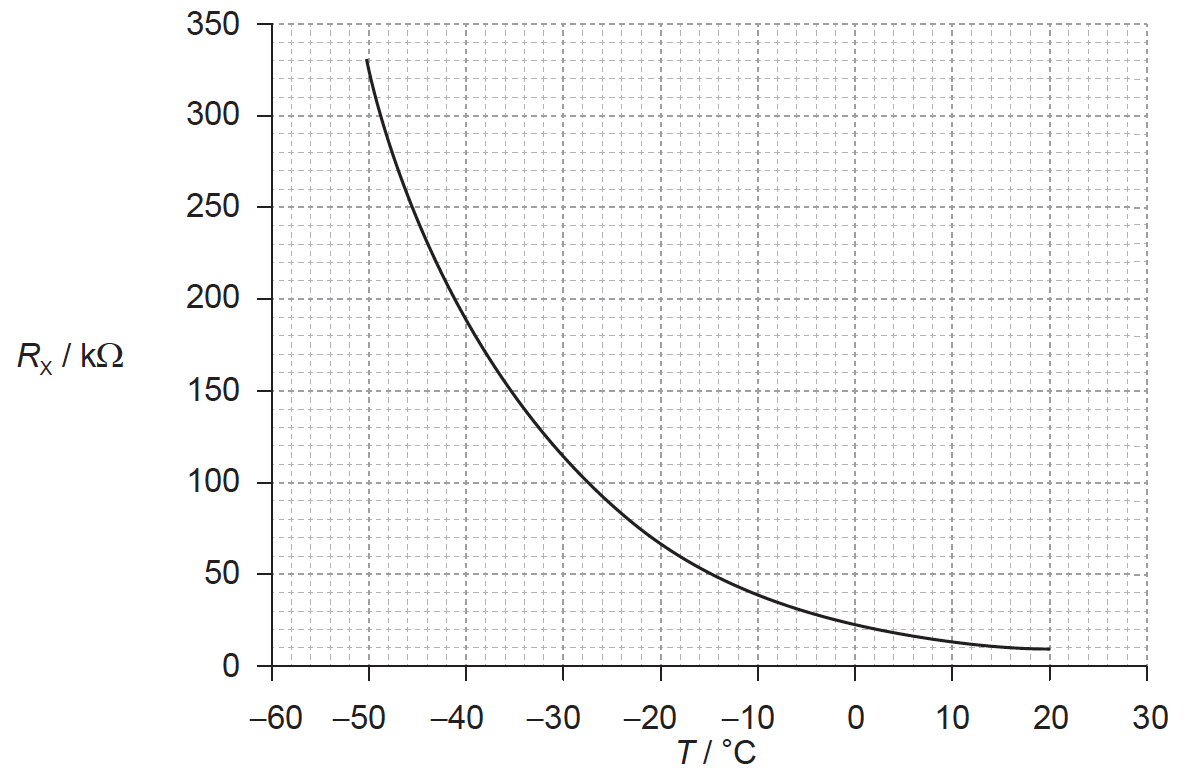
(i) Determine the temperature of X when the potential difference across R is 4.5V.
(ii) State the range of temperatures for which the change in the resistance of the thermistor is most sensitive to changes in temperature.
(iii) State and explain the effect of a decrease in temperature on the ratio
\[\frac{{{\rm{voltage across X}}}}{{{\rm{voltage across R}}}}\].[7]
(i) Calculate the maximum acceleration of D.
(ii) Determine the total energy of D.[4]
(i) Calculate the wavelength of the sound waves.
(ii) Describe the characteristics of sound waves in air.[2]
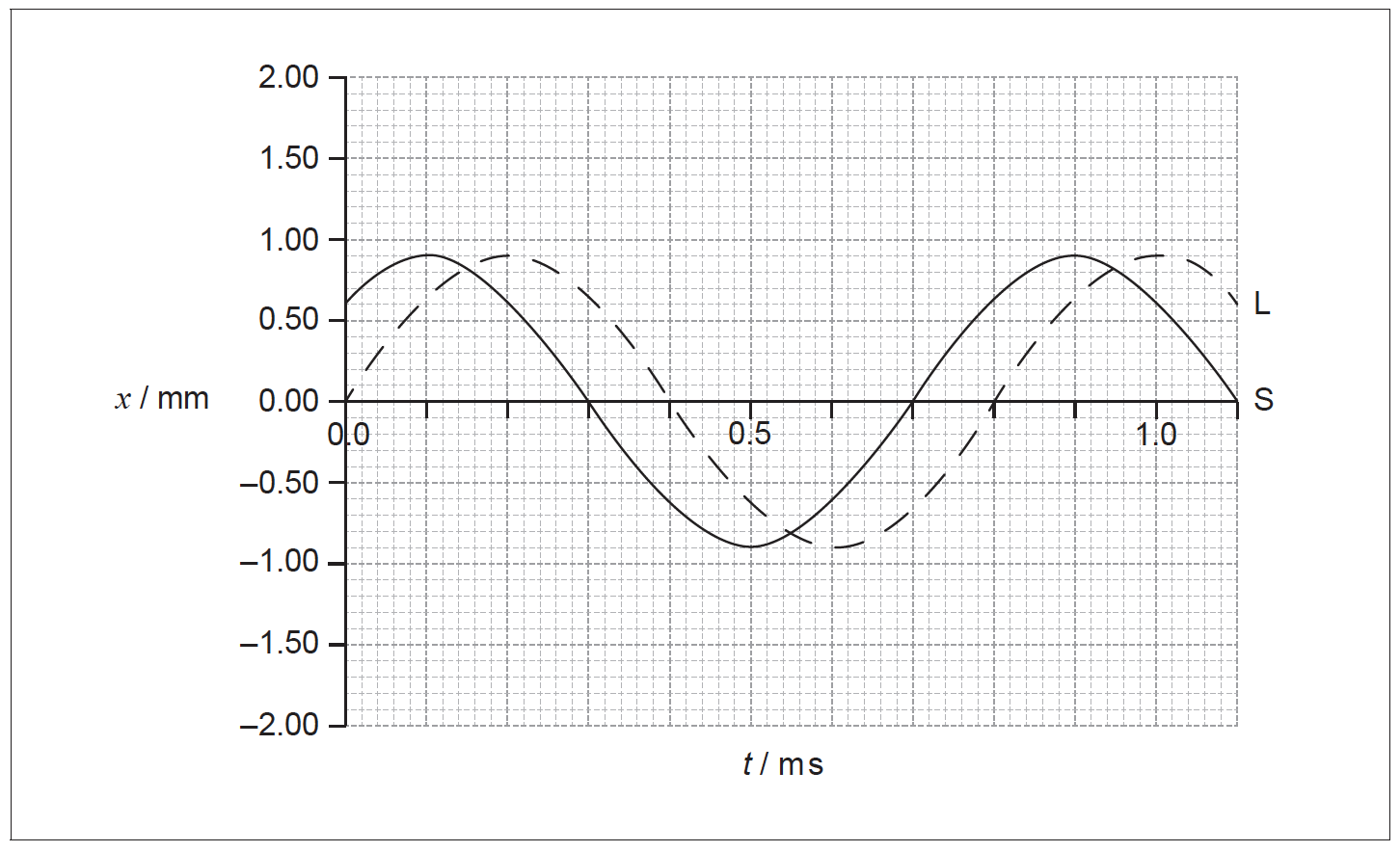
(i) Deduce the relationship between the phase of L and the phase of S.
(ii) On the graph, sketch the variation with t of x for the wave formed by the superposition of the two waves.[6]
▶️Answer/Explanation
Markscheme
a.
(i) the work done per unit charge in moving a quantity of charge completely around a circuit / the power delivered per unit current / work done per unit charge made available by a source;
(ii) place voltmeter across battery;
(i) VX = 7.5 V;
\(I\left( { = \frac{{4.5}}{{100 \times {{10}^3}}}} \right) = 4.5 \times {10^{ – 5}}{\rm{A}}\) or \(\frac{{{V_X}}}{{{V_R}}} = \frac{{{R_x}}}{{{R_R}}}\);
\({R_x}\left( { = \frac{{7.5}}{{4.5 \times {{10}^{ – 5}}}}} \right) = 1.67 \times {10^5}\Omega \) or \({R_x}\left( { = \frac{{7.5}}{{4.5}} \times 100 \times {{10}^3}} \right) = 1.67 \times {10^5}\Omega \);
T= −37 or −38ºC
(ii) −50 to (up to) −30 °C / at low temperatures;
(iii) as the temperature decreases Rx increases;
same current through R and X so the ratio increases or VX increases and VR decreases so the ratio increases;
(periodic) motion in which acceleration/restoring force is proportional to the displacement from a fixed point;
directed towards the fixed point / in the opposite direction to the displacement;
(i) ω=(2πf = 2π×1250)7854 rad s–1;
a0 =(−ω2x0 = −78542 ×0.85×10–3 =) (−)5.2×104 ms−2 ;
(ii) correct substitution into \({E_T} = \frac{1}{2}m{\omega ^2}{x_0}^2\) irrespective of powers of 10;
0.14 to 0.15 J;
(i) 0.264 m;
(ii) longitudinal;
progressive / propagate (through the air) / travels with constant speed (through the air);
series of compressions and rarefactions / high and low (air) pressure;
(i) S leads L / idea that the phase of L is the phase of S minus an angle;
\(\frac{1}{8}\) period / 1×10–4 s / 0.1 ms;
\(\frac{{\rm{\pi }}}{4}\) / 0.79 rad / 45 degrees;
(ii) agreement at all zero displacements;
maxima and minimum at correct times;
constant amplitude of 1.60 mm;
This question is in two parts. Part 1 is about simple harmonic motion (SHM). Part 2 is about current electricity.
Part 1 Simple harmonic motion (SHM)
An object is placed on a frictionless surface. The object is attached by a spring fixed at one end and oscillates at the end of the spring with simple harmonic motion (SHM).
The tension F in the spring is given by F = k x where x is the extension of the spring and k is a constant.
Part 2 Current electricity
a.
Show that \({\omega ^2} = \frac{k}{m}\).[2]
One cycle of the variation of displacement with time is shown for two separate mass–spring systems, A and B.
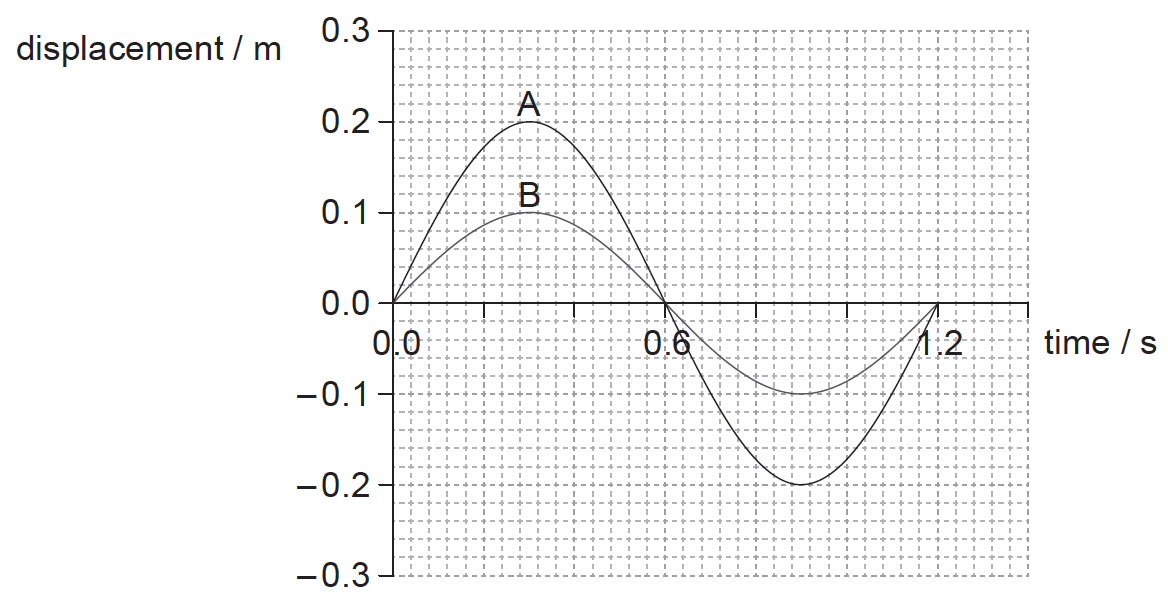
(i) Calculate the frequency of the oscillation of A.
(ii) The springs used in A and B are identical. Show that the mass in A is equal to the mass in B.[3]
The graph shows the variation of the potential energy of A with displacement.
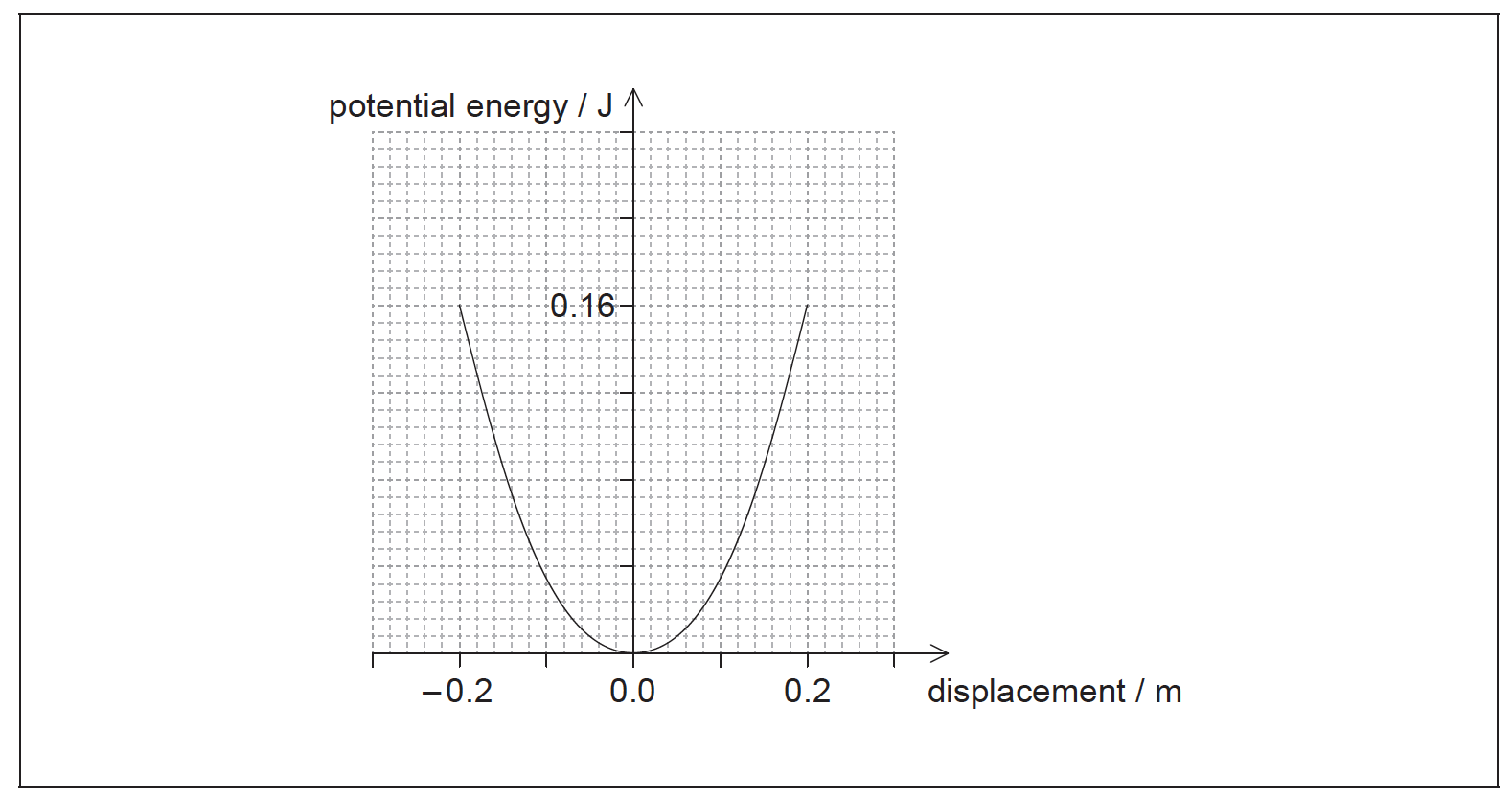
On the axes,
(i) draw a graph to show the variation of kinetic energy with displacement for the mass in A. Label this A.
(ii) sketch a graph to show the variation of kinetic energy with displacement for the mass in B. Label this B.[5]
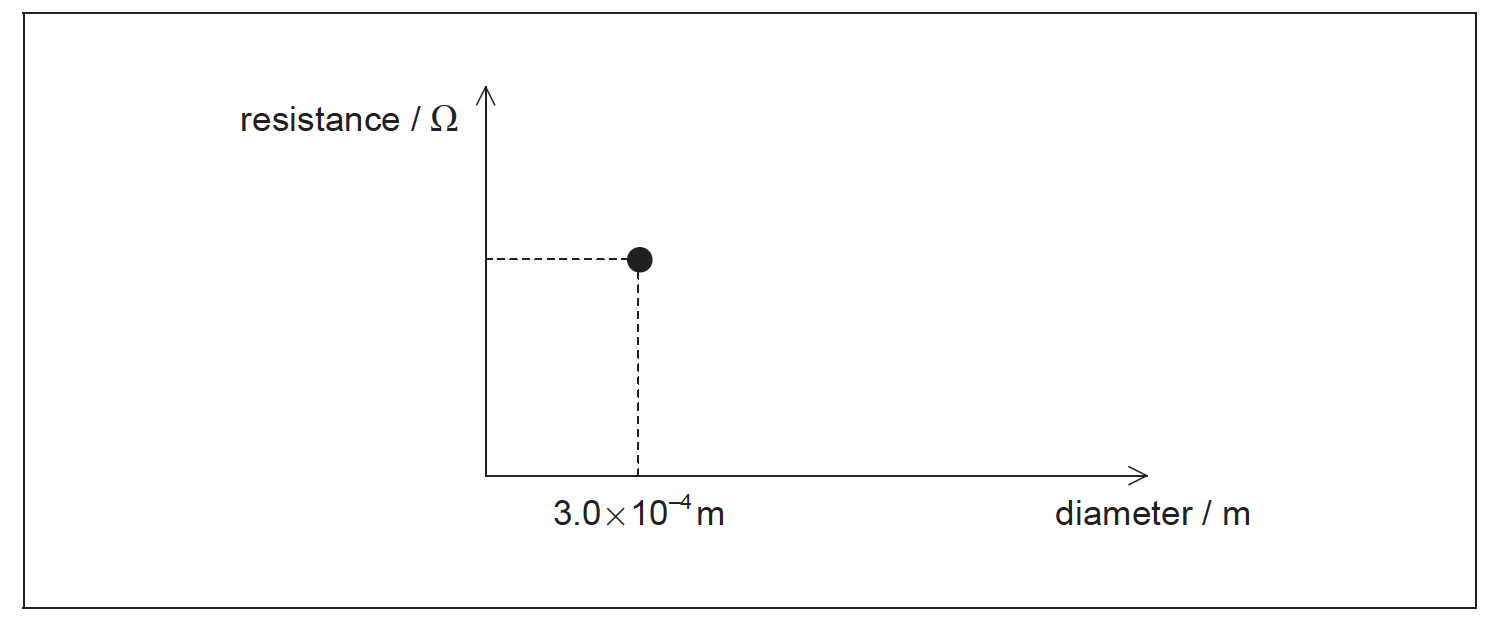
A 24 Ω resistor is made from a conducting wire.
(i) The diameter of the wire is 0.30 mm and the wire has a resistivity of 1.7\( \times \)10–8Ωm. Calculate the length of the wire.
(ii) On the axes, draw a graph to show how the resistance of the wire in (d)(i) varies with the diameter of the wire when the length is constant. The data point for the diameter of 0.30 mm has already been plotted for you.
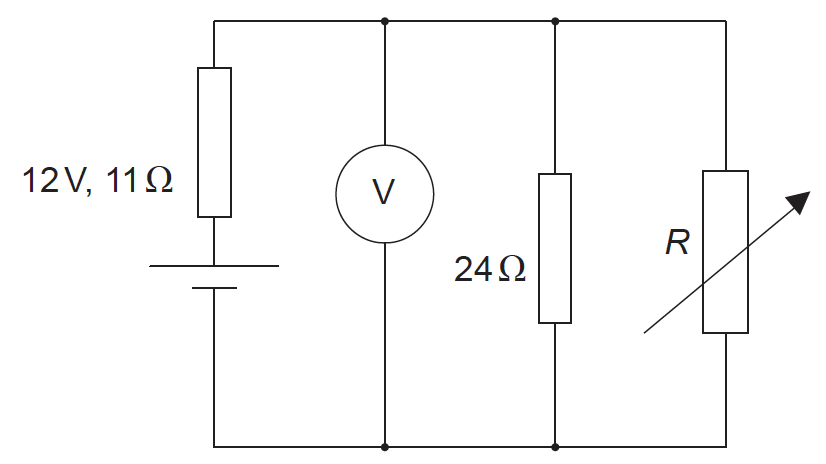
Power supplies deliver maximum power to an external circuit when the resistance of the external circuit equals the internal resistance of the power supply.
(i) Determine the value of R for this circuit at which maximum power is delivered to the external circuit.
(ii) Calculate the reading on the voltmeter for the value of R you determined in (f)(i).
(iii) Calculate the total power dissipated in the circuit when the maximum power is being delivered to the external circuit.[8]
▶️Answer/Explanation
Markscheme
a.
ma \(= – \)kx;
\(a = – \frac{k}{m}x\); (condone lack of negative sign)
\(\left( {{\omega ^2} = \frac{k}{m}} \right)\)
or
implied use of defining equation for simple harmonic motion \(a = – {\omega ^2}x\);
\(\left( {{\rm{so }}{\omega ^2} = \frac{k}{m}} \right)\)
\(ma = – kx\) so \(a = – \left( {\frac{k}{m}} \right)x\);
(i) 0.833 (Hz);
(ii) frequency/period is the same so ω is the same;
k is the same (as springs are identical);
(so m is the same)
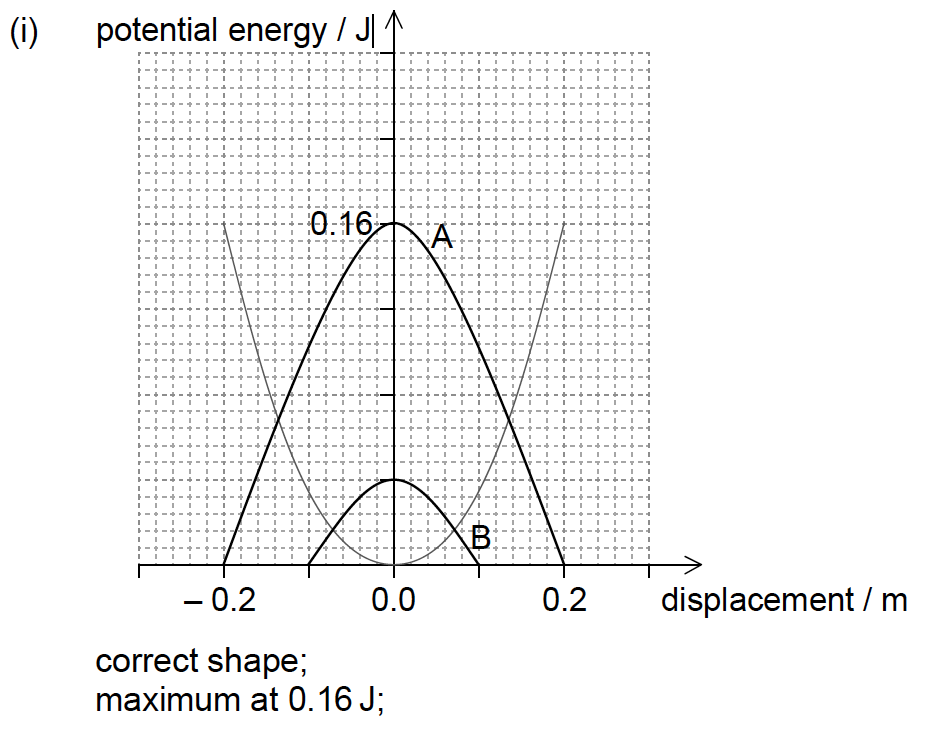
(ii) end displacements correct \( \pm \) 0.01m;
maximum lower than 0.16J;
maximum equal to 0.04J \( \pm \) half square;
(i) \(l = \frac{{\pi {d^2}R}}{{4\rho }}\) seen / correct substitution
into equation: \(24 = \frac{{l \times 1.7 \times {{10}^{ – 8}}}}{{\pi \times {{\left( {0.15 \times {{10}^{ – 3}}} \right)}^2}}}\); } (condone use of r for \(\frac{d}{2}\) in first alternative)
99.7 (m);
Award [2] for bald correct answer.
Award [1 max] if area is incorrectly calculated, answer is 399 m if conversion to radius ignored, ie: allow ECF for second marking point if area is incorrect provided working clear.
(ii) any line showing resistance decreasing with increasing diameter and touching
point;
correct curved shape showing asymptotic behavior on at least one axis;
current/conduction is (related to) flow of charge;
conductors have many electrons free/unbound / electrons are the charge carriers / insulators have few free electrons;
pd/electric field accelerates/exerts force on electrons;
smaller current in insulators as fewer electrons available / larger current in conductors as more electrons available;
(i) use of total resistance = 11Ω; (can be seen in second marking point)
\(\frac{1}{{11}} = \frac{1}{R} + \frac{1}{{24}}\);
20.3(Ω) ;
(ii) as current is same in resistor network and cell and resistance is same, half of emf must appear across resistor network;
6.0 (V);
or
\(I = \frac{{12}}{{\left( {11 + 11} \right)}} = 0.545\left( {\rm{A}} \right)\);
V=(0.545×11=) 6.0 (V);
Other calculations are acceptable.
Award [2] for a bald correct answer.
(iii) use of 22 (ohm) or 11+11 (ohm) seen;
use of \(\frac{{{V^2}}}{R}\) or equivalent;
6.54 (W);
Award [3] for bald correct answer.
Award [2 max] if cell internal resistance ignored, yields 3.27 V.