IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.2 Single slit diffraction
Topic 9 Weightage : 5 %
All Questions for Topic 9.2 – The nature of single-slit diffraction
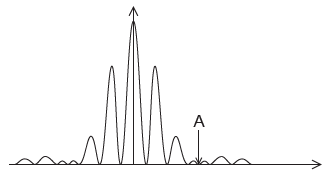
Yellow light from a sodium lamp of wavelength 590 nm is incident at normal incidence on a double slit. The resulting interference pattern is observed on a screen. The intensity of the pattern on the screen is shown.
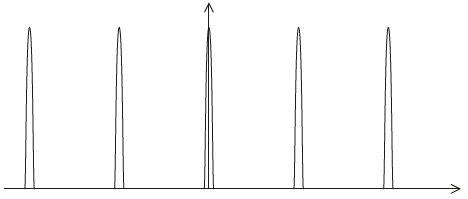
The double slit is replaced by a diffraction grating that has 600 lines per millimetre. The resulting pattern on the screen is shown.
a.i.
Explain why zero intensity is observed at position A.[2]
The distance from the centre of the pattern to A is 4.1 x 10–2 m. The distance from the screen to the slits is 7.0 m.
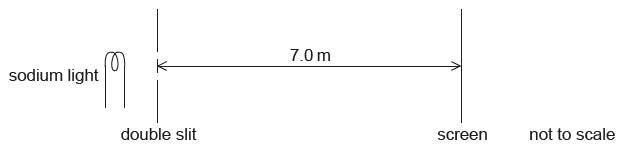
Calculate the width of each slit.[2]
Calculate the separation of the two slits.[2]
State and explain the differences between the pattern on the screen due to the grating and the pattern due to the double slit.[3]
The yellow light is made from two very similar wavelengths that produce two lines in the spectrum of sodium. The wavelengths are 588.995 nm and 589.592 nm. These two lines can just be resolved in the second-order spectrum of this diffraction grating. Determine the beam width of the light incident on the diffraction grating.[3]
▶️Answer/Explanation
Markscheme
a.i.
the diagram shows the combined effect of «single slit» diffraction and «double slit» interference
recognition that there is a minimum of the single slit pattern
OR
a missing maximum of the double slit pattern at A
waves «from the single slit» are in antiphase/cancel/have a path difference of (n + \(\frac{1}{2}\))λ/destructive interference at A
θ = \(\frac{{4.1 \times {{10}^{ – 2}}}}{{7.0}}\) OR b = \(\frac{\lambda }{\theta }\) «= \(\frac{{7.0 \times 5.9 \times {{10}^{ – 7}}}}{{4.1 \times {{10}^{ – 2}}}}\)»
1.0 × 10–4 «m»
Award [0] for use of double slit formula (which gives the correct answer so do not award BCA)
Allow use of sin or tan for small angles
use of s = \(\frac{{\lambda D}}{d}\) with 3 fringes «\(\frac{{590 \times {{10}^{ – 9}} \times 7.0}}{{4.1 \times {{10}^{ – 2}}}}\)»
3.0 x 10–4 «m»
Allow ECF.
fringes are further apart because the separation of slits is «much» less
intensity does not change «significantly» across the pattern or diffraction envelope is broader because slits are «much» narrower
the fringes are narrower/sharper because the region/area of constructive interference is smaller/there are more slits
intensity of peaks has increased because more light can pass through
Award [1 max] for stating one or more differences with no explanation
Award [2 max] for stating one difference with its explanation
Award [MP3] for a second difference with its explanation
Allow “peaks” for “fringes”
Δλ = 589.592 – 588.995
OR
Δλ = 0.597 «nm»
N = «\(\frac{\lambda }{{m\Delta \lambda }}\) =» \(\frac{{589}}{{2 \times 0.597}}\) «493»
beam width = «\(\frac{{493}}{{600}}\) =» 8.2 x 10–4 «m» or 0.82 «mm»
Monochromatic light is incident normally on four thin, parallel, rectangular slits.
The graph shows the variation with diffraction angle θ of the intensity of light I at a distant screen.
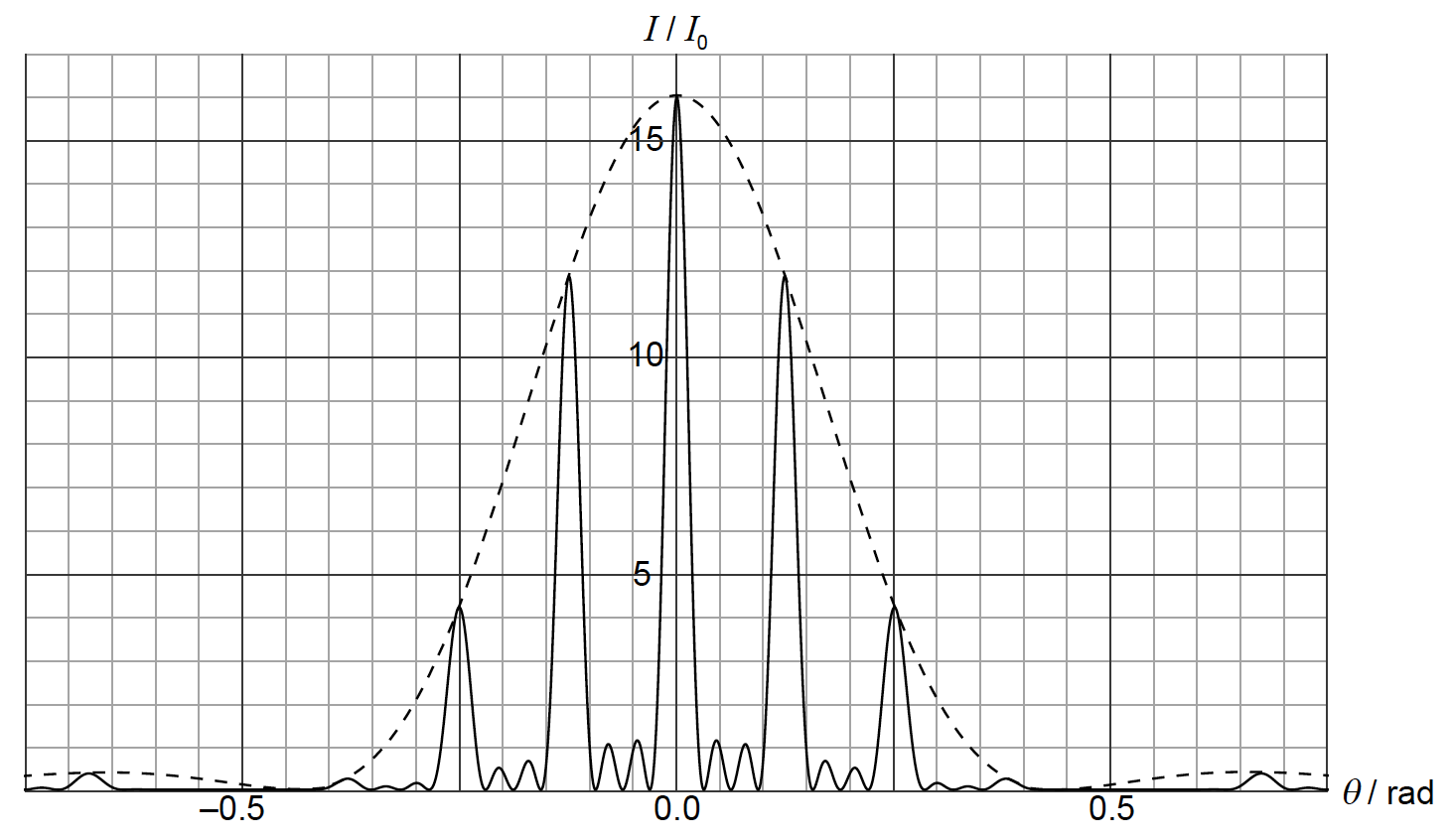
I0 is the intensity of the light at the middle of the screen from one slit.
a.
Explain why the intensity of light at θ=0 is 16I0.[3]
The width of each slit is 1.0μm. Use the graph to
(i) estimate the wavelength of light.
(ii) determine the separation of two consecutive slits.[4]
(i) State two changes to the graph on page 20 as a result of these modifications.
(ii) A diffraction grating is used to resolve two lines in the spectrum of sodium in the second order. The two lines have wavelengths 588.995nm and 589.592nm.
Determine the minimum number of slits in the grating that will enable the two lines to be resolved.[4]
▶️Answer/Explanation
Markscheme
a.
constructive interference
amplitude/amount of light from 4 slits is 4 × amplitude «from one slit»
intensity is proportional to amplitude2 OR shows 42 = 16 in context of intensity
(i)
«diffraction minimum at» θ=0.43rad
\(\lambda = \ll b\theta = 1.0 \times {10^{ – 6}} \times 0.43 = \gg 4.3 \times {10^{ – 7}}{\rm{m}}\)
Accept θ in range 0.41 to 0.45 rad.
Allow λ=bsinθ but do not allow nλ=dsinθ.
Award [1 max] for solution using factor of 1.22.
Award [0] if use of \(s = \frac{{\lambda D}}{d}\) seen.
(ii)
«first secondary maximum at» θ=0.125rad
\(d = \frac{{1 \times {\rm{value from (b)(i)}}}}{{\sin 0.125}} = 3.4 \times {10^{ – 6}}{\rm{m}}\)
Accept q in range 0.123 to 0.127 rad.
Sine must be seen to award MP2.
Allow ECF from (b)(i).
Allow use of 2nd or 3rd maxima (0.25 rad and 3.46 μm or 0.375 rad and 3.5 μm with appropriate n).
(i)
primary maxima/fringes become brighter/more intense
primary maxima become narrower/sharper
secondary maxima become unimportant/less intense/disappear
Insist on “secondary” for MP3.
(ii)
\(N = \ll \frac{{\bar \lambda }}{{m\Delta \lambda }} = \gg \frac{{589.2935}}{{2 \times 0.5970}}\)
N=494 or 500
Allow use of 588.995 nm or 589.592 nm for \({\bar \lambda }\).
This question is about the properties of waves.
Microwaves from a microwave transmitter are reflected from two parallel sheets, A and B. Sheet A partially reflects microwave energy while allowing some to pass through. All of the microwave energy incident on sheet B is reflected.
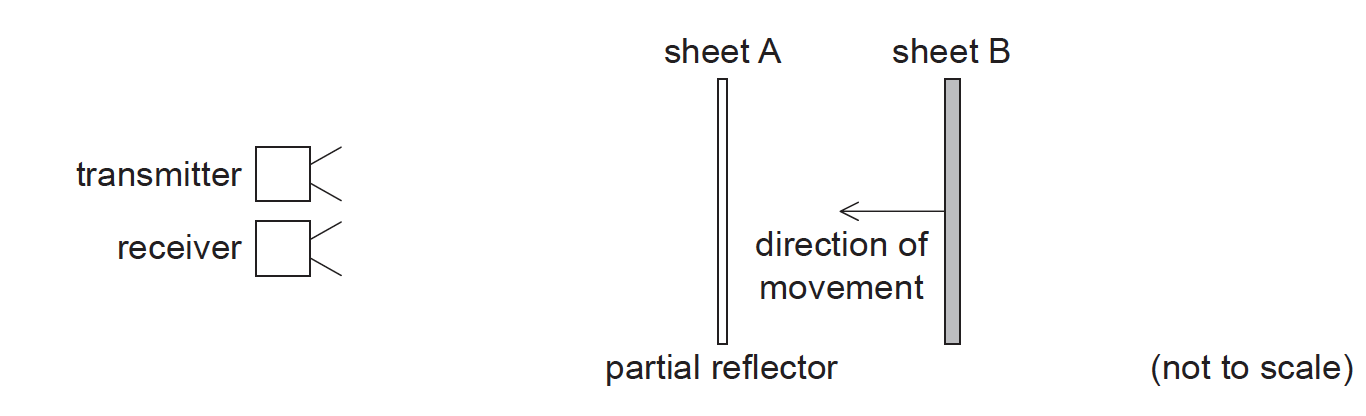
Sheet A is fixed and sheet B is moved towards it. While sheet B is moving, the intensity of the signal detected at the receiver goes through a series of maximum and minimum values.
a.
Outline why a minimum in the intensity occurs for certain positions of sheet B.[3]
The apparatus is arranged to demonstrate diffraction effects.
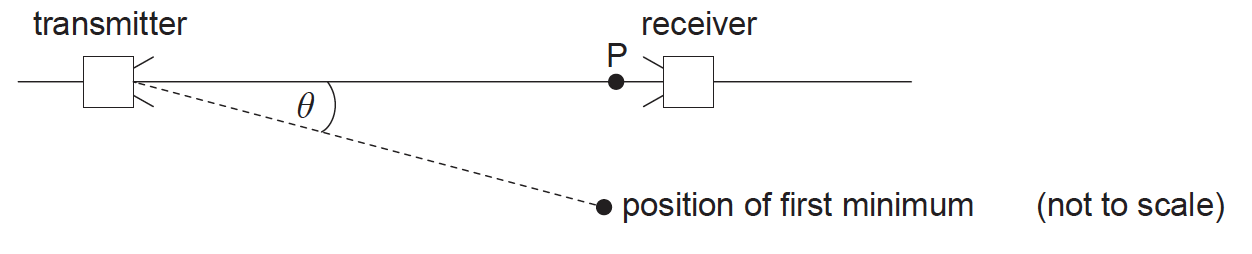
The microwaves emerge from the transmitter through an aperture that acts as a single slit.
(i) Outline what is meant by diffraction.
(ii) A maximum signal strength is observed at P. When the receiver is moved through an angle \(\theta \), a first minimum is observed. The width of the aperture of the transmitter is 60 mm. Estimate the value of \(\theta \).[3]
Microwaves can be used to demonstrate polarization effects. Outline why an ultrasound receiver and transmitter cannot be used to demonstrate polarization.[2]
▶️Answer/Explanation
Markscheme
a.
mention of interference;
interference is between reflected waves from both reflectors;
minimum caused (by destructive interference) when crest meets trough/when path difference is \(\frac{\lambda }{2}\) / (completely) out of phase / phase difference of \(\pi \)/180º / OWTTE;
minimum occurs when twice the distance between plates is \(\left( {n + \frac{1}{2}} \right)\lambda \);
Ignore references to standing waves.
(i) spreading out of a wave; (do not allow “bending” even if context is obstacle)
when it meets an aperture/gap/slit/obstacle;
Allow credit for answers appearing on clear labelled diagram for both marks.
(ii) \(\left( {\theta = \frac{{32}}{{60}} = } \right)0.533\left( {{\rm{rad}}} \right)\) or 30.6(º);
Award [0] for calculation that uses 1.22 (0.65 rad).
Award [0] for 0.533º or 30.6 rad.
At least one centre is using the abbreviation c for rad. Please allow this.
sound waves (in air) are longitudinal;
longitudinal waves cannot be polarized / only transverse waves can be polarized;
Award [0] for any suggestion that ultrasound is an electromagnetic wave.
