IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.3 Interference
Topic 9 Weightage : 5 %
All Questions for Topic 9.3 – Young’s double-slit experiment , Modulation of two-slit interference pattern by one-slit diffraction effect , Multiple slit and diffraction grating interference patterns , Thin film interference
a.
Monochromatic light from two identical lamps arrives on a screen.
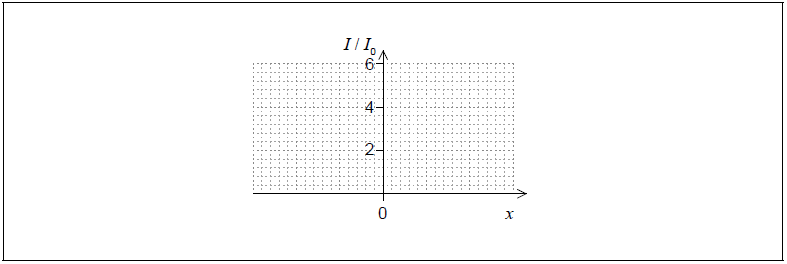
The intensity of light on the screen from each lamp separately is I0.
On the axes, sketch a graph to show the variation with distance x on the screen of the intensity I of light on the screen.
 [1]
[1]
Monochromatic light from a single source is incident on two thin, parallel slits.
The following data are available.
\[\begin{array}{*{20}{l}} {{\text{Slit separation}}}&{ = 0.12{\text{ mm}}} \\ {{\text{Wavelength}}}&{ = 680{\text{ nm}}} \\ {{\text{Distance to screen}}}&{ = 3.5{\text{ m}}} \end{array}\]
The intensity I of light at the screen from each slit separately is I0. Sketch, on the axes, a graph to show the variation with distance x on the screen of the intensity of light on the screen for this arrangement.
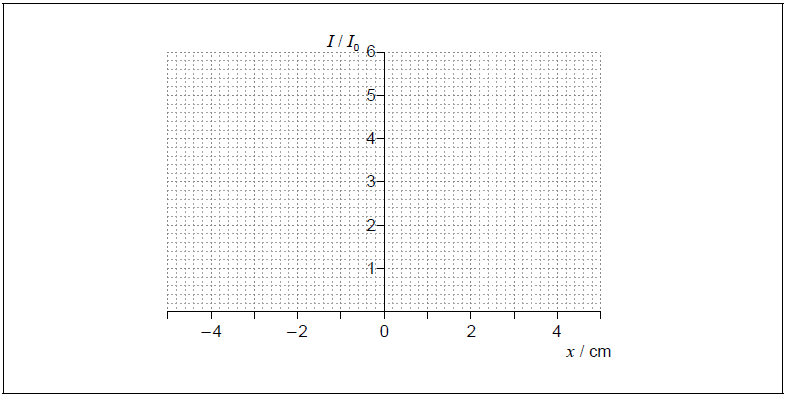 [3]
[3]
The slit separation is increased. Outline one change observed on the screen.[1]
▶️Answer/Explanation
Markscheme
a.
horizontal straight line through I = 2
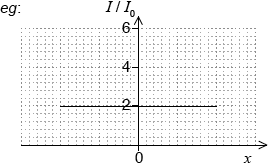
Accept a curve that falls from I = 2 as distance increases from centre but not if it falls to zero.
[1 mark]
«standard two slit pattern»
general shape with a maximum at x = 0
maxima at 4I0
maxima separated by «\(\frac{{D\lambda }}{s}\) =» 2.0 cm
Accept single slit modulated pattern provided central maximum is at 4. ie height of peaks decrease as they go away from central maximum. Peaks must be of the same width
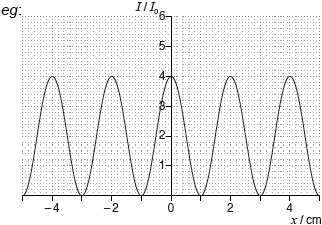
[3 marks]
fringe width/separation decreases
OR
more maxima seen[1 mark]
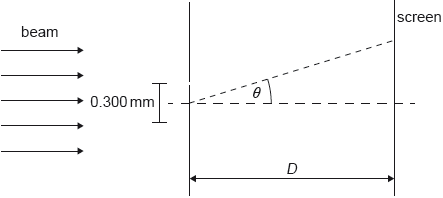
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
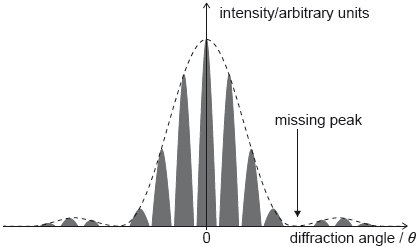
The graph of variation of intensity with diffraction angle for this experiment is shown.
a.ii.
Outline why the beam has to be coherent in order for the fringes to be visible.[1]
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.[3]
Deduce, in mm, the width of one slit.[2]
The wavelength of the light in the beam when emitted by the galaxy was 621.4 nm.
Explain, without further calculation, what can be deduced about the relative motion of the galaxy and the Earth.[2]
▶️Answer/Explanation
Markscheme
a.ii.
light waves (from slits) must have constant phase difference / no phase difference / be in phase
OWTTE
[1 mark]
sin θ = \(\frac{{4 \times 633.0 \times {{10}^{ – 9}}}}{{0.300 \times {{10}^{ – 3}}}}\)
sin θ = 0.0084401…
final answer to three sig figs (eg 0.00844 or 8.44 × 10–3)
Allow ECF from (a)(iii).
Award [1] for 0.121 rad (can award MP3 in addition for proper sig fig)
Accept calculation in degrees leading to 0.481 degrees.
Award MP3 for any answer expressed to 3sf.
[3 marks]
use of diffraction formula «b = \(\frac{\lambda }{\theta }\)»
OR
\(\frac{{633.0 \times {{10}^{ – 9}}}}{{0.00844}}\)
«=» 7.5«00» × 10–2 «mm»
Allow ECF from (b)(i).
[2 marks]
wavelength increases (so frequency decreases) / light is redshifted
galaxy is moving away from Earth
Allow ECF for MP2 (ie wavelength decreases so moving towards).
[2 marks]
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.

The graph of variation of intensity with diffraction angle for this experiment is shown.

a.ii.
Outline why the beam has to be coherent in order for the fringes to be visible.[1]
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.[3]
Deduce, in mm, the width of one slit.[2]
The wavelength of the light in the beam when emitted by the galaxy was 621.4 nm.
Explain, without further calculation, what can be deduced about the relative motion of the galaxy and the Earth.[2]
▶️Answer/Explanation
Markscheme
a.ii.
light waves (from slits) must have constant phase difference / no phase difference / be in phase
OWTTE
[1 mark]
sin θ = \(\frac{{4 \times 633.0 \times {{10}^{ – 9}}}}{{0.300 \times {{10}^{ – 3}}}}\)
sin θ = 0.0084401…
final answer to three sig figs (eg 0.00844 or 8.44 × 10–3)
Allow ECF from (a)(iii).
Award [1] for 0.121 rad (can award MP3 in addition for proper sig fig)
Accept calculation in degrees leading to 0.481 degrees.
Award MP3 for any answer expressed to 3sf.
[3 marks]
use of diffraction formula «b = \(\frac{\lambda }{\theta }\)»
OR
\(\frac{{633.0 \times {{10}^{ – 9}}}}{{0.00844}}\)
«=» 7.5«00» × 10–2 «mm»
Allow ECF from (b)(i).
[2 marks]
wavelength increases (so frequency decreases) / light is redshifted
galaxy is moving away from Earth
Allow ECF for MP2 (ie wavelength decreases so moving towards).
[2 marks]
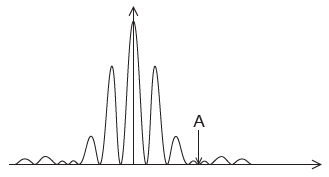
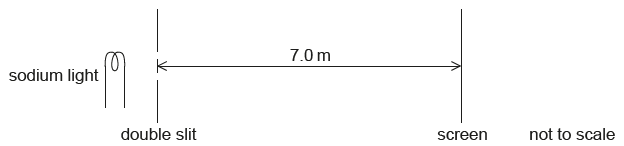
Yellow light from a sodium lamp of wavelength 590 nm is incident at normal incidence on a double slit. The resulting interference pattern is observed on a screen. The intensity of the pattern on the screen is shown.
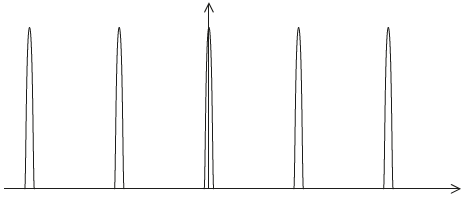
The double slit is replaced by a diffraction grating that has 600 lines per millimetre. The resulting pattern on the screen is shown.
a.i.
Explain why zero intensity is observed at position A.[2]
The distance from the centre of the pattern to A is 4.1 x 10–2 m. The distance from the screen to the slits is 7.0 m.
Calculate the width of each slit.[2]
Calculate the separation of the two slits.[2]
State and explain the differences between the pattern on the screen due to the grating and the pattern due to the double slit.[3]
The yellow light is made from two very similar wavelengths that produce two lines in the spectrum of sodium. The wavelengths are 588.995 nm and 589.592 nm. These two lines can just be resolved in the second-order spectrum of this diffraction grating. Determine the beam width of the light incident on the diffraction grating.[3]
▶️Answer/Explanation
Markscheme
a.i.
the diagram shows the combined effect of «single slit» diffraction and «double slit» interference
recognition that there is a minimum of the single slit pattern
OR
a missing maximum of the double slit pattern at A
waves «from the single slit» are in antiphase/cancel/have a path difference of (n + \(\frac{1}{2}\))λ/destructive interference at A
θ = \(\frac{{4.1 \times {{10}^{ – 2}}}}{{7.0}}\) OR b = \(\frac{\lambda }{\theta }\) «= \(\frac{{7.0 \times 5.9 \times {{10}^{ – 7}}}}{{4.1 \times {{10}^{ – 2}}}}\)»
1.0 × 10–4 «m»
Award [0] for use of double slit formula (which gives the correct answer so do not award BCA)
Allow use of sin or tan for small angles
use of s = \(\frac{{\lambda D}}{d}\) with 3 fringes «\(\frac{{590 \times {{10}^{ – 9}} \times 7.0}}{{4.1 \times {{10}^{ – 2}}}}\)»
3.0 x 10–4 «m»
Allow ECF.
fringes are further apart because the separation of slits is «much» less
intensity does not change «significantly» across the pattern or diffraction envelope is broader because slits are «much» narrower
the fringes are narrower/sharper because the region/area of constructive interference is smaller/there are more slits
intensity of peaks has increased because more light can pass through
Award [1 max] for stating one or more differences with no explanation
Award [2 max] for stating one difference with its explanation
Award [MP3] for a second difference with its explanation
Allow “peaks” for “fringes”
Δλ = 589.592 – 588.995
OR
Δλ = 0.597 «nm»
N = «\(\frac{\lambda }{{m\Delta \lambda }}\) =» \(\frac{{589}}{{2 \times 0.597}}\) «493»
beam width = «\(\frac{{493}}{{600}}\) =» 8.2 x 10–4 «m» or 0.82 «mm»
