This question is about diffraction and resolution.
Two identical sources of electromagnetic radiation, S1 and S2, emit monochromatic coherent waves of wavelength 59 μm. The waves pass through a circular aperture and are incident on a screen.
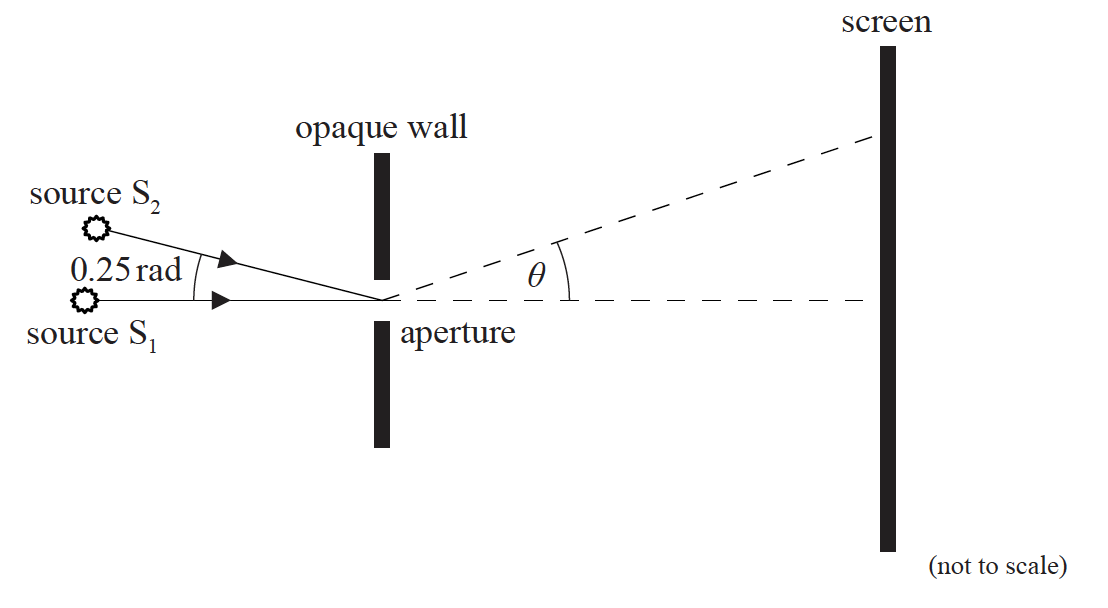
S1 and S2 are at the same distance from the aperture. The diameter of the aperture is 0.18 mm. The angle between the lines joining the sources to the aperture is 0.25 rad.
S1 is turned on and S2 is turned off.
(i) Show that the angle at which the first minimum of the diffraction pattern occurs is 0.40 rad.
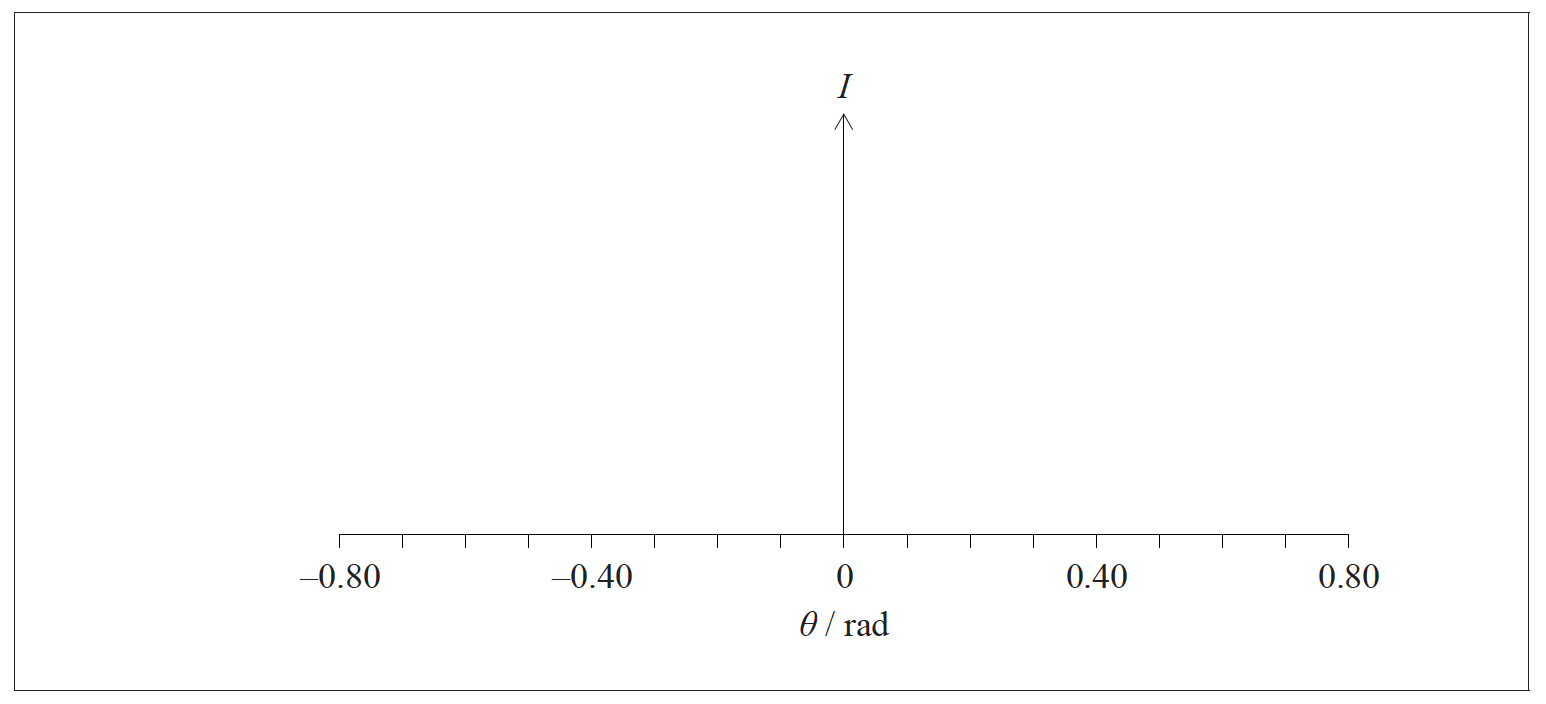
(ii) On the axes below, sketch a graph to show how the intensity I of the radiation from S1 varies with the diffraction angle θ.
▶️Answer/Explanation
Markscheme
(i) \(\theta = \frac{{1.22 \times 59 \times {{10}^{ – 6}}}}{{0.18 \times {{10}^{ – 3}}}}\);
(=0.40rad)
(ii) central symmetrical maximum;
at least one secondary maximum on each side, no more than one third the height of the central maximum; (judge by eye)
minima drawn to zero, ie touching axis at θ=±0.40 (and ±0.80);
This question is about standing waves and the Doppler effect.
The horn of a train can be modeled as a pipe with one open end and one closed end. The speed of sound in air is 330ms–1.

a.On leaving the station, the train blows its horn. Both the first harmonic and the next highest harmonic are produced by the horn. The difference in frequency between the harmonics emitted by the horn is measured as 820 Hz.
(i) Deduce that the length of the horn is about 0.20 m.
(ii) Show that the frequency of the first harmonic is about 410 Hz.[5]
(ii) The train approaches a stationary observer at a constant velocity of 50ms–1 and sounds its horn at the same frequency as in (a)(ii). Calculate the frequency of the sound as measured by the observer.[4]
▶️Answer/Explanation
Markscheme
a.
(i) \({f_1} = \frac{v}{{4L}}\), \({f_2} = 3{f_1} = \frac{{3v}}{{4L}}\);
\({f_2} – {f_1} = \frac{v}{{2L}} = 820\left( {{\rm{Hz}}} \right)\);
\(L = \frac{{330}}{{2 \times 820}}\);
(L=0.20m)
(ii) \(\lambda = 4L = 0.80\left( {\rm{m}} \right)\);
\(f = \left( {\frac{{330}}{{0.8}}} \right) = 413 {\rm{Hz}}\);
This is a question testing units for this option. Do not award second marking point for an incorrect or missing unit.
(i) a change in the observed frequency/wavelength of a wave;
when there is relative motion of observer and source;
(ii) \(f’\left( { = f\frac{v}{{v – {u_s}}}} \right) = 410 \times \frac{{330}}{{330 – 50}}\);
\(f’ = 480\left( {{\rm{Hz}}} \right)\);
Allow ECF from (a)(ii).
