IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.5
Topic 9 Weightage : 5 %
All Questions for Topic 9.5 – The Doppler effect for sound waves and light waves
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
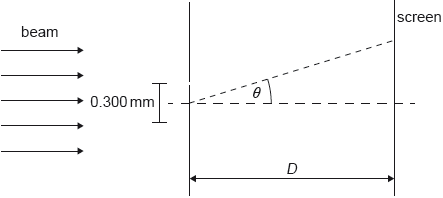
The graph of variation of intensity with diffraction angle for this experiment is shown.
a.ii.
Outline why the beam has to be coherent in order for the fringes to be visible.[1]
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.[3]
Deduce, in mm, the width of one slit.[2]
The wavelength of the light in the beam when emitted by the galaxy was 621.4 nm.
Explain, without further calculation, what can be deduced about the relative motion of the galaxy and the Earth.[2]
▶️Answer/Explanation
Markscheme
a.ii.
light waves (from slits) must have constant phase difference / no phase difference / be in phase
OWTTE
[1 mark]
sin θ = \(\frac{{4 \times 633.0 \times {{10}^{ – 9}}}}{{0.300 \times {{10}^{ – 3}}}}\)
sin θ = 0.0084401…
final answer to three sig figs (eg 0.00844 or 8.44 × 10–3)
Allow ECF from (a)(iii).
Award [1] for 0.121 rad (can award MP3 in addition for proper sig fig)
Accept calculation in degrees leading to 0.481 degrees.
Award MP3 for any answer expressed to 3sf.
[3 marks]
use of diffraction formula «b = \(\frac{\lambda }{\theta }\)»
OR
\(\frac{{633.0 \times {{10}^{ – 9}}}}{{0.00844}}\)
«=» 7.5«00» × 10–2 «mm»
Allow ECF from (b)(i).
[2 marks]
wavelength increases (so frequency decreases) / light is redshifted
galaxy is moving away from Earth
Allow ECF for MP2 (ie wavelength decreases so moving towards).
[2 marks]
a.
Police use radar to detect speeding cars. A police officer stands at the side of the road and points a radar device at an approaching car. The device emits microwaves which reflect off the car and return to the device. A change in frequency between the emitted and received microwaves is measured at the radar device.
The frequency change Δf is given by
\[\Delta f = \frac{{2fv}}{c}\]
where f is the transmitter frequency, v is the speed of the car and c is the wave speed.
The following data are available.
| Transmitter frequency f | = 40 GHz |
| Δf | = 9.5 kHz |
| Maximum speed allowed | = 28 m s–1 |
(i) Explain the reason for the frequency change.
(ii) Suggest why there is a factor of 2 in the frequency-change equation.
(iii) Determine whether the speed of the car is below the maximum speed allowed.[6]
Airports use radar to track the position of aircraft. The waves are reflected from the aircraft and detected by a large circular receiver. The receiver must be able to resolve the radar images of two aircraft flying close to each other.
The following data are available.
| Diameter of circular radar receiver | = 9.3 m |
| Wavelength of radar | = 2.5 cm |
| Distance of two aircraft from the airport | = 31 km |
Calculate the minimum distance between the two aircraft when their images can just be resolved.[2]
▶️Answer/Explanation
Markscheme
a.
i
mention of Doppler effect
OR
«relative» motion between source and observer produces frequency/wavelength change
Accept answers which refer to a double frequency shift.
Award [0] if there is any suggestion that the wave speed is changed in the process.
the reflected waves come from an approaching “source”
OR
the incident waves strike an approaching “observer”
increased frequency received «by the device or by the car»
ii
the car is a moving “observer” and then a moving “source”, so the Doppler effect occurs twice
OR
the reflected radar appears to come from a “virtual image” of the device travelling at 2 v towards the device
iii
ALTERNATIVE 1
For both alternatives, allow ecf to conclusion if v OR Δf are incorrectly calculated.
v = «\(\frac{{\left( {3 \times {{10}^8}} \right) \times \left( {9.5 \times {{10}^3}} \right)}}{{\left( {40 \times {{10}^9}} \right) \times 2}} = \)» 36 «ms–1»
«36> 28» so car exceeded limit
There must be a sense of a conclusion even if numbers are not quoted.
ALTERNATIVE 2
reverse argument using speed limit.
\(\Delta f = \) «\(\frac{{2 \times 40 \times {{10}^9} \times 28}}{{3 \times {{10}^8}}} = \)» 7500 «Hz»
« 9500> 7500» so car exceeded limit
There must be a sense of a conclusion even if numbers are not quoted.
\(x = \frac{{31 \times {{10}^3} \times 1.22 \times 2.5 \times {{10}^{ – 2}}}}{{9.3}}\)
Award [2] for a bald correct answer.
Award [1 max] for POT error.
100 «m»
Award [1 max] for 83m (omits 1.22).
