IBDP Physics- A.1 Kinematics- IB Style Questions For HL Paper 1A -FA 2025
Question
(B) The rate at which an object’s position changes
(C) Total distance traveled divided by total time taken
(D) The rate at which an object’s distance from a point changes
▶️ Answer/Explanation
Instantaneous velocity is defined as the rate of change of position with respect to time at a specific instant.
Option (A) defines average velocity, (C) defines average speed, and (D) refers to the rate of change of distance (speed), not velocity.
✅ Answer: (B)
Question
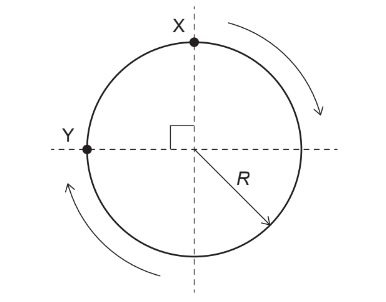
(B) \( R \dfrac{\pi}{2} \)
(C) \( R\sqrt{2} \)
(D) \( R \)
▶️ Answer/Explanation
Displacement is defined as the straight-line distance between the initial and final positions, independent of the path taken.
Points \(X\) and \(Y\) lie on the circumference of the circle and are separated by a quarter turn, so the displacement is the chord joining \(X\) and \(Y\).
The chord subtends an angle of \(90^\circ\) at the center of the circle. Using geometry, the length of the chord is \[ \sqrt{R^2 + R^2} = R\sqrt{2}. \]
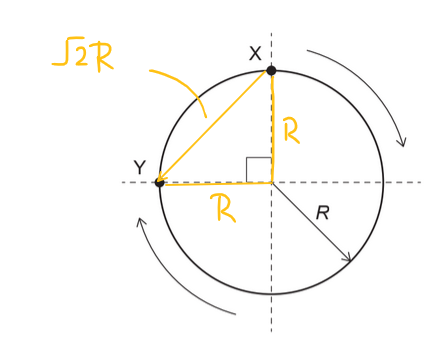
✅ Answer: (C)
Question
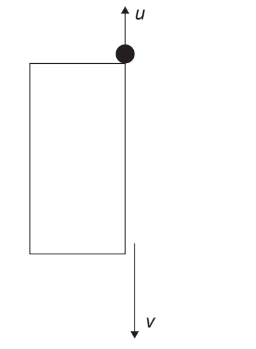
A stone of mass \(m\) is projected vertically upwards with speed \(u\) from the top of a cliff. The speed of the stone just before it reaches the ground is \(v\).
What is the magnitude of the change in momentum of the stone?
(B) \( m\left(\dfrac{v-u}{2}\right) \)
(C) \( m(v+u) \)
(D) \( m(v-u) \)
▶️ Answer/Explanation
Take the upward direction as positive.
Initial momentum of the stone is \(p_{\text{initial}} = +mu\).
Final momentum of the stone just before hitting the ground is \(p_{\text{final}} = -mv\).
The change in momentum is given by \(\Delta p = p_{\text{final}} – p_{\text{initial}}\).
Substituting values, \(\Delta p = (-mv) – (mu) = -m(v + u)\).
Therefore, the magnitude of the change in momentum is \(|\Delta p| = m(v + u)\).
✅ Answer: (C)
