IBDP Physics- A.4 Rigid body mechanics- IB Style Questions For HL Paper 1A -FA 2025
Question
(B) \( 4I\sqrt{\pi\alpha} \)
(C) \( 2I\sqrt{2\alpha} \)
(D) \( 4I\sqrt{\alpha} \)
▶️ Answer/Explanation
Change in angular momentum \( \Delta L = I\Delta\omega \)
Using rotational kinematics: \( \omega^2 = \omega_0^2 + 2\alpha\theta \)
Since it starts from rest: \( \omega = \sqrt{2\alpha\theta} \)
Angular displacement: \( \theta = 4 \times 2\pi = 8\pi \, \text{rad} \)
\( \omega = \sqrt{2\alpha \times 8\pi} = \sqrt{16\pi\alpha} = 4\sqrt{\pi\alpha} \)
\( \Delta L = I \times 4\sqrt{\pi\alpha} = 4I\sqrt{\pi\alpha} \)
✅ Answer: (B)
Question
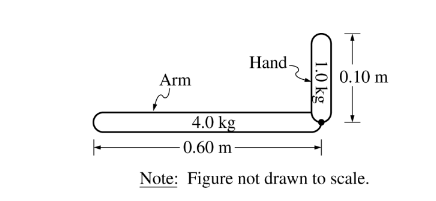
The arm is held in a horizontal position and the hand is bent at the wrist so that the fingers point upward, as shown in the figure.
The torque exerted by the weight of the hand with respect to the shoulder is most nearly
(B) \(10\,\text{N m}\)
(C) \(30\,\text{N m}\)
(D) \(60\,\text{N m}\)
(E) \(70\,\text{N m}\)
▶️ Answer/Explanation
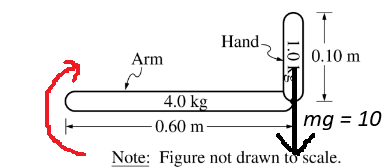
The magnitude of the torque is given by \( \tau = r F \sin \theta \), where \( r \) is the perpendicular distance from the shoulder to the point of application of the force, \( F \) is the weight of the hand, and \( \theta \) is the angle between \( r \) and \( F \).
The force due to the weight of the hand is \( F = mg = (1.0)(9.8) = 9.8\,\text{N} \).
The perpendicular distance from the shoulder is approximately \( r = 0.60\,\text{m} \), and the angle between \( r \) and \( F \) is \(90^\circ\).
Therefore, \( \tau = (0.60)(9.8)\sin 90^\circ = (0.60)(9.8) = 5.88\,\text{N m} \).
This is closest to \(6\,\text{N m}\).
✅ Answer: (A)
Question
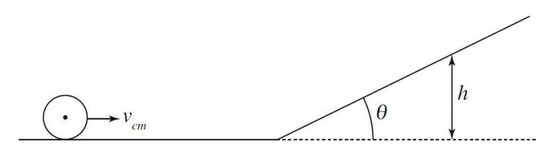
The center of mass of a cylinder of mass \(m\), radius \(r\), and rotational inertia \(I=\tfrac{1}{2}mr^2\) has a velocity of \(v_{cm}\) as it rolls without slipping along a horizontal surface. It then encounters a ramp of angle \(\theta\), and continues to roll up the ramp without slipping.
What is the maximum height the cylinder reaches?
(B) \( \dfrac{4v^2}{3g} \)
(C) \( \dfrac{v^2}{3g} \)
(D) \( \dfrac{3v^2}{4g} \)
(E) \( \dfrac{4g}{3v^2} \)
▶️ Answer/Explanation
Use conservation of mechanical energy.
Initial energy (rolling without slipping) is the sum of translational and rotational kinetic energies:
\(K_T=\tfrac{1}{2}mv_{cm}^2\), and \(K_R=\tfrac{1}{2}I\omega^2\).
For rolling without slipping, \(v_{cm}=\omega r\) so \(\omega=\dfrac{v_{cm}}{r}\).
At the maximum height, the cylinder momentarily comes to rest, so all kinetic energy becomes gravitational potential energy \(mgh\):
\(\tfrac{1}{2}mv_{cm}^2+\tfrac{1}{2}I\omega^2=mgh\).
Substitute \(I=\tfrac{1}{2}mr^2\) and \(\omega=\dfrac{v_{cm}}{r}\):
\(\tfrac{1}{2}mv_{cm}^2+\tfrac{1}{2}\left(\tfrac{1}{2}mr^2\right)\left(\dfrac{v_{cm}}{r}\right)^2=mgh\).
\(\tfrac{1}{2}mv_{cm}^2+\tfrac{1}{4}mv_{cm}^2=mgh\).
\(\tfrac{3}{4}mv_{cm}^2=mgh\).
Therefore \(h=\dfrac{3v_{cm}^2}{4g}\), which corresponds to option (D).
✅ Answer: (D)
