IBDP Physics- A.4 Rigid body mechanics HL- IB Style Questions For HL Paper 2 -FA 2025

(a)
The coefficient of friction (μ) is defined as the ratio \( μ = \frac{F_f}{F_N} \), where \( F_f \) is the frictional force and \( F_N \) is the normal force. Since both forces have the same units, they cancel out, making μ dimensionless.
\(\boxed{\text{Ratio of two forces with same units, units cancel}}\)

(b)
The minimum force to overcome static friction is \( F_{\text{min}} = μ_s mg \):
\( F_{\text{min}} = 0.36 × 1.2 × 9.8 = 4.2336 \, \text{N} ≈ 4.2 \, \text{N} \) ≈ 4 N.
\(\boxed{F ≈ 4.2 \, \text{N}}\)

(c)
During the push: Net force = \( 14.0 – (0.28 × 1.2 × 9.8) = 14.0 – 3.2928 = 10.7072 \, \text{N} \)
Work done = \( 10.7072 × 0.35 = 3.7475 \, \text{J} \)
This equals kinetic energy gained.
After push: friction force = \( 3.2928 \, \text{N} \)
Using work-energy: \( 3.2928 × d = 3.7475 \) ⇒ \( d ≈ 1.14 \, \text{m} \)
\(\boxed{d ≈ 1.14 \, \text{m}}\)

(d)
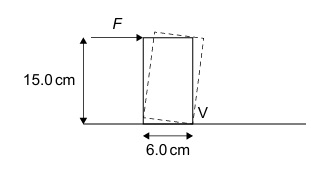
(i) Taking moments about V:
Clockwise: \( F × 0.15 \)
Anticlockwise: \( 1.2 × 9.8 × 0.03 \)
Equate: \( F = \frac{1.2 × 9.8 × 0.03}{0.15} ≈ 2.4 \, \text{N} \)
\(\boxed{F ≈ 2.4 \, \text{N}}\)

(ii) The applied horizontal force F (≈2.4 N) is less than the maximum static friction force \( μ_s mg \) (≈4.2 N), so sliding does not occur.
\(\boxed{F < μ_s mg}\)