Home / IBDP Physics- C.3 Wave phenomena- IB Style Questions For SL Paper 2

IBDP Physics- C.3 Wave phenomena- IB Style Questions For SL Paper 2 -FA 2025

IBDP Physics SL Paper 2 -FA 2025- All Chapters

Question

(a) One distinction between sound waves and electromagnetic waves is that sound waves are longitudinal whereas electromagnetic waves are transverse. State one other difference between sound waves and electromagnetic waves.
A loudspeaker is positioned at point L above the surface of water. A sound detector is located at point D at the same height above the water surface as L. The sound reaches D by two paths: a direct path LD and a reflected path LPD.
The following data are provided:
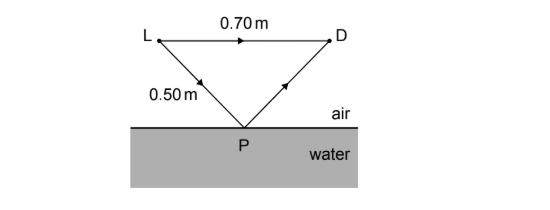
Frequency of the sound wave \(= 1700\,Hz\)
Speed of sound in air \(= 340\,m\,s^{-1}\)
Speed of sound in water \(= 1500\,m\,s^{-1}\)
Distance \(LD = 0.70\,m\)
Distance \(LP = 0.50\,m\)
(b) (i) Calculate the wavelength of the sound wave in air.
(ii) Explain why the sound arriving at D from L undergoes destructive interference.
(c) Predict whether the sound wave is able to enter the water at point P.

Most-appropriate topic codes (IB Physics):

• Topic C.2: Wave model (Properties of waves) — part (a)
• Topic C.3: Wave phenomena (Interference, Refraction) — part (b), (c)
▶️ Answer/Explanation
Detailed solution

(a)
Sound waves require a medium to propagate (mechanical waves), whereas electromagnetic waves can propagate in a vacuum. Alternatively, the speed of sound is much lower than the speed of electromagnetic waves.

(b)
(i) \(\lambda = \frac{v}{f} = \frac{340}{1700} = 0.20\,m\).
(ii) Calculate path difference: Path LPD \(= 0.50 + 0.50 = 1.00\,m\). Path LD \(= 0.70\,m\).
Path difference \(= 1.00 – 0.70 = 0.30\,m\).
Phase difference in wavelengths: \(\frac{0.30}{0.20} = 1.5\lambda\).
Since the path difference is \((n + 0.5)\lambda\) (specifically \(1.5\lambda\)), the waves meet out of phase, causing destructive interference.

(c)
Calculate the angle of incidence \(\theta_1\). From geometry, \(\sin \theta_1 = \frac{0.35}{0.50} = 0.70\) (\(\theta_1 \approx 44^\circ\)).
Check for refraction using Snell’s Law: \(\frac{\sin \theta_1}{v_1} = \frac{\sin \theta_2}{v_2}\).
\(\sin \theta_2 = \frac{1500}{340} \times 0.70 \approx 3.1\).
Since \(\sin \theta_2 > 1\), refraction is not possible. Total internal reflection occurs, so the sound cannot enter the water.

More C.3 Wave phenomena SL Paper 2 SL Paper 2 Questions..
Scroll to Top