IBDP Physics- C.4 Standing waves and resonance- IB Style Questions For SL Paper 2 -FA 2025
Question
(ii) Suggest how conservation of energy is consistent with the fact that the energy at \(P_1\) and \(P_2\) is zero.
Most-appropriate topic codes (IB Physics 2025):
• C.4: Standing waves and resonance — implicit in interference context
▶️ Answer/Explanation
(a)
Light comes from a single source ✓
Waves need to have a constant phase difference / be in phase ✓
To produce a fixed/stable/clear/constant pattern over time ✓
OR
Only coherent light has this property/produces this pattern ✓
(b)(i)
Alternative 1:
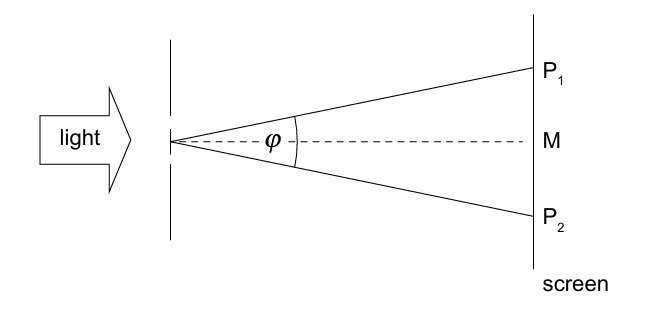
Using the formula for fringe separation: \( s = \frac{\lambda D}{d} \) and angular separation \( \phi = \frac{s}{D} \)
\( \phi = \frac{\lambda}{d} = \frac{720 \times 10^{-9}}{0.12 \times 10^{-3}} = 6.0 \times 10^{-3} \ \text{rad} \quad \checkmark \)
Alternative 2:
For first minima: \( d \sin\!\left(\frac{\phi}{2}\right) = \frac{\lambda}{2} \)
\( \phi = 2 \sin^{-1}\!\left(\frac{\lambda}{2d}\right) = 2 \sin^{-1}\!\left(\frac{720 \times 10^{-9}}{2 \times 0.12 \times 10^{-3}}\right) \approx 6.0 \times 10^{-3} \ \text{rad} \quad \checkmark \)
Alternative 3:
Using the small-angle approximation: \( d \cdot \frac{\phi}{2} = \frac{\lambda}{2} \)
\( \phi = \frac{\lambda}{d} = \frac{720 \times 10^{-9}}{0.12 \times 10^{-3}} = 6.0 \times 10^{-3} \ \text{rad} \quad \checkmark \)
(b)(ii)
The energy absent at \(P_1\) and \(P_2\) is redistributed to the maxima ✓
Energy is conserved: it is transferred from regions of destructive interference to regions of constructive interference.