Home / IBDP Physics- D.2 Electric and magnetic fields- IB Style Questions For HL Paper 2

IBDP Physics- D.2 Electric and magnetic fields- IB Style Questions For HL Paper 2 -FA 2025

IBDP Physics HL Paper 2 -FA 2025- All Chapters

Question

An electron starts from rest and is accelerated through an electric potential difference \(V\). After acceleration, the electron has a speed of \(9.4 \times 10^{6}\,m\,s^{-1}\).
(a) Calculate the value of \(V\).
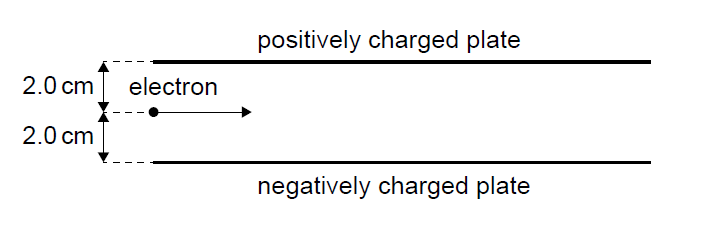
The electron then enters a region containing a uniform electric field between two parallel charged plates. Initially, the electron is located midway between the plates and its velocity is directed parallel to them.
The following information is provided:
Initial speed of the electron \(= 9.4 \times 10^{6}\,m\,s^{-1}\)
Potential difference across the plates \(= 30\,V\)
Separation of the plates \(= 4.0\,cm\)
(b) (i) State the direction of the electron’s acceleration.
(ii) Show that the magnitude of the acceleration of the electron is approximately \(10^{14}\,m\,s^{-2}\).
(c) The electron strikes one of the plates. Determine the distance travelled by the electron in the direction parallel to the plates.
In a separate experiment, a uniform magnetic field directed into the plane of the page is applied between the plates. The electron passes straight through the combined electric and magnetic fields without deflection.
(d) Calculate the strength of the magnetic field.

Most-appropriate topic codes (IB Physics):

• Topic D.2: Electric and magnetic fields (motion of charged particles) — parts (a), (b), (c)
• Topic D.3: Motion in electromagnetic fields (velocity selector) — part (d)
▶️ Answer/Explanation
Detailed solution

(a)
Using energy conservation, \[ \tfrac{1}{2}mv^2 = eV \] \[ V = \frac{0.5 \times 9.11 \times 10^{-31} \times (9.4 \times 10^6)^2}{1.60 \times 10^{-19}} \approx 2.5 \times 10^{2}\,V. \]

(b)
(i) The electron accelerates upwards, towards the positively charged plate.
(ii) The electric field strength is \[ E = \frac{V}{d} = \frac{30}{0.04} = 750\,V\,m^{-1}. \] The force on the electron is \[ F = qE = 1.60 \times 10^{-19} \times 750 = 1.2 \times 10^{-16}\,N. \] Hence, \[ a = \frac{F}{m} \approx \frac{1.2 \times 10^{-16}}{9.11 \times 10^{-31}} \approx 1.3 \times 10^{14}\,m\,s^{-2}. \]

(c)
The electron begins midway between the plates, so the vertical distance travelled is \(0.02\,m\). Using \[ s = \tfrac{1}{2}at^2 \] gives \[ t \approx 1.7 \times 10^{-8}\,s. \] The horizontal distance travelled is \[ x = vt \approx 9.4 \times 10^6 \times 1.7 \times 10^{-8} \approx 0.16\,m. \]

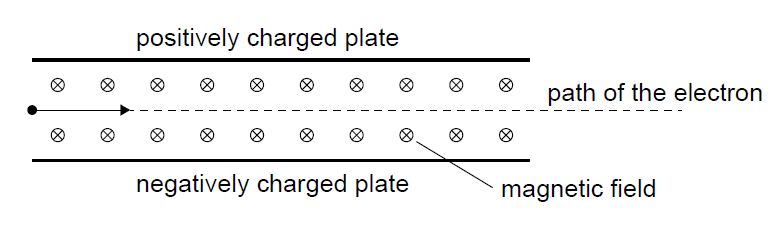
(d)
For no deflection, \[ qE = qvB. \] Therefore, \[ B = \frac{E}{v} = \frac{750}{9.4 \times 10^6} \approx 8.0 \times 10^{-5}\,T. \]

More DP Physics HL Paper 2 Questions..
Scroll to Top