Home / IBDP Physics- D.3 Motion in electromagnetic fields- IB Style Questions For SL Paper 1A

IBDP Physics- D.3 Motion in electromagnetic fields- IB Style Questions For SL Paper 1A -FA 2025

IBDP Physics SL Paper 1 -FA 2025- All Chapters

Question

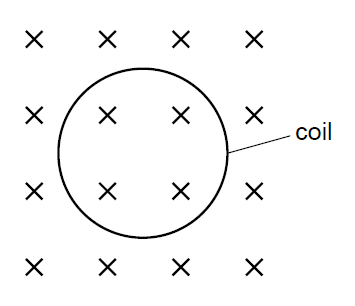
A circular coil lies in the plane of the page and is placed in a uniform magnetic field directed into the page. Negative charge carriers move around the coil in a counter-clockwise direction. What magnetic effect does this produce on the coil?
(A) The coil will rotate clockwise in the plane of the paper.
(B) The coil will rotate counter-clockwise in the plane of the paper.
(C) The diameter of the coil will tend to increase.
(D) The diameter of the coil will tend to decrease.
▶️ Answer/Explanation
Detailed solution

1. Determine Conventional Current:
Negative charge carriers (electrons) move counter-clockwise. Conventional current is defined as the direction of positive charge flow, so it is clockwise.

2. Apply the Motor (Left-Hand) Rule:

  • Magnetic field (B): Into the page.
  • Current (I): Clockwise.
    • Top of the loop (current to the right): force acts upward.
    • Bottom of the loop (current to the left): force acts downward.
    • Left side of the loop (current upward): force acts to the left.
    • Right side of the loop (current downward): force acts to the right.

3. Conclusion:
The magnetic forces act radially outward on all sections of the coil. As a result, the coil tends to expand and its diameter increases.
✅ Answer: (C)

Question

An electron enters a region of uniform magnetic field at a speed \(v\). The direction of the electron is perpendicular to the magnetic field. The path of the electron inside the magnetic field is circular with radius \(r\).
D.3 Motion in electromagnetic fields SL Paper 1
The speed of the electron is varied to obtain different values of \(r\).
Which graph represents the variation of speed \(v\) with \(r\)?
D.3 Motion in electromagnetic fields SL Paper 1
▶️ Answer/Explanation
Detailed solution

With \(v\) perpendicular to \(B\), the magnetic force provides the centripetal force.
Magnetic force magnitude: \(F_{\text{mag}} = qvB\).
Centripetal force: \(F_{\text{cent}} = \dfrac{mv^{2}}{r}\).

Equate them: \(qvB = \dfrac{mv^{2}}{r}\).
Cancel one \(v\): \(qB = \dfrac{mv}{r}\).
So \(v = \dfrac{qB}{m}\,r\).

Therefore \(v\) is directly proportional to \(r\): a straight line through the origin.

✅ Answer: (A)

Question

An electron is accelerated from rest through a potential difference \(V\).
What is the maximum speed of the electron?
(A) \(\sqrt{\frac{2eV}{m_e}}\)
(B) \(\frac{eV}{m_e}\)
(C) \(\frac{2eV}{m_\theta}\)
(D) \(\sqrt{\frac{2V}{m_e}}\)
▶️ Answer/Explanation
Detailed solution

The work done on a charge \(e\) moved through a potential difference \(V\) is \(W = eV\).
Starting from rest, this work becomes the electron’s kinetic energy:
\(\displaystyle eV = \frac{1}{2}m_e v^2\).

Solve for \(v\):
\(\displaystyle v = \sqrt{\frac{2eV}{m_e}}\).

✅ Answer: (A)

More -D. 3 Motion in electromagnetic fields SL Paper 1 Questions..
Scroll to Top