IBDP Physics- D.3 Motion in electromagnetic fields- IB Style Questions For SL Paper 2 -FA 2025
Question
This question is about motion in a magnetic field.
An electron, that has been accelerated from rest by a potential difference of \(250\ \mathrm{V}\), enters a region of magnetic field of strength \(0.12\ \mathrm{T}\) that is directed into the plane of the page.

(a) The electron’s path while in the region of magnetic field is a quarter circle. Show that the
(i) speed of the electron after acceleration is \(9.4 \times 10^{6}\ \mathrm{m\,s^{-1}}\).
(ii) radius of the path is \(4.5 \times 10^{-4}\ \mathrm{m}\).
(ii) radius of the path is \(4.5 \times 10^{-4}\ \mathrm{m}\).
[4]
(b) The diagram below shows the momentum of the electron as it enters and leaves the region of magnetic field. The magnitude of the initial momentum and of the final momentum is \(8.6 \times 10^{-24}\ \mathrm{N\,s}\).

(i) On the diagram above, draw an arrow to indicate the vector representing the change in the momentum of the electron.
(ii) Show that the magnitude of the change in the momentum of the electron is \(1.2 \times 10^{-23}\ \mathrm{N\,s}\).
(iii) The time the electron spends in the region of magnetic field is \(7.5 \times 10^{-11}\ \mathrm{s}\). Estimate the magnitude of the average force on the electron.[3]
Most-appropriate topic codes (IB Physics 2025):
• D.3: Motion in electromagnetic fields
• D.3: Motion in electromagnetic fields
▶️ Answer/Explanation
(a)(i)
\(eV = \dfrac{1}{2}mv^{2}\)
\(v = \sqrt{\dfrac{2eV}{m}}\)
\(v = \sqrt{\dfrac{2 \times 1.6 \times 10^{-19} \times 250}{9.1 \times 10^{-31}}}\)
\(v = 9.4 \times 10^{6}\ \mathrm{m\,s^{-1}}\)
\(eV = \dfrac{1}{2}mv^{2}\)
\(v = \sqrt{\dfrac{2eV}{m}}\)
\(v = \sqrt{\dfrac{2 \times 1.6 \times 10^{-19} \times 250}{9.1 \times 10^{-31}}}\)
\(v = 9.4 \times 10^{6}\ \mathrm{m\,s^{-1}}\)
(a)(ii)
Magnetic force provides centripetal force:
\(evB = \dfrac{mv^{2}}{r}\)
\(r = \dfrac{mv}{eB}\)
\(r = \dfrac{9.1 \times 10^{-31} \times 9.4 \times 10^{6}}{1.6 \times 10^{-19} \times 0.12}\)
\(r = 4.5 \times 10^{-4}\ \mathrm{m}\)
Magnetic force provides centripetal force:
\(evB = \dfrac{mv^{2}}{r}\)
\(r = \dfrac{mv}{eB}\)
\(r = \dfrac{9.1 \times 10^{-31} \times 9.4 \times 10^{6}}{1.6 \times 10^{-19} \times 0.12}\)
\(r = 4.5 \times 10^{-4}\ \mathrm{m}\)
(b)(i)
The change in momentum is represented by the vector joining the tips of the initial and final momentum vectors.
The change in momentum is represented by the vector joining the tips of the initial and final momentum vectors.
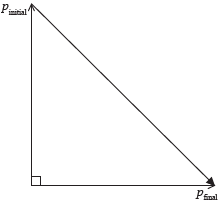
(b)(ii)
The initial and final momentum vectors are perpendicular and equal in magnitude, so
\(\Delta p = \sqrt{p^{2} + p^{2}} = p\sqrt{2}\)
\(\Delta p = 8.6 \times 10^{-24} \times \sqrt{2}\)
\(\Delta p = 1.2 \times 10^{-23}\ \mathrm{N\,s}\)
The initial and final momentum vectors are perpendicular and equal in magnitude, so
\(\Delta p = \sqrt{p^{2} + p^{2}} = p\sqrt{2}\)
\(\Delta p = 8.6 \times 10^{-24} \times \sqrt{2}\)
\(\Delta p = 1.2 \times 10^{-23}\ \mathrm{N\,s}\)
(b)(iii)
\(F_{\text{avg}} = \dfrac{\Delta p}{\Delta t}\)
\(F_{\text{avg}} = \dfrac{1.2 \times 10^{-23}}{7.5 \times 10^{-11}}\)
\(F_{\text{avg}} = 1.6 \times 10^{-13}\ \mathrm{N}\)
\(F_{\text{avg}} = \dfrac{\Delta p}{\Delta t}\)
\(F_{\text{avg}} = \dfrac{1.2 \times 10^{-23}}{7.5 \times 10^{-11}}\)
\(F_{\text{avg}} = 1.6 \times 10^{-13}\ \mathrm{N}\)
