Home / IBDP Physics- E.5 Fusion- IB Style Questions For SL Paper 2

IBDP Physics- E.5 Fusion- IB Style Questions For SL Paper 2 -FA 2025

IBDP Physics SL Paper 2 -FA 2025- All Chapters

Question

(a) Define the term solar constant.
The diagram shows a simplified energy-balance representation of the Earth surface-atmosphere system.
The following data are given:
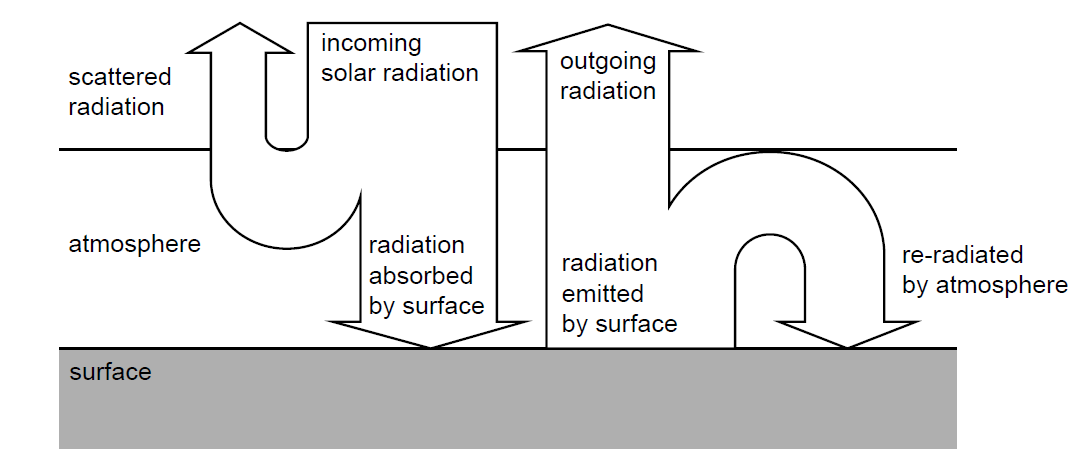
Average albedo of Earth \(= 0.30\)
Average global temperature of the surface \(= 288\,K\)
Average Earth–Sun distance \(= 1.5\times10^{11}\,m\)
(b) (i) Describe the physical process by which some of the radiation emitted by the surface is absorbed by greenhouse gases in the atmosphere and then re-radiated towards the surface.
(ii) Show that the average global intensity of radiation absorbed by the surface is about \(240\,W\,m^{-2}\).
(iii) Determine the average intensity re-radiated by the atmosphere towards the surface. Assume that the emissivity of the surface is \(0.90\).
(c) Using the solar constant, show that the total power radiated by the Sun is about \(4\times10^{26}\,W\).
(d) The Sun’s main energy source is the proton–proton (p–p) fusion chain. The overall reaction is \(4_{1}^{1}p+2_{-1}^{0}e\rightarrow{}_{2}^{4}He+2_{0}^{0}v_{e}+4\gamma\).
(i) The mass of the helium nucleus is \(4.001506\,u\). Calculate, in MeV, the energy released in the reaction.
(ii) Explain how fusion reactions help maintain a stable radius of the Sun.
(iii) Outline how the presence of helium in the Sun can be confirmed empirically.
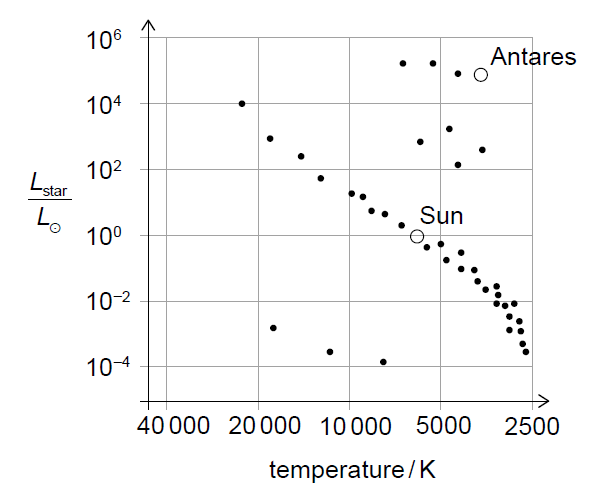
(e) The positions of the Sun and the star Antares are shown in the Hertzsprung–Russell (HR) diagram.

(i) State the classification of Antares.
(ii) Discuss how nuclear fusion processes in Antares differ from those in the Sun.

Most-appropriate topic codes (IB Physics):

• Topic B.2: Greenhouse effect (Energy balance) — part (a), (b)
• Topic B.1: Thermal energy transfers (Black body radiation) — part (b)(iii)
• Topic E.5: Fusion and stars (HR diagram, Stellar evolution) — part (d), (e)
▶️ Answer/Explanation
Detailed solution

(a)
The solar constant is the intensity (power per unit area) of solar radiation received at the top of the Earth’s atmosphere, measured perpendicular to the rays, at the average Earth–Sun distance.

(b)
(i) Greenhouse gas molecules absorb infrared radiation emitted by the surface because the radiation energy matches the difference between molecular energy levels (resonance). The molecules then re-radiate this energy in all directions, including back towards the surface.
(ii) Average incoming intensity \(I_{in} = \frac{S}{4} \approx 340\,W\,m^{-2}\).
Absorbed intensity \(= (1 – \text{albedo}) \times I_{in} = (1 – 0.30) \times 340 = 238\,W\,m^{-2}\) (approx \(240\)).
(iii) At the surface: Energy In = Energy Out.
Absorbed Solar + Re-radiated from Atmosphere = Emitted by Surface.
Emitted by surface \(I_{emit} = \epsilon \sigma T^4 = 0.90 \times 5.67 \times 10^{-8} \times (288)^4 \approx 351\,W\,m^{-2}\).
\(238 + I_{atm} = 351 \implies I_{atm} = 113\,W\,m^{-2}\).

(c)
Using \(S \approx 1360\,W\,m^{-2}\) and \(d = 1.5 \times 10^{11}\,m\):
\(P = S \times 4\pi d^2 \approx 3.8 \times 10^{26}\,W\).

(d)
(i) \(\Delta m = [4(1.007276) + 2(0.000549)] – 4.001506 = 0.028696\,u\).
Energy \(Q = 0.028696 \times 931.5\,MeV \approx 26.7\,MeV\).
(ii) Fusion releases energy which creates outward radiation pressure. This pressure balances the inward gravitational pull, preventing collapse and maintaining a stable radius.
(iii) By analysing the Sun’s absorption spectrum (Fraunhofer lines), characteristic lines corresponding to helium can be identified.

(e)
(i) Red supergiant.
(ii) The Sun fuses hydrogen into helium, whereas Antares, being a supergiant, has much higher core temperatures and pressures, allowing fusion of heavier elements.

More E.5 Fusion SL Paper 2 Questions..
Scroll to Top