Rocket A and rocket B are travelling in opposite directions from the Earth along the same straight line.
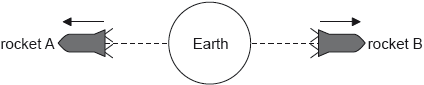
In the reference frame of the Earth, the speed of rocket A is 0.75c and the speed of rocket B is 0.50c.
a.i.Calculate, for the reference frame of rocket A, the speed of rocket B according to the Galilean transformation.[1]
▶️Answer/Explanation
Markscheme
a.i.
1.25c
[1 mark]
ALTERNATIVE 1
\(u’ = \frac{{(0.50 + 0.75)}}{{1 + 0.5 \times 0.75}}c\)
0.91c
ALTERNATIVE 2
\(u’ = \frac{{ – 0.50 – 0.75}}{{1 – ( – 0.5 \times 0.75)}}c\)
–0.91c
[2 marks]
nothing can travel faster than the speed of light (therefore (a)(ii) is the valid answer)
OWTTE
[1 mark]
Muons are created in the upper atmosphere of the Earth at an altitude of 10 km above the surface. The muons travel vertically down at a speed of 0.995c with respect to the Earth. When measured at rest the average lifetime of the muons is 2.1 μs.
a.i.Calculate, according to Galilean relativity, the time taken for a muon to travel to the ground[1]
▶️Answer/Explanation
Markscheme
a.i.
«\(\frac{{{{10}^4}}}{{0.995 \times 3 \times {{10}^8}}} = \)» 34 «μs»
Do not accept 104/c = 33 μs.
[1 mark]
time is much longer than 10 times the average life time «so only a small proportion would not decay»
[1 mark]
\(\gamma = 10\)
\(\Delta {t_0} = \) «\(\frac{{\Delta t}}{\gamma } = \frac{{34}}{{10}} = \)» 3.4 «μs»
[2 marks]
the value found in (b)(i) is of similar magnitude to average life time
significant number of muons are observed on the ground
«therefore this supports the special theory»[2 marks]
The diagram shows the motion of the electrons in a metal wire carrying an electric current as seen by an observer X at rest with respect to the wire. The distance between adjacent positive charges is d.
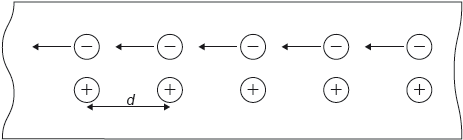
Observer Y is at rest with respect to the electrons.
a.State whether the field around the wire according to observer X is electric, magnetic or a combination of both[1]
▶️Answer/Explanation
Markscheme
a.
magnetic field
[1 mark]
«according to Y» the positive charges are moving «to the right»
d decreases
For MP1, movement of positive charges must be mentioned explicitly.
[2 marks]
positive charges are moving, so there is a magnetic field
the density of positive charges is higher than that of negative charges, so there is an electric field
The reason must be given for each point to be awarded.
[2 marks]
Outline the conclusion from Maxwell’s work on electromagnetism that led to one of the postulates of special relativity.
▶️Answer/Explanation
Markscheme
light is an EM wave
speed of light is independent of the source/observer
a.State one prediction of Maxwell’s theory of electromagnetism that is consistent with special relativity.[1]

A proton is at rest relative to the laboratory and the wire.
Observer X is at rest in the laboratory. Observer Y moves to the right with constant speed relative to the laboratory. Compare and contrast how observer X and observer Y account for any non-gravitational forces on the proton.[3]
▶️Answer/Explanation
Markscheme
a.
the speed of light is a universal constant/invariant
OR
c does not depend on velocity of source/observer
electric and magnetic fields/forces unified/frame of reference dependant
[1 mark]
observer X will measure zero «magnetic or electric» force
observer Y must measure both electric and magnetic forces
which must be equal and opposite so that observer Y also measures zero force
Allow [2 max] for a comment that both X and Y measure zero resultant force even if no valid explanation is given.
[3 marks]
