IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 2 – Mechanics
Topic 2 Weightage : 9%
All Questions for Topic 2 – Distance and displacement , Speed and velocity , Acceleration , Graphs describing motion , Equations of motion for uniform acceleration , Projectile motion , Fluid resistance and terminal speed
This question is about escape speed and gravitational effects.
a
Explain what is meant by escape speed.[2]
Titania is a moon that orbits the planet Uranus. The mass of Titania is 3.5×1021kg. The radius of Titania is 800 km.
(i) Use the data to calculate the gravitational potential at the surface of Titania.
(ii) Use your answer to (b)(i) to determine the escape speed for Titania.[5]
An astronaut visiting Titania throws an object away from him with an initial horizontal velocity of 1.8 m s–1. The object is 1.5 m above the moon’s surface when it is thrown. The gravitational field strength at the surface of Titania is 0.37 N kg–1.
Calculate the distance from the astronaut at which the object first strikes the surface.[3]
▶️Answer/Explanation
Markscheme
a
(minimum) speed of object to escape gravitational field of a planet/travel to infinity;
at surface of planet;
without (further) energy input;
(i) \( – \frac{{6.67 \times {{10}^{ – 11}} \times 3.5 \times {{10}^{21}}}}{{8.0 \times {{10}^5}}}\);
−2.9×105Jkg–1; (allow Nmkg−1)
Award [1 max] if negative sign omitted.
(ii) \(\frac{1}{2}m{v^2} = mV\);
speed=\( = \sqrt {2 \times 2.9 \times {{10}^5}} \); (allow ECF from (b)(i))
7.6 ×102ms-1;
Ignore sign.
Award [3] for a bald correct answer.
time to hit surface \( = \sqrt {\frac{{2.0 \times 1.5}}{{0.37}}} \left( { = 2.85{\rm{s}}} \right)\);
distance to impact = 2.85×1.8;
5.1m;
This question is about the energy of an orbiting satellite.
A space shuttle of mass m is launched in the direction of the Earth’s South Pole.
The shuttle enters a circular orbit of radius \(R\) around the Earth.
a
The kinetic energy \({E_{\text{K}}}\) given to the shuttle at its launch is given by the expression
\[{E_{\text{K}}} = \frac{{7GMm}}{{8{R_{\text{E}}}}}\]
where \(G\) is the gravitational constant, \(M\) is mass of the Earth and \({R_{\text{E}}}\) is the radius of the Earth. Deduce that the shuttle cannot escape the gravitational field of the Earth.[2]
Show that the total energy of the shuttle in its orbit is given by \( – \frac{{GMm}}{{2R}}\). Air resistance is negligible.[3]
Using the expression for \({E_{\text{K}}}\) in (a) and your answer to (b)(i), determine \(R\) in terms of \({R_{\text{E}}}\).[3]
In practice, the total energy of the shuttle decreases as it collides with air molecules in the upper atmosphere. Outline what happens to the speed of the shuttle when this occurs.[2]
▶️Answer/Explanation
Markscheme
a
KE needs to be \( \ge \) (magnitude of) GPE at surface \(\left( { – \frac{{GMm}}{{{R_E}}}} \right)\);
But KE is \(\frac{{7GMm}}{{8{R_{\text{E}}}}} < \frac{{GMm}}{{{R_{\text{E}}}}}\) / OWTTE;
or
shows that total energy at launch \( = – \frac{{GMm}}{{8{R_{\text{E}}}}}\); (appropriate working required)
this is \( < 0\), so escape impossible;
or
states that escape velocity needed is \(\sqrt {\frac{{2GM}}{{{R_{\text{E}}}}}} \);
shows launch velocity is only \(\sqrt {\frac{{7GM}}{{4{R_{\text{E}}}}}} \); (appropriate working required)
\({E_{{\text{tot}}}} = {\text{PE}} + {\text{KE}}\);
shows that kinetic energy \( = (\frac{1}{2}m{v^2} = ){\text{ }}\frac{{GMm}}{{2R}}\); (appropriate working required)
adds PE \(\left( { – \frac{{GMm}}{R}} \right)\) and KE to get given answer; (appropriate working required)
\( – \frac{{GMm}}{{{R_{\text{E}}}}} + \frac{{7GMm}}{{8{R_{\text{E}}}}} = – \frac{{GMm}}{{2R}}\); (equating total energy at launch and in orbit)
\(\frac{1}{{8{R_{\text{E}}}}} = \frac{1}{{2R}}\);
\(R = 4{R_{\text{E}}}\);
Award [0] for an answer such as \(R = \frac{{4{R_{\text{E}}}}}{7}\).
total energy decreases/becomes a greater negative value, so R decreases;
as \(R\) decreases kinetic energy increases;
speed increases;
Allow third marking point even if reasoning is incorrect.
This question is about the thermodynamics of a car engine and the dynamics of the car.
A car engine consists of four cylinders. In each of the cylinders, a fuel-air mixture explodes to supply power at the appropriate moment in the cycle.
The diagram models the variation of pressure P with volume V for one cycle of the gas, ABCDA, in one of the cylinders of the engine. The gas in the cylinder has a fixed mass and can be assumed to be ideal.
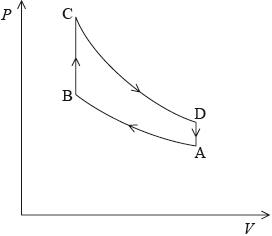
The car is travelling at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\). At this speed, the energy provided by the fuel injected into one cylinder in each cycle is 9200 J. One litre of fuel provides 56 MJ of energy.
A car is travelling along a straight horizontal road at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\). The power output required at the wheels is 0.13 MW.
A driver moves a car in a horizontal circular path of radius 200 m. Each of the four tyres will not grip the road if the frictional force between a tyre and the road becomes less than 1500 N.
a At point A in the cycle, the fuel-air mixture is at 18 °C. During process AB, the gas is compressed to 0.046 of its original volume and the pressure increases by a factor of 40. Calculate the temperature of the gas at point B.[1]
(ii) Each of the four cylinders completes a cycle 18 times every second. Calculate the distance the car can travel on one litre of fuel at a speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\).[3]
(ii) The mass of the car is 1200 kg. The resistive force F is related to the speed v by \(F \propto {v^2}\). Using your answer to (g)(i), determine the maximum theoretical acceleration of the car at a speed of \({\text{28 m}}\,{{\text{s}}^{ – 1}}\).[5]
(ii) While the car is travelling around the circle, the people in the car have the sensation that they are being thrown outwards. Outline how Newton’s first law of motion accounts for this sensation.[6]
▶️Answer/Explanation
Markscheme
a. 535 (K) / 262 (°C);
\(\Delta U = – W\);
as work is done by gas internal energy falls;
temperature falls as temperature is measure of average kinetic energy;
inside the loop / OWTTE;
(ii) one litre \( = \left( {\frac{1}{{4 \times 18 \times 1.64 \times {{10}^{ – 4}}}} = } \right){\text{ }}87{\text{ s of travel}}\);
\((87 \times 56) = 4.7{\text{ (km)}}\);
Allow rounded 1.6 value to be used, giving 4.9 (km).
change in kinetic energy \( = \frac{1}{2} \times {\text{1200}} \times {\text{[2}}{{\text{8}}^2} – {\text{1}}{{\text{2}}^2}]{\text{ (}} = 384{\text{ kJ)}}\);
rate of change in kinetic energy \( = \frac{{{\text{384000}}}}{{{\text{12.5}}}}\); } (allow ECF of 162 from (28 \( – \) 12)2 for this mark)
31 (kW);
or
use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
use of a kinematic equation to determine acceleration \(( = 1.28{\text{ m}}\,{{\text{s}}^{ – 2}})\);
work done \(\frac{{F \times s}}{{{\text{time}}}} = \frac{{1536 \times 250}}{{12.5}}\);
31 (kW);
2300 or 2.3k (N);
Award [2] for a bald correct answer.
(ii) resistive force \( = \frac{{2300}}{4}\)\(\,\,\,\)or\(\,\,\,\)\(\frac{{2321}}{4}{\text{ }}( = {\text{575)}}\); (allow ECF)
so accelerating force \((2300 – 580 = ){\text{ }}1725{\text{ (N)}}\)\(\,\,\,\)or\(\,\,\,\)1741 (N);
\(a = \frac{{1725}}{{1200}} = 1.44{\text{ (m}}\,{{\text{s}}^{ – 2}})\)\(\,\,\,\)or\(\,\,\,\)\(a = \frac{{1741}}{{1200}} = 1.45{\text{ (m}}\,{{\text{s}}^{ – 2}})\);
Award [2 max] for an answer of 0.49 (m\(\,\)s–2 (omits 2300 N).
\({v^2} = F \times \frac{r}{m}\);
\(31.6{\text{ (m}}\,{{\text{s}}^{ – 1}})\);
Allow [3] for a bald correct answer.
Allow [2 max] if 4\( \times \) is omitted, giving 15.8 (m\(\,\)s–1).
(ii) statement of Newton’s first law;
(hence) without car wall/restraint/friction at seat, the people in the car would move in a straight line/at a tangent to circle;
(hence) seat/seat belt/door exerts centripetal force;
(in frame of reference of the people) straight ahead movement is interpreted as “outwards”;
