IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 4.1 Oscillations
Topic 4 Weightage : 5 %
All Questions for Topic Simple harmonic oscillations, Time period, frequency, amplitude, displacement and phase difference , Conditions for simple harmonic motion
The ball is now displaced through a small distance x from the bottom of the bowl and is then released from rest.
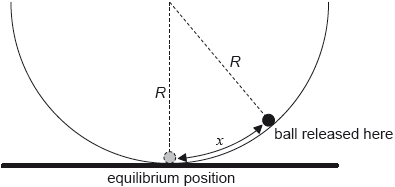
The magnitude of the force on the ball towards the equilibrium position is given by
\[\frac{{mgx}}{R}\]
where R is the radius of the bowl.
d.i. Outline why the ball will perform simple harmonic oscillations about the equilibrium position. [1]
▶️Answer/Explanation
Markscheme
d.i.
the «restoring» force/acceleration is proportional to displacement
Direction is not required
[1 mark]
ω = «\(\sqrt {\frac{g}{R}} \)» = \(\sqrt {\frac{{9.81}}{{8.0}}} \) «= 1.107 s–1»
T = «\(\frac{{2\pi }}{\omega }\) = \(\frac{{2\pi }}{{1.107}}\) =» 5.7 «s»
Allow use of or g = 9.8 or 10
Award [0] for a substitution into T = 2π\(\sqrt {\frac{I}{g}} \)
[2 marks]
sine graph
correct amplitude «0.13 m s–1»
correct period and only 1 period shown
Accept ± sine for shape of the graph. Accept 5.7 s or 6.0 s for the correct period.
Amplitude should be correct to ±\(\frac{1}{2}\) square for MP2
eg: v /m s–1 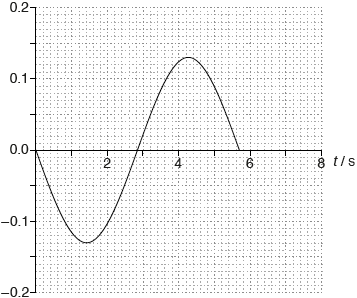
[3 marks]
A buoy, floating in a vertical tube, generates energy from the movement of water waves on the surface of the sea. When the buoy moves up, a cable turns a generator on the sea bed producing power. When the buoy moves down, the cable is wound in by a mechanism in the generator and no power is produced.
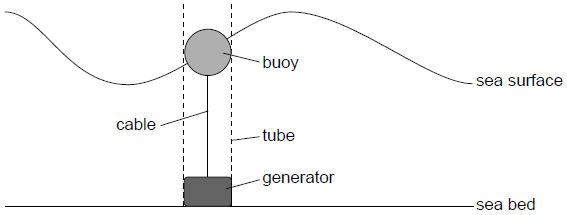
The motion of the buoy can be assumed to be simple harmonic.
Water can be used in other ways to generate energy.
a. Outline the conditions necessary for simple harmonic motion (SHM) to occur.[2]
 [2]
[2]
 [2]
[2]
▶️Answer/Explanation
Markscheme
a.
force/acceleration proportional to displacement «from equilibrium position»
and directed towards equilibrium position/point
OR
and directed in opposite direction to the displacement from equilibrium position/point
Do not award marks for stating the defining equation for SHM.
Award [1 max] for a ω–=2x with a and x defined.
frequency of buoy movement \( = \frac{{3.4}}{{35}}\) or 0.097 «Hz»
OR
time period of buoy \( = \frac{{35}}{{3.4}}\) or 10.3 «s» or 10 «s»
v = «\(\frac{{2\pi {x_0}}}{T}\) or \(2\pi f{x_0}\)» \(\ = \frac{{2 \times \pi \times 4.3}}{{10.3}}\) or \(2 \times \pi \times 0.097 \times 4.3\)
2.6 «m s–1»
peaks separated by gaps equal to width of each pulse «shape of peak roughly as shown»
one cycle taking 10 s shown on graph
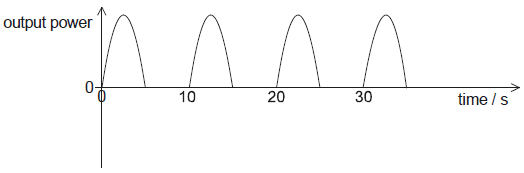
Judge by eye.
Do not accept cos2 or sin2 graph
At least two peaks needed.
Do not allow square waves or asymmetrical shapes.
Allow ECF from (b)(i) value of period if calculated.
PE of water is converted to KE of moving water/turbine to electrical energy «in generator/turbine/dynamo»
idea of pumped storage, ie: pump water back during night/when energy cheap to buy/when energy not in demand/when there is a surplus of energy
specific energy available = «gh =» 9.81 x 270 «= 2650J kg–1»
OR
mgh \( = \frac{1}{2}\)mv2
OR
v2 = 2gh
v = 73 «ms–1»
Do not allow 72 as round from 72.8
total energy = «mgh = 1.5 x 1010 x 9.81 x 270=» 4.0 x 1013 «J»
OR
total energy = «\(\frac{1}{2}m{v^2} = \frac{1}{2} \times 1.5 \times {10^{10}} \times \) (answer (c)(ii))2 =» 4.0 x 1013 «J»
time = «\(\frac{{4.0 \times {{10}^{13}}}}{{4 \times 2.5 \times {{10}^8}}}\)» 11.1h or 4.0 x 104 s
Use of 3.97 x 1013 «J» gives 11 h.
For MP2 the unit must be present.
friction/resistive losses in pipe/fluid resistance/turbulence/turbine or generator «bearings»
OR
sound energy losses from turbine/water in pipe
thermal energy/heat losses in wires/components
water requires kinetic energy to leave system so not all can be transferred
Must see “seat of friction” to award the mark.
Do not allow “friction” bald.
