IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 4.4 Wave behavior
Topic 4 Weightage : 5 %
All Questions for Topic 4.4 – Reflection and refraction , Snell’s law, critical angle and total internal reflection , Diffraction through a single-slit and around objects , Interference patterns , Double-slit interference , Path difference
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
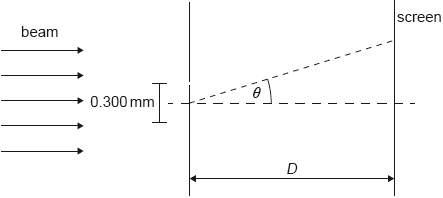
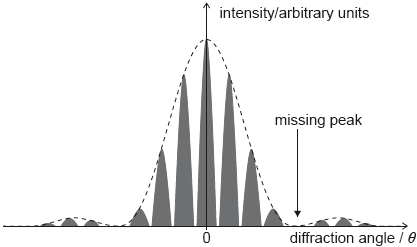
The graph of variation of intensity with diffraction angle for this experiment is shown.
a.ii.
Outline why the beam has to be coherent in order for the fringes to be visible.[1]
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.[3]
Deduce, in mm, the width of one slit.[2]
The wavelength of the light in the beam when emitted by the galaxy was 621.4 nm.
Explain, without further calculation, what can be deduced about the relative motion of the galaxy and the Earth.[2]
▶️Answer/Explanation
Markscheme
a.ii.
light waves (from slits) must have constant phase difference / no phase difference / be in phase
OWTTE[1 mark]
sin θ = \(\frac{{4 \times 633.0 \times {{10}^{ – 9}}}}{{0.300 \times {{10}^{ – 3}}}}\)
sin θ = 0.0084401…
final answer to three sig figs (eg 0.00844 or 8.44 × 10–3)
Allow ECF from (a)(iii).
Award [1] for 0.121 rad (can award MP3 in addition for proper sig fig)
Accept calculation in degrees leading to 0.481 degrees.
Award MP3 for any answer expressed to 3sf.[3 marks]
use of diffraction formula «b = \(\frac{\lambda }{\theta }\)»
OR
\(\frac{{633.0 \times {{10}^{ – 9}}}}{{0.00844}}\)
«=» 7.5«00» × 10–2 «mm»
Allow ECF from (b)(i).[2 marks]
wavelength increases (so frequency decreases) / light is redshifted
galaxy is moving away from Earth
Allow ECF for MP2 (ie wavelength decreases so moving towards).[2 marks]
