IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 6.1 – Circular motion
Topic 6 Weightage : 4 %
All Questions for Topic 6.1 – Period, frequency, angular displacement and angular velocity , Centripetal force , Centripetal acceleration
A satellite powered by solar cells directed towards the Sun is in a polar orbit about the Earth.
The satellite is orbiting the Earth at a distance of 6600 km from the centre of the Earth.
The satellite carries an experiment that measures the peak wavelength emitted by different objects. The Sun emits radiation that has a peak wavelength λS of 509 nm. The peak wavelength λE of the radiation emitted by the Earth is 10.1 μm.
a.
Determine the orbital period for the satellite.
Mass of Earth = 6.0 x 1024 kg[3]
Determine the mean temperature of the Earth.[2]
Suggest how the difference between λS and λE helps to account for the greenhouse effect.[3]
Not all scientists agree that global warming is caused by the activities of man.
Outline how scientists try to ensure agreement on a scientific issue.[1]
▶️Answer/Explanation
Markscheme
a.
\(\frac{{m{v^2}}}{r} = G\frac{{Mm}}{{{r^2}}}\)
leading to T2 = \(\frac{{4{\pi ^2}{r^3}}}{{GM}}\)
T = 5320 «s»
Alternative 2
«\(v = \sqrt {\frac{{G{M_E}}}{r}} \)» = \(\sqrt {\frac{{6.67 \times {{10}^{ – 11}} \times 6.0 \times {{10}^{24}}}}{{6600 \times {{10}^3}}}} \) or 7800 «ms–1»
distance = 2\(\pi \)r = 2\(\pi \) x 6600 x 103 «m» or 4.15 x 107 «m»
«T = \(\frac{d}{v} = \frac{{4.15 \times {{10}^7}}}{{7800}}\)» = 5300 «s»
Accept use of ω instead of v
T = «\(\frac{{2.90 \times {{10}^{ – 3}}}}{{{\lambda _{{\text{max}}}}}} = \)» \(\frac{{2.90 \times {{10}^{ – 3}}}}{{10.1 \times {{10}^{ – 6}}}}\)
= 287 «K» or 14 «°C»
Award [0] for any use of wavelength from Sun
Do not accept 287 °C
wavelength of radiation from the Sun is shorter than that emitted from Earth «and is not absorbed by the atmosphere»
infrared radiation emitted from Earth is absorbed by greenhouse gases in the atmosphere
this radiation is re-emitted in all directions «including back to Earth»
peer review
international collaboration
full details of experiments published so that experiments can repeated[Max 1 Mark]
The diagram below shows part of a downhill ski course which starts at point A, 50 m above level ground. Point B is 20 m above level ground.
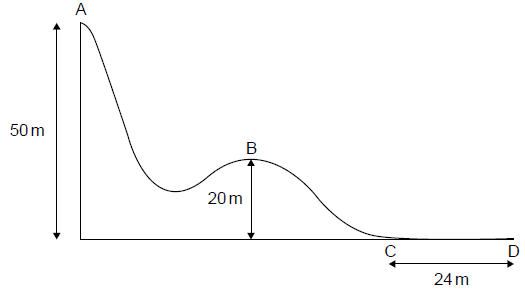
A skier of mass 65 kg starts from rest at point A and during the ski course some of the gravitational potential energy transferred to kinetic energy.
At the side of the course flexible safety nets are used. Another skier of mass 76 kg falls normally into the safety net with speed 9.6 m s–1.
a.i.
From A to B, 24 % of the gravitational potential energy transferred to kinetic energy. Show that the velocity at B is 12 m s–1.[2]
Some of the gravitational potential energy transferred into internal energy of the skis, slightly increasing their temperature. Distinguish between internal energy and temperature.[2]
The dot on the following diagram represents the skier as she passes point B.
Draw and label the vertical forces acting on the skier.
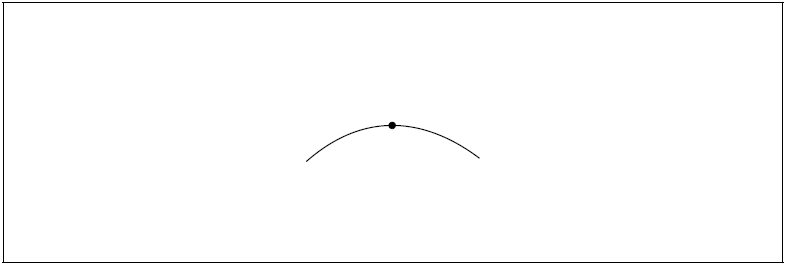 [2]
[2]
The hill at point B has a circular shape with a radius of 20 m. Determine whether the skier will lose contact with the ground at point B.[3]
The skier reaches point C with a speed of 8.2 m s–1. She stops after a distance of 24 m at point D.
Determine the coefficient of dynamic friction between the base of the skis and the snow. Assume that the frictional force is constant and that air resistance can be neglected.[3]
Calculate the impulse required from the net to stop the skier and state an appropriate unit for your answer.[2]
Explain, with reference to change in momentum, why a flexible safety net is less likely to harm the skier than a rigid barrier.[2]
▶️Answer/Explanation
Markscheme
a.i.
\(\frac{1}{2}{v^2} = 0.24\,{\text{gh}}\)
\(v = 11.9\) «m s–1»
Award GPE lost = 65 × 9.81 × 30 = «19130 J»
Must see the 11.9 value for MP2, not simply 12.
Allow g = 9.8 ms–2.
internal energy is the total KE «and PE» of the molecules/particles/atoms in an object
temperature is a measure of the average KE of the molecules/particles/atoms
Award [1 max] if there is no mention of molecules/particles/atoms.
arrow vertically downwards from dot labelled weight/W/mg/gravitational force/Fg/Fgravitational AND arrow vertically upwards from dot labelled reaction force/R/normal contact force/N/FN
W > R
Do not allow gravity.
Do not award MP1 if additional ‘centripetal’ force arrow is added.
Arrows must connect to dot.
Ignore any horizontal arrow labelled friction.
Judge by eye for MP2. Arrows do not have to be correctly labelled or connect to dot for MP2.
ALTERNATIVE 1
recognition that centripetal force is required / \(\frac{{m{v^2}}}{r}\) seen
= 468 «N»
W/640 N (weight) is larger than the centripetal force required, so the skier does not lose contact with the ground
ALTERNATIVE 2
recognition that centripetal acceleration is required / \(\frac{{{v^2}}}{r}\) seen
a = 7.2 «ms–2»
g is larger than the centripetal acceleration required, so the skier does not lose contact with the ground
ALTERNATIVE 3
recognition that to lose contact with the ground centripetal force ≥ weight
calculation that v ≥ 14 «ms–1»
comment that 12 «ms–1» is less than 14 «ms–1» so the skier does not lose contact with the ground
ALTERNATIVE 4
recognition that centripetal force is required / \(\frac{{m{v^2}}}{r}\) seen
calculation that reaction force = 172 «N»
reaction force > 0 so the skier does not lose contact with the ground
Do not award a mark for the bald statement that the skier does not lose contact with the ground.
ALTERNATIVE 1
0 = 8.22 + 2 × a × 24 therefore a = «−»1.40 «m s−2»
friction force = ma = 65 × 1.4 = 91 «N»
coefficient of friction = \(\frac{{91}}{{65 \times 9.81}}\) = 0.14
ALTERNATIVE 2
KE = \(\frac{1}{2}\)mv2 = 0.5 x 65 x 8.22 = 2185 «J»
friction force = KE/distance = 2185/24 = 91 «N»
coefficient of friction = \(\frac{{91}}{{65 \times 9.81}}\) = 0.14
Allow ECF from MP1.
«76 × 9.6»= 730
Ns OR kg ms–1
safety net extends stopping time
F = \(\frac{{\Delta p}}{{\Delta t}}\) therefore F is smaller «with safety net»
OR
force is proportional to rate of change of momentum therefore F is smaller «with safety net»
Accept reverse argument.
