IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 1.2 – Uncertainties and errors
Topic 1 Weightage : 7 %
All Questions for Topic 1.2 – Random and systematic errors , Absolute, fractional and percentage uncertainties , Error bars , Uncertainty of gradient and intercepts
Question
The radius of a circle is measured to be (10.0 ± 0.5)cm. What is the area of the circle?
A. (314.2 ± 0.3) cm2
B. (314 ± 1) cm2
C. (314 ± 15) cm2
D. (314 ± 31) cm2
▶️Answer/Explanation
Ans: D
Radius \( =\left ( 10\pm 0.5 \right )cm \)
Area \( =\pi r^{2} \) \(= 3.14(10)^{2} \) =314 cm
\( \frac{\Delta A}{A}=2\frac{\Delta r}{r} \Delta A=2\times \frac{0.5}{10}\times 314 =\frac{1}{10}\times 314 \Delta A=31.4cm \)
Area \(=\left ( 314\pm 31.4 \right )cm \)
Question
The uncertainty in reading a laboratory thermometer is 0.5°C. The temperature of a liquid falls from 20°C to 10°C as measured by the thermometer. What is the percentage uncertainty in the change in temperature?
A. 2.5%
B. 5%
C. 7.5%
D. 10%
▶️Answer/Explanation
Ans: D
Change in temperature is = 10°c ( 20° to 10°)
Absolute uncertainty \( = 0.5 × 2 \) ( from both values 20°c and 10°c)
% uncertainty \(\frac{\Delta T}{T}\times 100\)
\( \frac{\ 1 }{10}\times 100\)
Percentage uncertainty \(= 10%\)
Question
A pyramid has a square base of side \(x\) and height \(h\). The volume \(V\) of the pyramid is given by the expression:
\[
V=\frac{x^2 h}{3}
\]
If \(V\) is measured to \(5 \%\) and \(h\) is measured to \(3 \%\), what is the percentage uncertainty of \(x\) ? Remember to include the \(\%\) symbol with your answer.
▶️Answer/Explanation
Ans: D
Solution: Since \(V=\frac{x^2 h}{3}\)\[
\Rightarrow x=\sqrt{\frac{3 v}{h}}
\]
so
\[
\left(\frac{\Delta x}{x} \times 100\right)=\frac{1}{2}\left[\left(\frac{\Delta v}{v} \times 100\right)+\left(\frac{\Delta h}{h} \times 100\right)\right]
\]
or
\[
\begin{aligned}
& \left(\frac{\Delta x}{x} \times 100\right)=\frac{1}{2}[5 \%+3 \%] \\
& \left(\frac{\Delta x}{x} \times 100\right)=4 \%
\end{aligned}
\]
Question
A proton has momentum 10–20 N s and the uncertainty in the position of the proton is 10–10 m.
What is the minimum fractional uncertainty in the momentum of this proton?
A. 5 × 10–25
B. 5 × 10–15
C. 5 × 10–5
D. 2 × 104
▶️Answer/Explanation
Ans: C
\(\Delta X .\Delta P= \frac{h}{4\Pi }\)
\(10^{-10}.\Delta P=\frac{6.63\times 10^{-34}}{4\times 3.14}\)
\(∆P= 5.27 × 10^{-25}\)
Fractional uncertainty \( = \frac{\Delta P}{P}\)
\(\frac{\Delta P}{P}\)=\(\frac{5.27\times 10^{-25}}{10^{-20}}\)
\(=5.27 × 10^-5\)
Question
A student measures the radius R of a circular plate to determine its area. The absolute uncertainty in R is ΔR.
What is the fractional uncertainty in the area of the plate?
A \(\frac{2\Delta R}{R}\)
B \((\frac{\Delta R}{R})^2\)
C \(\frac{2\pi \Delta R}{R}\)
D \(\pi (\frac{\Delta R}{R})^2\)
▶️Answer/Explanation
Ans: A
For calculating approximate uncertainty we proceed as follows:
We know that Area \(A=\pi R^2\)
Taking natural log on both sides we get
\(ln A=ln(\pi \times r^2)\)
\(ln A= ln \pi + 2ln r\)
From Theory of errors we can write it as
\(\frac{\Delta A}{A} =\frac{2\Delta r}{r}\)
where \(\Delta A\) is uncertainty in A and \(\Delta r\) is uncertainty in r , there being no uncertainty in constant \(\pi\)
Question
A student is verifying the equation
\(x=\frac{2\lambda y}{z}\)
The percentage uncertainties are:
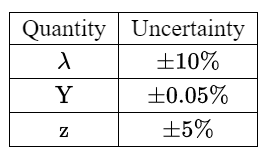
What is the percentage uncertainty in x?
A $5 \%$
B. $15 \%$
C. $25 \%$
D. $30 \%$
▶️Answer/Explanation
Ans: B

Hence percentage uncertainty in x = 10+5+0.05 = 15 %
